Физика
Круговой процесс (цикл) всегда состоит из нескольких процессов, в том числе и изопроцессов.
Согласно первому началу термодинамики, в каждом из таких процессов газом может совершаться работа и может изменяться его внутренняя энергия. Теплота, полученная или отданная газом в каждом процессе, будет различной.
В таблице отражены расчетные формулы, условные обозначения и нулевые значения для работы, изменения внутренней энергии и теплоты, полученной газом в некоторых процессах.
|
Название процесса |
Работа, совершенная газом, A |
Изменение внутренней энергии газа, ΔU |
Количество теплоты, полученной газом, Q = A + ΔU |
|---|---|---|---|
| Изотермический T = const |
A
T
A = νRTln(V2/V1) | 0 | A T |
| Изохорный V = const | 0 | ||
| Изобарный p = const | νR∆T, p∆V | , | , |
| Адиабатный Q = 0 | 0 |
При решении задач на вычисление коэффициента полезного действия произвольного цикла следует использовать следующий алгоритм:
1) построить график кругового процесса в координатах p(V);
2) выделить участки, соответствующие изопроцессам;
3) заполнить таблицу:
| Номер участка | Название процесса | Работа, совершенная газом, A | Изменение внутренней энергии газа, ΔU | Количество теплоты, полученной газом, Q = A + ΔU | Знак теплоты (+ или –) |
|---|---|---|---|---|---|
| 1–2 | |||||
| 2–3 | |||||
| (n − 1) − n | |||||
| n − 1 |
4) проанализировать, положительным или отрицательным является выражение для теплоты, полученной/отданной газом, в каждом процессе (в последней колонке таблицы указать соответствующий знак):
- газ получает теплоту, если Q > 0;
- газ отдает теплоту, если Q < 0;
5) рассчитать работу газа за цикл, суммируя алгебраически работы газа на каждом из участков (т.е. складывая значения работ из третьей колонки таблицы с учетом соответствующего знака):
A = A 12 + A 23 + ... + A n1 ;
6) найти теплоту, полученную газом за цикл Q получ, суммируя только те значения Q, которые являются положительными;
7) рассчитать коэффициент полезного действия для рассмотренного цикла по формуле
.
Пример 12. Идеальный одноатомный газ в идеальной тепловой машине совершает циклический процесс, состоящий из двух изохор и двух изобар. Максимальное давление газа в 4,00 раза больше минимального. Максимальный объем газа в 6,00 раз больше минимального. Определить коэффициент полезного действия идеальной тепловой машины.
Решение. На рисунке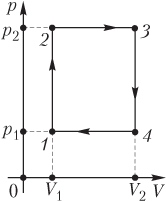
1–2 — изохора (V 1 = const);
2–3 — изобара (p 2 = const);
3–4 — изохора (V 2 = const);
4–1 — изобара (p 1 = const).
Коэффициент полезного действия цикла 1–2–3–4–1, изображенного на рисунке, определяется формулой
,
где A 12 — работа, совершаемая газом на участке 1–2; A 23 — работа, совершаемая газом на участке 2–3; A 34 — работа, совершаемая газом на участке 3–4; A 41 — работа, совершаемая газом на участке 4–1; Q получ — количество теплоты, полученной газом за цикл.
Запишем первое начало термодинамики для каждого участка:
- участок 1–2 (изохора) —
Q 12 = A 12 + ∆U 12 ,
где A 12 — работа газа при изохорном процессе на участке 1–2, A 12 = 0; ΔU 12 — изменение внутренней энергии газа на участке 1–2, ∆U 12 = = 1,5νR(T 2 − T 1); ν — количество вещества (газа); R — универсальная газовая постоянная; T 1 — начальная температура газа на участке 1–2; T 2 — конечная температура газа на участке 1–2;
- участок 2–3 (изобара) —
Q 23 = A 23 + ∆U 23 ,
где A 23 — работа газа при изобарном процессе на участке 2–3, A 23 = p 2(V 2 − V 1); p 2 — давление газа на участке 2–3; V 1 — начальный объем газа на участке 2–3; V 2 — конечный объем газа на участке 2–3; ΔU 23 — изменение внутренней энергии газа на участке 2–3, ∆U 23 = = 1,5νR(T 3 − T 2); T 2 — начальная температура газа на участке 2–3; T 3 — конечная температура газа на участке 2–3;
- участок 3–4 (изохора) —
Q 34 = A 34 + ∆U 34 ,
где A 34 — работа газа при изохорном процессе на участке 3–4, A 34 = 0; ΔU 34 — изменение внутренней энергии газа на участке 3–4, ∆U 34 = = 1,5νR(T 4 − T 3); T 3 — начальная температура газа на участке 3–4; T 4 — конечная температура газа на участке 3–4;
- участок 4–1 (изобара) —
Q 41 = A 41 + ∆U 41 ,
где A 41 — работа газа при изобарном процессе на участке 4–1, A 41 = p 1(V 1 − V 2); p 1 — давление газа на участке 4–1; V 2 — начальный объем газа на участке 4–1; V 1 — конечный объем газа на участке 4–1; ΔU 41 — изменение внутренней энергии газа на участке 4–1, ∆U 41 = = 1,5νR(T 1 − T 4); T 4 — начальная температура газа на участке 4–1; T 1 — конечная температура газа на участке 4–1.
Газ получает теплоту на участках 1–2 и 2–3, так как именно на этих участках количество теплоты является положительным. Следовательно, полученное за цикл количество теплоты определяется формулой
.
После преобразований получим
.
Коэффициент полезного действия цикла
.
Запишем уравнение Менделеева — Клапейрона для состояний идеального газа, обозначенных на графике точками 1 и 3:
p 1V 1 = νRT 1, p 2V 2 = νRT 3.
В выражении для коэффициента полезного действия произведем соответствующую замену, раскроем скобки и приведем подобные слагаемые:
.
Выполним почленное деление числителя и знаменателя на произведение (p 1V 1):
.
С учетом того, что p 1 и V 1 являются минимальными значениями давления и объема газа, а p 2 и V 2 — максимальными, выполним подстановку:
p 2 = 4,00p 1, V 2 = 6,00V 1.
Искомый коэффициент полезного действия составит
.
Пример 13. Рабочим веществом идеальной тепловой машины является идеальный одноатомный газ. Коэффициент полезного действия цикла 1–2–3–1 равен 30 %, а коэффициент полезного действия цикла 1–3–4–1 равен 40 %. Определить коэффициент полезного действия тепловой машины, работающей по циклу 1–2–3–4–1.
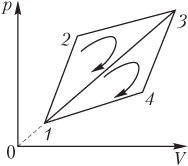
Решение. 1. Коэффициент полезного действия цикла 1–2–3–4–1 определяется формулой
,
где A 12 — работа, совершаемая газом на участке 1–2; A 23 — работа, совершаемая газом на участке 2–3; A 34 — работа, совершаемая газом на участке 3–4; A 41 — работа, совершаемая газом на участке 4–1; Q получ — количество теплоты, полученной газом за цикл.
Запишем первое начало термодинамики для каждого участка:
- участок 1–2 —
Q 12 = A 12 + ∆U 12 = A 12 + 1,5νR(T 2 − T 1) > 0,
где ΔU 12 — изменение внутренней энергии газа на участке 1–2, ∆U 12 = = 1,5νR(T 2 − T 1); ν — количество вещества (газа); R — универсальная газовая постоянная; T 1 — начальная температура газа на участке 1–2; T 2 — конечная температура газа на участке 1–2;
- участок 2–3 —
Q 23 = A 23 + ∆U 23 = A 23 + 1,5νR(T 3 − T 2) > 0,
где ΔU 23 — изменение внутренней энергии газа на участке 2–3, ∆U 23 = = 1,5νR(T 3 − T 2); T 2 — начальная температура газа на участке 2–3; T 3 — конечная температура газа на участке 2–3;
- участок 3–4 —
Q 34 = A 34 + ∆U 34 = A 34 + 1,5νR(T 4 − T 3) < 0,
где ΔU 34 — изменение внутренней энергии газа на участке 3–4; ∆U 34 = = 1,5νR(T 4 − T 3); T 3 — начальная температура газа на участке 3–4; T 4 — конечная температура газа на участке 3–4;
- участок 4–1 —
Q 41 = A 41 + ∆U 41 = A 41 + 1,5νR(T 1 − T 4) < 0,
где ΔU 41 — изменение внутренней энергии газа на участке 4–1, ∆U 41 = = 1,5νR(T 1 − T 4); T 4 — начальная температура газа на участке 4–1; T 1 — конечная температура газа на участке 4–1.
Газ получает теплоту на участках 1–2 и 2–3, так как Q 12 и Q 23 являются положительными. Следовательно, полученное за цикл количество теплоты определяется формулой
.
После преобразований имеем:
Q получ = A 12 + A 23 + 1,5νR(T 3 − T 1).
Коэффициент полезного действия цикла
.
Установим связь входящих в формулу величин с коэффициентами полезного действия на участках 1–2–3–1 и 1–3–4–1.
2. Коэффициент полезного действия тепловой машины, работающей по циклу 1–2–3–1.
Запишем первое начало термодинамики для каждого участка:
- участок 1–2 —
;
- участок 2–3 —
;
- участок 3–1 —
,
где ΔU 31 — изменение внутренней энергии газа на участке 3–1, ∆U 31 = = 1,5νR(T 1 − T 3); T 3 — начальная температура газа на участке 3–1; T 1 — конечная температура газа на участке 3–1.
Коэффициент полезного действия цикла 1–2–3–1:
.
3. Коэффициент полезного действия тепловой машины, работающей по циклу 1–3–4–1.
Запишем первое начало термодинамики для каждого участка:
- участок 1–3 —
,
где ΔU 13 — изменение внутренней энергии газа на участке 1–3, ∆U 13 = = 1,5νR(T 3 − T 1); T 1– начальная температура газа на участке 1–3; T 3 — конечная температура газа на участке 1–3;
- участок 3–4 —
;
- участок 4–1 —
.
Коэффициент полезного действия цикла 1–3–4–1:
.
Выражения для КПД образуют систему:
которую необходимо решить относительно η.
Из второго уравнения системы следует
,
а из третьего —
,
где η1 и η2 представлены в долях.
Подставим полученные уравнения в первое уравнение системы и преобразуем выражение
.
С учетом
A 13 = −A 31
получим
.
Вычислим:
.
КПД тепловой машины, работающей по циклу 1–2–3–4–1, составляет 58 %.










