Репетитор-онлайн — подготовка к ЦТ

6.3. Второй закон термодинамики

6.3.1. Коэффициент полезного действия тепловых двигателей. Цикл Карно

Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.

Рис. 6.3

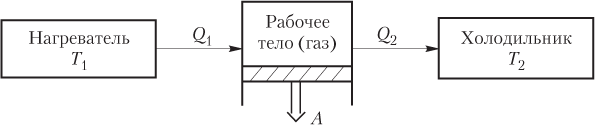
Цикл работы теплового двигателя состоит из трех этапов:

1) нагреватель передает газу количество теплоты Q ₁;

2) газ, расширяясь, совершает работу A;

3) для возвращения газа в исходное состояние холодильнику передается теплота Q ₂.

Из первого закона термодинамики для циклического процесса

Q = A,

где Q — количество теплоты, полученное газом за цикл, Q = Q ₁ − Q ₂; Q ₁ — количество теплоты, переданное газу от нагревателя; Q ₂ — количество теплоты, отданное газом холодильнику.

Поэтому для идеальной тепловой машины справедливо равенство

Q ₁ − Q ₂ = A.

Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии

Q ₁ = A + Q ₂,

где Q ₁ — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q ₂ — теплота, переданная газом холодильнику.

Коэффициент полезного действия тепловой машины вычисляется по одной из формул:

$η = \frac{A}{Q_{1}} \cdot 100 %$ , $η = \frac{Q_{1} - Q_{2}}{Q_{1}} \cdot 100 %$ , $η = (1 - \frac{Q_{2}}{Q_{1}}) \cdot 100 %$ ,

где A — работа, совершенная газом; Q ₁ — теплота, переданная от нагревателя рабочему телу (газу); Q ₂ — теплота, переданная газом холодильнику.

Наиболее часто в тепловых машинах используется цикл Карно, так как он является самым экономичным.

Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.

Рис. 6.4

Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q ₁ и происходит изотермическое расширение газа при температуре нагревателя T ₁. Газ совершает положительную работу (A ₁₂ > 0), его внутренняя энергия не изменяется (∆U ₁₂ = 0).

Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A ₂₃ приводит к уменьшению внутренней энергии газа: ∆U ₂₃ = −A ₂₃, газ охлаждается до температуры холодильника T ₂.

Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q ₂ и происходит изотермическое сжатие газа при температуре холодильника T ₂. Газ совершает отрицательную работу (A ₃₄ < 0), его внутренняя энергия не изменяется (∆U ₃₄ = 0).

Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A ₄₁ приводит к увеличению внутренней энергии газа: ∆U ₄₁ = −A ₄₁, газ нагревается до температуры нагревателя T ₁, т.е. возвращается в исходное состояние.

Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:

$η = \frac{T_{1} - T_{2}}{T_{1}} \cdot 100 %$ , $η = (1 - \frac{T_{2}}{T_{1}}) \cdot 100 %$ ,

где T ₁ — температура нагревателя; T ₂ — температура холодильника.

Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?

Решение. Коэффициент полезного действия тепловой машины определяется формулой

$η = \frac{A}{Q_{1}} \cdot 100 %$ ,

где A — работа, совершаемая газом за цикл; Q ₁ — количество теплоты, которое передается от нагревателя рабочему телу (газу).

Искомой величиной является количество теплоты Q ₂, переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.

Связь между работой A, теплотой Q ₁, переданной от нагревателя газу, и искомой величиной Q ₂ устанавливается с помощью закона сохранения энергии для идеальной тепловой машины

Q ₁ = A + Q ₂.

Уравнения образуют систему

$\begin{array}{l} η = \frac{A}{Q_{1}} \cdot 100 %, \\ Q_{1} = A + Q_{2}, \end{array}}$

которую необходимо решить относительно Q ₂.

Для этого исключим из системы Q ₁, выразив из каждого уравнения

$\begin{array}{l} Q_{1} = \frac{A}{η} \cdot 100 %, \\ Q_{1} = A + Q_{2} \end{array}}$

и записав равенство правых частей полученных выражений:

$\frac{A}{η} \cdot 100 % = A + Q_{2}$ .

Искомая величина определяется равенством

$Q_{2} = \frac{A}{η} \cdot 100 % - A = A (\frac{100 %}{η} - 1)$ .

Расчет дает значение:

$Q_{2} = 400 \cdot (\frac{100 %}{40 %} - 1) = 600$ Дж.

Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.

Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.

Решение. Для расчета коэффициента полезного действия воспользуемся формулой

$η = (1 - \frac{Q_{2}}{Q_{1}}) \cdot 100 %$ ,

где Q ₂ — количество теплоты, которое передается за цикл от газа холодильнику; Q ₁ — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).

Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t:

$η = (1 - \frac{Q_{2} / t}{Q_{1} / t}) \cdot 100 %$ ,

где Q ₂/t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q ₁/t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).

В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:

от нагревателя газу —

$\frac{Q_{1}}{t} = 122 кДж/мин = \frac{122 \cdot 10^{3}}{60} Дж/с$ ;

от газа холодильнику —

$\frac{Q_{2}}{t} = 30,5 кДж/мин = \frac{30,5 \cdot 10^{3}}{60} Дж/с$ .

Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:

$η = (1 - \frac{30,5 \cdot 10^{3}}{60} \cdot \frac{60}{122 \cdot 10^{3}}) \cdot 100 % = 75 %$ .

Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?

Решение. Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:

до изменения температур нагревателя и холодильника —

$η_{1} = (1 - \frac{T_{2}}{T_{1}}) \cdot 100 %$ ,

где T ₁ — первоначальная температура нагревателя; T ₂ — первоначальная температура холодильника;

после изменения температур нагревателя и холодильника —

$η_{2} = (1 - \frac{{T^{'}}_{2}}{{T^{'}}_{1}}) \cdot 100 %$ ,

где ${T^{'}}_{1}$ — новая температура нагревателя, ${T^{'}}_{1} = 1,2 T_{1}$ ; ${T^{'}}_{2}$ — новая температура холодильника, ${T^{'}}_{2} = 0,8 T_{2}$ .

Уравнения для коэффициентов полезного действия образуют систему

$\begin{array}{l} η_{1} = (1 - \frac{T_{2}}{T_{1}}) \cdot 100 %, \\ η_{2} = (1 - \frac{0,8 T_{2}}{1,2 T_{1}}) \cdot 100 %, \end{array}}$

которую необходимо решить относительно η₂.

Из первого уравнения системы с учетом значения η₁ = 25 % найдем отношение температур

$\frac{T_{2}}{T_{1}} = 1 - \frac{η_{1}}{100 %} = 1 - \frac{25 %}{100 %} = 0,75$

и подставим во второе уравнение

$η_{2} = (1 - \frac{0,8}{1,2} \cdot 0,75) \cdot 100 % = 50 %$ .

Искомое отношение коэффициентов полезного действия равно:

$\frac{η_{2}}{η_{1}} = \frac{50 %}{25 %} = 2,0$ .

Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.

Физика