Физика
Система тел может обладать как кинетической, так и потенциальной энергией.
Полная механическая энергиятела представляет собой сумму его кинетической и потенциальной энергий:
E = Wk+ Wp,
где Wk — кинетическая энергия тела; Wp — потенциальная энергия тела.
Полная механическая энергия системы нескольких тел представляет собой сумму полных механических энергий всех тел системы:
E = E1+ E2+ ... + EN,
где E1 — полная механическая энергия первого тела; E2 — полная механическая энергия второго тела и т.д.
Полная механическая энергия системы нескольких тел является суммой кинетических и потенциальных энергий каждого тела, входящего в данную систему:
E = Ek+ Ep,
где Ek — сумма кинетических энергий всех тел системы (кинетическая энергия системы); Ep — сумма потенциальных энергий всех тел системы (потенциальная энергия системы).
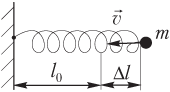
Пример 28. Груз массой 0,50 кг, прикрепленный к пружине жесткостью 0,10 кН/м, совершает колебания в горизонтальной плоскости. Вычислить полную механическую энергию системы пружина — груз в момент времени, когда пружина растянута на 10 см, а закрепленный на ее конце груз имеет скорость 2,0 м/с.
Решение. Полная механическая энергия системы пружина — груз является суммой потенциальной энергии пружины и кинетической энергии груза:
E = Wk+ Wp,
где Wp — потенциальная энергия деформированной пружины; Wk — кинетическая энергия груза.
На рисунке изображена система пружина — груз, показаны направление скорости движения груза и величина растяжения пружины ∆l.
Значения потенциальной энергии пружины и кинетической энергии груза определяются формулами:
- потенциальная энергия деформированной пружины
;
- кинетическая энергия движущегося груза
,
где k — коэффициент жесткости пружины; ∆l — величина деформации (растяжения) пружины; m — масса груза; v — величина скорости груза.
Подстановка записанных формул для Wp и Wk в исходное выражение дает формулу для расчета полной механической энергии системы пружина — груз в указанный момент времени:
.
Произведем вычисление:
Дж.
Пример 29. Тело массой 1,0 кг брошено с поверхности Земли с начальной скоростью 20 м/с под углом 30° к горизонту. Найти полную механическую энергию тела относительно поверхности Земли через 2,0 секунды полета. Сопротивлением воздуха пренебречь.
Решение. Полная механическая энергия тела является суммой потенциальной энергии тела относительно поверхности Земли и его кинетической энергии:
E = Wk+ Wp,
где Wk — кинетическая энергия; Wp — потенциальная энергия тела.
На рисунке изображена траектория движения тела, показаны направления скорости его движения и выбранная система координат.
Значения потенциальной и кинетической энергии тела определяются формулами:
- потенциальная энергия
Wp = mgh;
- кинетическая энергия
,
где m — масса тела; g — модуль ускорения свободного падения; h — высота тела над поверхностью Земли в указанный момент времени; v — модуль скорости тела.
- Для расчета кинетической энергии тела необходимо вычислить величину скорости тела в указанный момент времени. Расчет произведем по формуле
,
где vx — проекция скорости тела на ось Ox; vy — проекция скорости тела на ось Oy.
Проекции скорости определяются выражениями
где v0 — модуль начальной скорости тела; t0 = 2,0 с — момент времени, в который определяется значение полной энергии тела.
Подстановка полученных значений в выражение для вычисления модуля скорости дает ее значение:
м/с.
- Для расчета потенциальной энергии тела необходимо вычислить высоту подъема тела над поверхностью Земли в указанный момент времени:
м,
т.е. в указанный момент времени тело упало на Землю.
Подставим найденные значения скорости и высоты подъема в исходное уравнение для расчета полной энергии и выполним расчет:
кДж.
Нетрудно заметить, что найденное значение полной механической энергии тела в указанный момент времени совпадает со значением полной механической энергии в начальный момент времени:
Дж.
Однако равенство
E = E0
имеет место только в отсутствие сопротивления воздуха.