Предметы

Физика

Законы сохранения

3.4. Механическая энергия

3.4.2. Потенциальная энергия

Теория Тренинг

Физика

Общий тест

3.4. Механическая энергия

3.4.2. Потенциальная энергия

Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.

Потенциальная энергия деформированной пружины

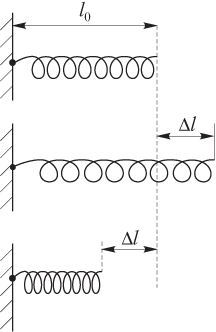
Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенциальной энергией, которая определяется формулой

$W_{p} = \frac{k {(Δ l)}^{2}}{2}$ ,

где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).

Рис. 3.7

Потенциальная энергия недеформированной пружины равна нулю.

Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.

В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).

Потенциальная энергия взаимодействия тела и Земли

Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой

W_p = mgh + C,

где m — масса тела; g — модуль ускорения свободного падения.

Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.

Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.

В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).

Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.

Решение. Потенциальная энергия составной пружины определяется формулой

$W_{p} = \frac{k_{общ} {(Δ l)}^{2}}{2}$ ,

где k_общ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.

Коэффициент жесткости составной пружины определяется по-разному:

для N одинаковых пружин, соединенных последовательно,

$k_{общ 1} = \frac{k_{0}}{N}$ ;

для N одинаковых пружин, соединенных параллельно,

k_общ2 = Nk₀,

где k₀ — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.

Потенциальная энергия составной пружины вычисляется по формулам:

для N одинаковых пружин, соединенных последовательно,

$W_{p 1} = \frac{k_{общ 1} {(Δ l)}^{2}}{2} = \frac{k_{0} {(Δ l)}^{2}}{2 N}$ ;

для N одинаковых пружин, соединенных параллельно,

$W_{p 2} = \frac{k_{общ 2} {(Δ l)}^{2}}{2} = \frac{N k_{0} {(Δ l)}^{2}}{2}$ .

Отношение потенциальных энергий

$\frac{W_{p 1}}{W_{p 2}} = \frac{k_{0} {(Δ l)}^{2}}{2 N} \frac{2}{N k_{0} {(Δ l)}^{2}} = \frac{1}{N^{2}}$

определяется только количеством пружин и не зависит от деформации составной пружины.

Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,

соединенных последовательно:

$W_{p 1} = \frac{k_{0} {(Δ l)}^{2}}{2 N} = \frac{1,0 \cdot 10^{3} {(10 \cdot 10^{- 2})}^{2}}{2 \cdot 2} = 2,5$ Дж;

соединенных параллельно:

$W_{p 2} = \frac{N k_{0} {(Δ l)}^{2}}{2} = \frac{2 \cdot 1,0 \cdot 10^{3} {(10 \cdot 10^{- 2})}^{2}}{2} = 10$ Дж.

Отношение указанных потенциальных энергий равно

$\frac{W_{p 1}}{W_{p 2}} = \frac{1}{N^{2}} = \frac{1}{2^{2}} = 4$ .

Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.

Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.

Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой

W_p = mgh,

где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.

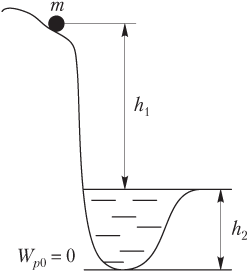
Выберем нулевой уровень потенциальной энергии (W_p = 0) на дне озера так, как показано на рисунке.

Тогда высота, на которую поднято тело над указанным уровнем, является суммой:

h = h₁ + h₂,

где h₁ = 1,50 км — высота горы; h₁ = 250 м — глубина озера.

Потенциальная энергия тела относительно дна озера определяется выражением

W_p = mg(h₁ + h₂).

Расчет дает значение:

$W_{p} = 500 \cdot 10^{- 3} \cdot 10 \cdot (1,50 + 0,25) \cdot 10^{3} = 8,75 \cdot 10^{3} Дж = 8,75$ кДж.