Предметы

Физика

Законы сохранения

3.4. Механическая энергия

3.4.1. Кинетическая энергия

Теория Тренинг

Физика

Общий тест

3.4. Механическая энергия

3.4.1. Кинетическая энергия

Кинетическая энергия — это энергия механического движения некоторой системы тел. Кинетической энергией обладают только движущиеся тела.

В Международной системе единиц кинетическая энергия движущегося тела измеряется в джоулях (1 Дж).

Кинетическая энергия поступательного движения тела определяется формулой

$W_{k} = \frac{m v^{2}}{2}$ ,

где m — масса движущегося тела; v — модуль его скорости.

Для расчета кинетической энергии при поступательном движении тела существует еще одна формула:

$W_{k} = \frac{P^{2}}{2 m}$ ,

где P = mv — модуль импульса движущегося тела.

Кинетическая энергия вращательного движения тела определяется формулой

$W_{k} = \frac{m ω^{2} R^{2}}{2}$ ,

где m — масса движущегося тела; ω — величина угловой скорости (циклическая частота); R — радиус окружности, по которой движется тело.

Для расчета кинетической энергии при вращательном движении тела существует еще одна формула:

$W_{k} = 2 m π^{2} ν^{2} R^{2}$ ,

где ν — частота вращения тела.

При решении задач на расчет кинетической энергии системы тел полезно помнить, что она складывается из кинетических энергий каждого из тел:

$W_{k сис} = W_{k 1} + W_{k 2} + ... + W_{k N}$ ,

где W_k₁, W_k₂, ..., W_kN — кинетические энергии каждого тела.

При решении задач на расчет кинетической энергии вращательного движения могут оказаться полезными следующие формулы:

связь между линейной v и угловой ω скоростями:

v = ωR,

где R — радиус окружности по которой движется тело;

связь между циклической частотой ω и частотой ν:

ω = 2πν;

связь между циклической частотой ω (или частотой ν) и периодом обращения тела по окружности T:

ωT = 2π или $ν = \frac{1}{T}$ .

Пример 24. Координата тела, движущегося вдоль оси Ox, зависит от времени по закону x(t) = 8,0 − 2,0t + t², где координата задана в метрах, время — в секундах. Определить изменение кинетической энергии тела с начала третьей до конца четвертой секунды движения. Масса тела составляет 3,0 кг.

Решение. Кинетическая энергия тела определяется формулами:

в начале третьей секунды движения (t₁ = 2 c)

$W_{k 1} = \frac{m v^{2} (t_{1})}{2}$ ;

в конце четвертой секунды движения (t₂ = 4 c)

$W_{k 2} = \frac{m v^{2} (t_{2})}{2}$ ,

где v(t₁) — модуль скорости тела в начале третьей секунды; v(t₂) — модуль скорости тела в конце четвертой секунды.

Уравнение движения тела

$x (t) = 8,0 - 2,0 t + t^{2}$

позволяет установить закон изменения проекции скорости на ось Ox с течением времени в виде:

$v_{x} (t) = v_{0 x} + a_{x} t$ ,

где v₀_x = −2,0 м/с — проекция начальной скорости на ось Ox; a_x = = 2,0 м/с² — проекция ускорения на указанную ось.

Таким образом, зависимость проекции скорости от времени, записанная в явном виде

$v_{x} (t) = - 2,0 + 2,0 t$ ,

позволяет получить соответствующие проекции скоростей:

в начале третьей секунды движения (t₁ = 2 c)

$v_{x} (t_{1}) = - 2,0 + 2,0 t_{1} = - 2,0 + 2,0 \cdot 2 = 2,0$ м/с;

в конце четвертой секунды движения (t₂ = 4 c)

$v_{x} (t_{2}) = - 2,0 + 2,0 t_{2} = - 2,0 + 2,0 \cdot 4 = 6,0$ м/с.

Значения кинетической энергии тела в указанные моменты времени:

в начале третьей секунды движения (t₁ = 2 c)

$W_{k 1} = \frac{3,0 \cdot {(2,0)}^{2}}{2} = 6,0$ Дж,

в конце четвертой секунды движения (t₂ = 4 c)

$W_{k 2} = \frac{3,0 \cdot {(6,0)}^{2}}{2} = 54$ Дж.

Искомая разность кинетических энергий составляет

$Δ W_{k} = W_{k 2} - W_{k 1} = 54 - 6,0 = 48$ Дж.

Таким образом, кинетическая энергия тела за указанный интервал времени возросла на 48 Дж.

Пример 25. Тело движется в плоскости xOy по траектории вида x² + y² = 25 под действием центростремительной силы, величина которой равна 50 Н. Масса тела составляет 2,0 кг. Координаты x и y заданы в метрах. Найти кинетическую энергию тела.

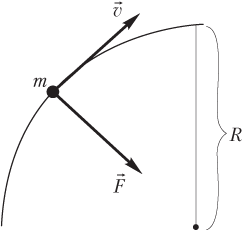
Решение. Траектория движения тела представляет собой окружность радиусом 5,0 м. Согласно условию задачи, на тело действует только одна сила, направленная к центру этой окружности.

Модуль указанной силы является постоянной величиной, поэтому тело обладает постоянным центростремительным ускорением, не влияющим на величину скорости тела; следовательно, тело движется по окружности с постоянной скоростью.

Рисунок иллюстрирует данное обстоятельство.

Величина центростремительной силы определяется формулой

$F_{ц . с} = \frac{m v^{2}}{R}$ ,

где m — масса тела; v — модуль скорости тела; R — радиус окружности, по которой движется тело.

Выражение для кинетической энергии тела имеет вид:

$W_{k} = \frac{m v^{2}}{2}$ .

Отношение уравнений

$\frac{F_{ц . с}}{W_{k}} = \frac{m v^{2}}{R} \frac{2}{m v^{2}} = \frac{2}{R}$

позволяет получить формулу для расчета искомой кинетической энергии:

$W_{k} = \frac{F_{ц . с} R}{2}$

и рассчитать ее значение:

$W_{k} = \frac{50 \cdot 5,0}{2} = 125$ Дж.