Физика

Общий тест

1.4. Относительность движения

1.4.2. Применение закона сложения скоростей к задачам о пересечении реки

При решении задач на относительность прямолинейного движения наибольшую трудность вызывают задачи о перемещении пловца через реку на противоположный берег. Аналогичные трудности при решении задач на относительность криволинейного движения возникают при рассмотрении движения колеса по горизонтальной поверхности.

При решении задач о пересечении реки пловцом и т.п. необходимо учитывать, что берег считается неподвижной системой отсчета, вода — подвижной; скорость воды в реке относительно берега $\vec{u}$ направлена параллельно берегу.

Если формулировка условия задачи предполагает, что пловец пересекает реку определенным образом с какой-то скоростью, то указанная скорость задана относительно берега:

скорость пловца относительно берега обозначается $\vec{v}$ (рис. 1.36);

Рис. 1.36

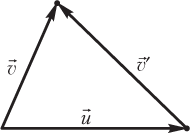
скорость пловца относительно воды находят по формуле (рис. 1.37)
${\vec{v}}^{'} = \vec{v} - \vec{u}$ ,
где $\vec{u}$ — скорость воды в реке; $\vec{v}$ и ${\vec{v}}^{'}$ — скорости пловца (лодки и т.п.) относительно берега и воды соответственно.

Рис. 1.37

Если формулировка условия задачи предполагает, что пловец, корабль, лодка и т.п. держит курс такой-то с определенной скоростью, то указанная скорость задана относительно воды:

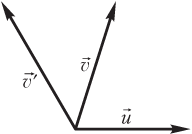
скорость пловца относительно воды обозначается ${\vec{v}}^{'}$ (рис. 1.38);

Рис. 1.38

скорость пловца относительно берега находят по формуле (рис. 1.39)
$\vec{v} = {\vec{v}}^{'} + \vec{u}$ ,
где $\vec{u}$ — скорость воды в реке; $\vec{v}$ и ${\vec{v}}^{'}$ — скорости пловца (лодки и т.п.) относительно берега и воды соответственно.

Рис. 1.39

Пример 27. Лодка движется со скоростью 6,0 м/с относительно воды в реке под углом 45° к течению, скорость которого 2,0 м/с. Определить модуль скорости лодки относительно берега.

Решение. Подвижной системой отсчета является вода, ее скорость обозначим $\vec{u}$ .

Скорость лодки относительно подвижной системы отсчета (относительно воды) обозначим ${\vec{v}}^{'}$ .

Запишем закон сложения скоростей в виде:

$\vec{v} = {\vec{v}}^{'} + \vec{u}$

и построим «треугольник скоростей», как показано на рисунке.

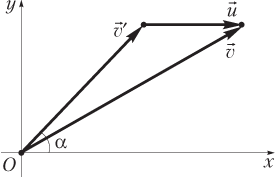
Искомой скоростью является скорость лодки $\vec{v}$ относительно неподвижной системы отсчета (берега). Для определения модуля указанной скорости запишем закон сложения скоростей в проекциях на координатные оси:

$\begin{array}{l} v_{x} = {v^{'}}_{x} + u_{x}, \\ v_{y} = {v^{'}}_{y} + u_{y}, \end{array}}$

или в явном виде:

$\begin{array}{l} v_{x} = v^{'} \cos 45 ° + u, \\ v_{y} = v^{'} \sin 45 ° . \end{array}}$ .

Вычислим значения проекций искомой скорости:

$\begin{array}{l} v_{x} = 6,0 \cdot 0,5 \sqrt{2} + 2,0 = (3,0 \sqrt{2} + 2,0) м/с, \\ v_{y} = 6,0 \cdot 0,5 \sqrt{2} = (3,0 \sqrt{2}) м/с . \end{array}}$ .

Модуль скорости лодки относительно берега рассчитаем по формуле

$v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{{(3,0 \sqrt{2} + 2,0)}^{2} + {(3,0 \sqrt{2})}^{2}} \approx 7,5$ м/с.