Предметы

Физика

Кинематика

1.4. Относительность движения

1.4.1. Закон сложения перемещений и закон сложения скоростей

Теория Тренинг

Физика

Общий тест

1.4. Относительность движения

1.4.1. Закон сложения перемещений и закон сложения скоростей

Механическое движение одного и того же тела выглядит по-разному для разных систем отсчета.

Для определенности будем использовать две системы отсчета (рис. 1.33):

K — неподвижную систему отсчета;
K′ — подвижную систему отсчета.

Рис. 1.33

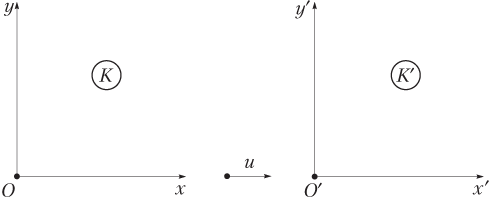
Система K′ движется относительно системы отсчета K в положительном направлении оси Ox со скоростью $\vec{u}$ .

Пусть в системе отсчета K материальная точка (тело) движется со скоростью $\vec{v}$ и за интервал времени ∆t совершает перемещение $Δ \vec{r}$ . Относительно системы отсчета K′ эта материальная точка имеет скорость ${\vec{v}}^{'}$ и за указанный интервал времени ∆t совершает перемещение $Δ \vec{r^{'}}$ .

Закон сложения перемещений

Перемещения материальной точки в неподвижной (K) и движущейся (K′) системах отсчета ( $Δ \vec{r}$ и $Δ \vec{r^{'}}$ соответственно) различаются между собой и связаны законом сложения перемещений:

$Δ \vec{r} = Δ \vec{r^{'}} + \vec{u} Δ t$ ,

где $Δ \vec{r}$ — перемещение материальной точки (тела) за интервал времени ∆t в неподвижной системе отсчета K; $Δ \vec{r^{'}}$ — перемещение материальной точки (тела) за интервал времени ∆t в движущейся системе отсчета K′; $\vec{u}$ — скорость системы отсчета K′, движущейся относительно системы отсчета K.

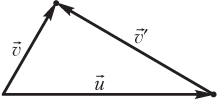
Закону сложения перемещений соответствует «треугольник перемещений» (рис. 1.34).

Рис. 1.34

Закон сложения перемещений при решении задач иногда целесообразно записывать в координатной форме:

$\begin{array}{l} Δ x = Δ x^{'} + u_{x} Δ t, \\ Δ y = Δ y^{'} + u_{y} Δ t, \end{array}}$

где ∆x и ∆y — изменение координат x и y материальной точки (тела) за интервал времени ∆t в системе отсчета K; ∆x′ и ∆y′ — изменение соответствующих координат материальной точки (тела) за интервал времени ∆t в системе отсчета K′; u_x и u_y — проекции скорости $\vec{u}$ системы отсчета K′, движущейся относительно системы отсчета K, на координатные оси.

Закон сложения скоростей

Скорости материальной точки в неподвижной (K) и движущейся (K′) системах отсчета ( $\vec{v}$ и ${\vec{v}}^{'}$ соответственно) также различаются между собой и связаны законом сложения скоростей:

$\vec{v} = {\vec{v}}^{'} + \vec{u}$ ,

где $\vec{u}$ — скорость системы отсчета K′, движущейся относительно системы отсчета K.

Закону сложения скоростей соответствует «треугольник скоростей» (рис. 1.35).

Рис. 1.35

Закон сложения скоростей при решении задач иногда целесообразно записывать в проекциях на координатные оси:

$\begin{matrix} v_{x} = {v^{'}}_{x} + u_{x}, \\ v_{y} = {v^{'}}_{y} + u_{y}, \end{matrix}}$

где v_x и v_y — проекции вектора скорости $\vec{v}$ материальной точки (тела) в системе отсчета K на координатные оси; ${v^{'}}_{x}$ и ${v^{'}}_{y}$ — проекции вектора скорости ${\vec{v}}^{'}$ материальной точки (тела) в системе отсчета K′ на координатные оси; u_x и u_y — проекции скорости $\vec{u}$ системы отсчета K′, движущейся относительно системы отсчета K, на координатные оси.

Относительная скорость движения двух тел

Для определения относительной скорости движения двух тел удобно пользоваться следующим алгоритмом:

1) выяснить, какое из тел считается системой отсчета; скорость этого тела обозначить как $\vec{u};$

2) скорость второго тела обозначить как $\vec{v}$ ;

3) относительную скорость тел обозначить как ${\vec{v}}^{'}$ ;

4) векторы $\vec{v}$ , ${\vec{v}}^{'}$ и $\vec{u}$ изобразить в системе координат xOy;

5) записать закон сложения скоростей в виде

$\vec{v} = {\vec{v}}^{'} + \vec{u}$ или $\begin{matrix} v_{x} = {v^{'}}_{x} + u_{x}, \\ v_{y} = {v^{'}}_{y} + u_{y}; \end{matrix}}$

6) выразить ${\vec{v}}^{'}$ :

${\vec{v}}^{'} = \vec{v} - \vec{u}$

или

{v^{'}}_{x}

{v^{'}}_{y}

$\begin{matrix} {v^{'}}_{x} = v_{x} - u_{x}, \\ {v^{'}}_{y} = v_{y} - u_{y}; \end{matrix}}$

7) найти модуль вектора относительной скорости ${\vec{v}}^{'}$ по формуле

$v^{'} = \sqrt{{v^{'}}_{x}^{2} + {v^{'}}_{y}^{2}}$ ,

Для определения относительной скорости движения двух тел, движущихся вдоль одной координатной оси, удобно пользоваться следующим алгоритмом:

1) выяснить, какое из тел считается системой отсчета; скорость этого тела обозначить как $\vec{u}$ ;

2) скорость второго тела обозначить как $\vec{v}$ ;

3) относительную скорость тел обозначить как ${\vec{v}}^{'}$ ;

4) векторы $\vec{v}$ , ${\vec{v}}^{'}$ и $\vec{u}$ изобразить на координатной оси Ox;

5) записать закон сложения скоростей в виде:

$v_{x} = {v^{'}}_{x} + u_{x}$ ;

6) выразить ${v^{'}}_{x}$ :

${v^{'}}_{x} = v_{x} - u_{x}$ ;

7) найти модуль вектора относительной скорости $\vec{v^{'}}$ по формуле

$v^{'} = | {v^{'}}_{x} |$ ,

Пример 26. Первое тело движется со скоростью 6,0 м/с в положительном направлении оси Ox, а второе — со скоростью 8,0 м/с в ее отрицательном направлении. Определить модуль скорости первого тела в системе отсчета, связанной со вторым телом.

Решение. Подвижной системой отсчета является второе тело; проекция скорости $\vec{u}$ подвижной системы отсчета на ось Ox равна:

u_x = −8,0 м/с,

так как движение второго тела происходит в отрицательном направлении указанной оси.

Первое тело относительно неподвижной системы отсчета имеет скорость $\vec{v}$ ; ее проекция на ось Ox равна:

v_x = 6,0 м/с,

так как движение первого тела происходит в положительном направлении указанной оси.

Закон сложения скоростей для решения данной задачи целесообразно записать в проекции на координатную ось, т.е. в следующем виде:

$v_{x} = {v^{'}}_{x} + u_{x}$ ,

где ${v^{'}}_{x}$ — проекция скорости первого тела относительно подвижной системы отсчета (второго тела).

Величина ${v^{'}}_{x}$ является искомой; ее значение определяется формулой

${v^{'}}_{x} = v_{x} - u_{x}$ .

Произведем вычисление:

${v^{'}}_{x} = 6,0 - (- 8,0) = 14$ м/с.

Пример 29. Спортсмены бегут друг за другом цепочкой длиной 46 м с одинаковой скоростью. Навстречу им бежит тренер со скоростью, втрое меньшей скорости спортсменов. Каждый спортсмен, поравнявшись с тренером, поворачивает и бежит назад с прежней скоростью. Какова станет длина цепочки, когда все спортсмены будут бежать в обратном направлении?

Решение. Пусть движение спортсменов и тренера происходит вдоль оси Ox, начало которой совпадает с положением последнего спортсмена. Тогда уравнения движения относительно Земли имеют следующий вид:

последнего спортсмена —
x₁(t) = vt;
тренера —
$x_{2} (t) = L - \frac{1}{3} v t$ ;
первого спортсмена —
x₃(t) = L − vt,
где v — модуль скорости каждого спортсмена; $\frac{1}{3} v$ — модуль скорости тренера; L — первоначальная длина цепочки; t — время.

Свяжем подвижную систему отсчета с тренером.

Уравнение движения последнего спортсмена относительно подвижной системы отсчета (тренера) обозначим x′(t) и найдем из закона сложения перемещений, записанного в координатной форме:

x(t) = x′(t) + X(t), т.е. x′(t) = x(t) − X(t),

где

$X (t) = x_{2} (t) = L - \frac{1}{3} v t$ —

уравнение движения тренера (подвижной системы отсчета) относительно Земли;

x(t) = x₁(t) = vt;

уравнение движения последнего спортсмена относительно Земли.

Подстановка выражений x(t), X(t) в записанное уравнение дает:

$x^{'} (t) = x_{1} (t) - x_{2} (t) = v t - (L - \frac{1}{3} v t) = \frac{4}{3} v t - L$ .

Данное уравнение представляет собой уравнение движения последнего спортсмена относительно тренера. В момент встречи последнего спортсмена и тренера (t = t₀) их относительная координата x′(t₀) обращается в ноль:

$\frac{4}{3} v t_{0} - L = 0$ .

Уравнение позволяет найти указанный момент времени:

$t_{0} = \frac{3 L}{4 v}$ .

В этот момент времени все спортсмены начинают бежать в противоположном направлении. Длина цепочки спортсменов определяется разностью координат первого x₃(t₀) и последнего x₁(t₀) спортсмена в указанный момент времени:

$l = | x_{3} (t_{0}) - x_{1} (t_{0}) |$ ,

или в явном виде:

$l = | (L - v t_{0}) - v t_{0} | = | L - 2 v t_{0} | = | L - 2 v \frac{3 L}{4 v} | = 0,5 L = 0,5 \cdot 46 = 23$ м.