Физика

Общий тест

1.4. Относительность движения

1.4.3. Применение закона сложения скоростей к задачам о качении колеса

При рассмотрении относительности криволинейного движения (задачи о движении колеса, велосипедиста, мотоциклиста и т.п.) необходимо учитывать, что Земля является неподвижной системой отсчета, центр колеса — подвижной; скорость центра колеса относительно Земли $\vec{u}$ совпадает со скоростью объекта (велосипедиста, мотоциклиста и т.п.) и направлена параллельно Земле в сторону его движения.

Скорость любой точки обода колеса относительно центра — это скорость ${\vec{v}}^{'}$ ; направление ${\vec{v}}^{'}$ совпадает с направлением касательной, проведенной в указанной точке (рис. 1.40), а ее модуль совпадает с модулем скорости центра относительно Земли (при условии, что движение колеса происходит без проскальзывания):

$v^{'} = u$ .

Рис. 1.40

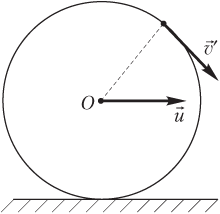
Скорость точки обода колеса относительно Земли находят, применяя закон сложения скоростей (рис. 1.41):

$\vec{v} = {\vec{v}}^{'} + \vec{u}$ .

Рис. 1.41

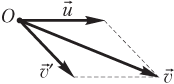
Иногда закон сложения скоростей целесообразно записывать в виде системы уравнений:

$\begin{matrix} v_{x} = {v^{'}}_{x} + u_{x} \\ v_{y} = {v^{'}}_{y} + u_{y}, \end{matrix}}$

где v_x, ${v^{'}}_{x}$ , u_x — проекции скоростей $\vec{v}$ , ${\vec{v}}^{'}$ , $\vec{u}$ на координатную ось Ox; v_y, ${v^{'}}_{y}$ , u_y — проекции соответствующих скоростей на координатную ось Oy.

Пример 28. Тонкий обруч катится без проскальзывания по горизонтальной поверхности. Скорость центра обруча относительно Земли равна 9,2 м/с. Определить относительно Земли модуль скорости точки обруча, для которой радиус составляет с горизонтом угол 30°.

Решение. Подвижной системой отсчета является центр обруча, его скорость обозначим $\vec{u}$ . Скорость указанной точки обруча относительно подвижной системы отсчета (центра обруча) обозначим ${\vec{v}}^{'}$ .

Запишем закон сложения скоростей в виде:

$\vec{v} = {\vec{v}}^{'} + \vec{u}$

и построим «треугольник скоростей», как показано на рисунке.

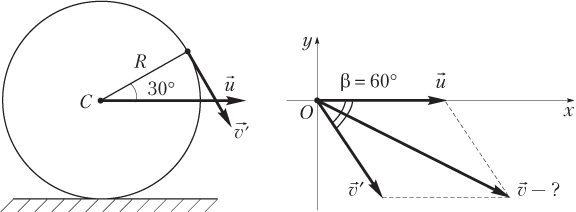
Искомой скоростью является скорость указанной точки обруча $\vec{v}$ относительно неподвижной системы отсчета (Земли).

Следует отметить, что движение обруча происходит без проскальзывания. Поэтому модуль скорости любой точки обруча относительно его центра v′ совпадает с модулем скорости центра обруча относительно Земли u:

v′ = u.

Для определения модуля скорости указанной точки обруча относительно Земли $\vec{v}$ запишем закон сложения скоростей в проекциях на координатные оси:

$\begin{matrix} v_{x} = {v^{'}}_{x} + u_{x}, \\ v_{y} = {v^{'}}_{y} + u_{y}, \end{matrix}}$

или в явном виде:

$\begin{array}{l} v_{x} = v^{'} \cos 60 ° + u = u \cos 60 ° + u = u (\cos 60 ° + 1), \\ v_{y} = - v^{'} \sin 60 ° = - u \sin 60 ° . \end{array}}$

Вычислим значения проекций искомой скорости:

$\begin{array}{l} v_{x} = 9,2 \cdot (0,5 + 1) \approx 14 м/с, \\ v_{y} = (- 4,6 \sqrt{3}) м/с . \end{array}}$

Модуль скорости лодки относительно берега рассчитаем по формуле

$v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{{(14)}^{2} + {(- 4,6 \sqrt{3})}^{2}} \approx 16$ м/с.