Физика

1.3.3. Некоторые дополнительные характеристики движения тела, брошенного под углом к горизонту вблизи поверхности Земли

Физика

1.3. Криволинейное движение тела

При криволинейном движении тела направление вектора скорости совпадает с направлением касательной, проведенной к той точке траектории движения тела, где оно находится в этот момент.

Величина скорости в произвольный момент времени

Модуль скорости тела v, брошенного под углом α к горизонту в поле силы тяжести Земли, в произвольный момент времени рассчитывается по теореме Пифагора:

$v = \sqrt{v_{x}^{2} + v_{y}^{2}}$ ,

где v_x и v_y — проекции скорости на соответствующие координатные оси:

1) для тела, брошенного с высоты h под углом α к горизонту (вверх) (см. рис. 1.27):

v_x = v₀ cos α = const,

v_y = v₀ sin α − gt;

2) для тела, брошенного с высоты h под углом α к горизонту (вниз) (см. рис. 1.28):

v_x = v₀ cos α = const,

v_y = −v₀ sin α − gt;

3) для тела, брошенного под углом α к горизонту с поверхности Земли (см. рис. 1.29):

v_x = v₀ cos α = const,

v_y = v₀ sin α − gt;

4) для тела, брошенного с высоты h горизонтально (см. рис. 1.30):

v_x = v₀ = const,

v_y = −gt,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

Угол между вектором скорости и линией горизонта

Угол β, который составляет вектор скорости с горизонтом в произвольный момент времени (рис. 1.31),

Рис. 1.31

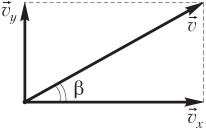
определяется формулой

$tg β = \frac{| v_{y} |}{v_{x}}$ ,

где v_x и v_y — проекции скорости на соответствующие координатные оси:

1) для тела, брошенного с высоты h под углом α к горизонту (вверх) (см. рис. 1.27):

v_x = v₀ cos α = const,

v_y = v₀ sin α − gt;

2) для тела, брошенного с высоты h под углом α к горизонту (вниз) (см. рис. 1.28):

v_x = v₀ cos α = const,

v_y = −v₀ sin α − gt;

3) для тела, брошенного под углом α к горизонту с поверхности Земли (см. рис. 1.29):

v_x = v₀ cos α = const,

v_y = v₀ sin α − gt;

4) для тела, брошенного с высоты h горизонтально (см. рис. 1.30):

v_x = v₀ = const,

v_y = −gt,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

Расстояние между телами, движущимися в поле силы тяжести

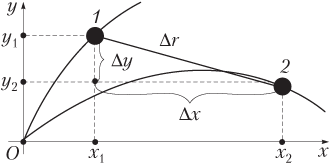
Если рассматривается движение двух тел (рис. 1.32), то расстояние между телами ∆r определяется c помощью выражения

$Δ r = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}} = \sqrt{{(Δ x)}^{2} + {(Δ y)}^{2}}$ ,

где x₁, y₁ — координаты положения первого тела в определенный момент времени; x₂, y₂ — координаты положения второго тела в этот же момент времени.

Рис. 1.32

Пример 20. Камень брошен с башни под углом 45° к горизонту со скоростью 15 м/с. Через какой интервал времени вектор скорости составит с горизонтом угол 30°?

Решение. Угол, который вектор скорости составит с горизонтом, определяется формулой

$tg β = \frac{| v_{y} |}{v_{x}}$ ,

где v_x и v_y — проекции вектора скорости на координатные оси; для данного случая указанные проекции определяются формулами

$v_{x} = v_{0} \cos α = 15 \cos 45 ° = 7,5 \sqrt{2}$ ,

$v_{y} = v_{0} \sin α - g t = 15 \sin 45 ° - 10 t = 7,5 \sqrt{2} - 10 t$ .

Подстановка v_x и v_y в исходную формулу дает уравнение

$tg β = tg 30 ° = \frac{| 7,5 \sqrt{2} - 10 t |}{7,5 \sqrt{2}} = \frac{1}{\sqrt{3}}$ , или $\frac{1}{\sqrt{3}} = \frac{| 7,5 \sqrt{2} - 10 t |}{7,5 \sqrt{2}}$ .

Данное уравнение содержит модуль разности двух величин $(7,5 \sqrt{2})$ и (10t); следовательно, оно эквивалентно двум независимым уравнениям:

$\frac{1}{\sqrt{3}} = 1 - \frac{10 t}{7,5 \sqrt{2}}$ и $\frac{1}{\sqrt{3}} = \frac{10 t}{7,5 \sqrt{2}} - 1$ .

Корень первого уравнения t₁ ≈ 0,45 c соответствует подъему тела; корень второго уравнения t₂ ≈ 1,67 c соответствует падению тела после его поднятия на максимальную высоту.

Пример 21. С башни высотой 40 м одновременно бросают два мяча: один — горизонтально со скоростью 10 м/с, другой — под углом 30° к горизонту (вниз) с той же скоростью. Найти расстояние между мячами спустя 1,0 с.

Решение. Уравнения движения первого мяча запишем в виде:

$\begin{array}{l} x_{1} (t) = v_{0} t = 10 t; \\ y_{1} (t) = h - \frac{g t^{2}}{2} = 40 - 5 t^{2} . \end{array}}$

Уравнения движения второго мяча —

$\begin{array}{l} x_{2} (t) = v_{0} t \cos α = 10 t \cos 30 ° = 5 t \sqrt{3}; \\ y_{2} (t) = h - v_{0} t \sin α - \frac{g t^{2}}{2} = 40 - 5 t - 5 t^{2} . \end{array}}$

Разность координат определяется формулами

$Δ x = | x_{2} - x_{1} | = 10 t (1 - 0,5 \sqrt{3})$ ;

$Δ y = | y_{2} - y_{1} | = 5 t$ .

Подстановка указанного в условии задачи значения времени t = 1,0 c в записанные уравнения позволяет вычислить значения ∆x и ∆y:

$Δ x = 10 \cdot 1,0 \cdot (1 - 0,5 \sqrt{3}) \approx 1,4$ м;

$Δ y = 5 \cdot 1,0 \approx 5,0$ м.

На рисунке показаны положения мячей в указанный момент времени.

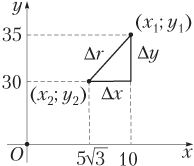
Расстояние между мячами вычислим по теореме Пифагора:

$Δ r = \sqrt{{(Δ x)}^{2} + {(Δ y)}^{2}} =$

$= \sqrt{{(1,4)}^{2} + {(5,0)}^{2}} \approx 5,2$ м.

Пример 24. Вычислить радиус кривизны траектории тела, брошенного под углом 30° к горизонту с начальной скоростью 10 м/с спустя 0,8 с после начала полета.

Решение. Радиус кривизны траектории определим по формуле

$R = \frac{v^{2}}{a_{n}}$ ,

где $v = \sqrt{v_{x}^{2} + v_{y}^{2}}$ — величина скорости тела в указанный момент времени; $v_{x} = v_{0} \cos 30^{°} = 5 \sqrt{3}$ м/с — проекция скорости на горизонтальную ось; $v_{y} = v_{0} \sin 30 ° - g t = - 3$ м/с — проекция скорости на вертикальную ось; $a_{n} = g \sin β$ — величина нормальной составляющей ускорения тела, $β = 90 ° - γ$ .

На рисунке показаны соответствующие углы, векторы скорости и ускорения тела.

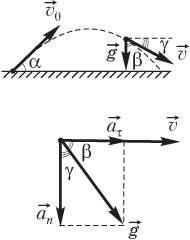
Тангенс угла γ можно определить с помощью формулы

$tg γ = \frac{| v_{y} |}{v_{x}} = \frac{| - 3 |}{5 \sqrt{3}} = 0,2 \sqrt{3} = 0,3464$ ,

что соответствует γ ≈ 20°.

Тогда угол $β = 90 ° - γ = 90 ° - 20 ° = 70 °$ , а величина нормального ускорения имеет значение:

$a_{n} = g \sin β = 10 \sin 70 ° \approx 10 \cdot 0,94 = 9,4$ м/с².

Модуль скорости тела рассчитаем, используя значения ее проекций для указанного момента времени:

$v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{{(5 \sqrt{3})}^{2} + {(- 3)}^{2}} \approx 9,2$ м/с.

Полученные значения скорости и нормального ускорения позволяют вычислить искомый радиус кривизны траектории:

$R = \frac{v^{2}}{a_{n}} = \frac{{(9,2)}^{2}}{9,4} \approx 9,0$ м.

Пример 25. Вычислить нормальное ускорение тела, брошенного под углом 60° к горизонту с поверхности Земли, в момент падения тела на Землю.

Решение. Если сопротивление воздуха отсутствует, то траекторией движения тела является симметричная парабола.

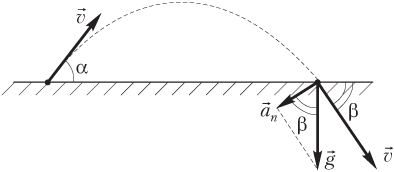
Углы α и β, показанные на рисунке, равны между собой:

α = β = 60°.

Величина нормального ускорения определяется формулой

$a_{n} = g \cos 60 ° = 10 \cdot 0,5 = 5,0$ м/с².