Предметы

Физика

Кинематика

1.3. Криволинейное движение тела

1.3.2. Движение тела, брошенного под углом к горизонту вблизи поверхности Земли

Теория Тренинг

Физика

Общий тест

1.3. Криволинейное движение тела

1.3.2. Движение тела, брошенного под углом к горизонту вблизи поверхности Земли

Движение тела, брошенного под углом к горизонту вблизи поверхности Земли, представляет собой комбинацию двух видов движения: равномерного вдоль оси Ox и равнопеременного вдоль оси Oy.

Уравнения движения и закон изменения проекций скорости с течением времени

Уравнения движения тела, брошенного под углом к горизонту вблизи поверхности Земли, в координатной форме имеют вид:

$\begin{array}{l} x (t) = v_{0 x} t, \\ y (t) = y_{0} + v_{0 y} t + \frac{a_{y} t^{2}}{2} . \end{array}}$

Значения y₀ (начальной координаты), v₀_x и v₀_y (проекции начальной скорости на координатные оси) различаются для разных ситуаций; значение a_y (проекция ускорения на ось Oy) всегда одинаково:

a_y = −g,

где g = 10 м/с².

Проекция скорости тела, брошенного под углом к горизонту вблизи поверхности Земли, на ось Ox остается постоянной величиной:

v_x = v₀_x = const,

а на ось Oy — меняется по закону

v_y = v₀_y − gt,

где v₀_x, v₀_y — проекции начальной скорости на координатные оси; g — ускорение свободного падения; t — время движения.

В процессе движения тела, брошенного под углом α с поверхности Земли (рис. 1.26):

его скорость принимает максимальные значения в точке бросания (v₁) и в точке падения тела на Землю (v₂), равные начальной скорости (v₀):
$v_{max} = v_{1} = v_{2} = v_{0}$
в наивысшей точке подъема тело имеет минимальную скорость v₃:
$v_{min} = v_{3} = v_{0} \cos α$ .

Рис. 1.26

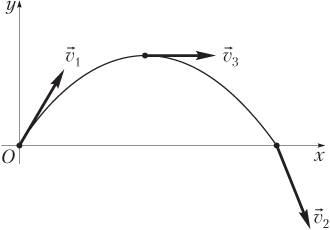
В наивысшей точке подъема скорость тела направлена горизонтально.

Для тела, брошенного с высоты h под углом α к горизонту (вверх) (рис. 1.27), зависимости x- и y-координат от времени (уравнения движения) имеют вид:

$x (t) = v_{0} t \cos α$ , $y (t) = h + v_{0} t \sin α - \frac{g t^{2}}{2}$ ,

Рис. 1.27

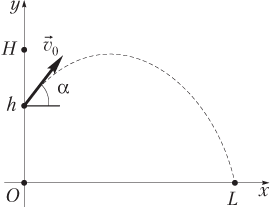
а проекции скорости на соответствующие координатные оси изменяются по законам

v_x = v₀ cos α = const,

v_y = v₀ sin α − gt,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

Для тела, брошенного с высоты h под углом α к горизонту (вниз) (рис. 1.28), зависимости x- и y-координат от времени (уравнения движения) имеют вид:

$x (t) = v_{0} t \cos α$ ,

$y (t) = h - v_{0} t \sin α - \frac{g t^{2}}{2}$ ,

Рис. 1.28

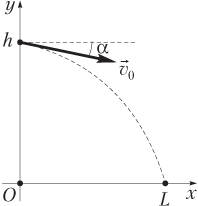
а проекции скорости на соответствующие координатные оси изменяются по законам

v_x = v₀ cos α = const,

v_y = −v₀ sin α − gt,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

Для тела, брошенного под углом α к горизонту с поверхности Земли (рис. 1.29), зависимости x- и y-координат от времени (уравнения движения) имеют вид:

$x (t) = v_{0} t \cos α$ ,

$y (t) = v_{0} t \sin α - \frac{g t^{2}}{2}$ ,

Рис. 1.29

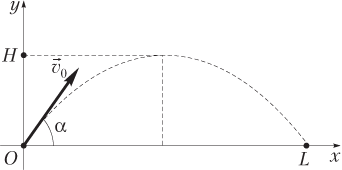
а проекции скорости на соответствующие координатные оси изменяются по законам

v_x = v₀ cos α = const,

v_y = v₀ sin α − gt,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

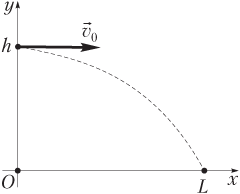
Для тела, брошенного с высоты h горизонтально (рис. 1.30), зависимости x- и y-координат от времени (уравнения движения) имеют вид:

x(t) = v₀t,

$y (t) = h - \frac{g t^{2}}{2}$ ,

Рис. 1.30

а проекции скорости на соответствующие координатные оси изменяются по законам

v_x = v₀ = const,

v_y = −gt,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

Время полета

В момент времени, соответствующий времени полета t = t_пол, y-координата обращается в ноль:

y(t_пол) = 0.

Это уравнение позволяет найти время полета тела. Зависимости y-координаты от времени выбираются в соответствии с характером движения тела:

1) для тела, брошенного с высоты h под углом α к горизонту (вверх) (см. рис. 1.27):

$h + v_{0} t_{пол} \sin α - \frac{g t_{пол}^{2}}{2} = 0$ ;

2) для тела, брошенного с высоты h под углом α к горизонту (вниз) (см. рис. 1.28):

$h - v_{0} t_{пол} \sin α - \frac{g t_{пол}^{2}}{2} = 0$ ;

3) для тела, брошенного под углом α к горизонту с поверхности Земли (см. рис. 1.29):

$v_{0} t_{пол} \sin α - \frac{g t_{пол}^{2}}{2} = 0$ ;

4) для тела, брошенного с высоты h горизонтально (см. рис. 1.30):

$h - \frac{g t_{пол}^{2}}{2} = 0$ ,

где v₀ — начальная скорость движения; g — ускорение свободного падения.

Дальность полета

В момент времени, соответствующий времени полета t = t_пол, x-координата принимает максимальное значение, соответствующее дальности полета L:

L = x(t_пол).

Зависимости x-координаты от времени выбираются в соответствии с характером движения тела:

1) для тела, брошенного с высоты h под углом α к горизонту (вверх) (см. рис. 1.27):

L = v₀t_пол cos α;

2) для тела, брошенного с высоты h под углом α к горизонту (вниз) (см. рис. 1.28):

L = v₀t_пол cos α;

3) для тела, брошенного под углом α к горизонту с поверхности Земли (см. рис. 1.29):

L = v₀t_пол cos α;

4) для тела, брошенного с высоты h горизонтально (см. рис. 1.30):

L = v₀t_пол,

где v₀ — начальная скорость движения.

Время подъема до максимальной высоты

Проекция скорости тела на ось Oy при движении вверх уменьшается. В момент времени t = t_под, соответствующий времени подъема y-проекция скорости тела обращается в нуль:

v_y(t_под) = 0.

Это уравнение позволяет найти время подъема тела до максимальной высоты. Зависимости y-проекции скорости от времени выбираются в соответствии с характером движения тела:

1) для тела, брошенного с высоты h под углом α к горизонту (вверх) (см. рис. 1.27):

v₀ sin α − gt_под = 0;

2) для тела, брошенного под углом α к горизонту с поверхности Земли (см. рис. 1.29):

v₀ sin α − gt_под = 0,

где v₀ — начальная скорость движения; g — ускорение свободного падения.

Следует отметить, что для случаев движения тела, брошенного с высоты h под углом α к горизонту (вниз), и для тела, брошенного с высоты h горизонтально, указанная характеристика движения отсутствует.

Максимальная высота подъема

В момент времени, соответствующий времени подъема t = t_под, y-координата принимает максимальное значение, соответствующее максимальной высоте подъема H:

H = y(t_под).

Зависимости y-координаты от времени выбираются в соответствии с характером движения тела:

1) для тела, брошенного с высоты h под углом α к горизонту (вверх) (см. рис. 1.27):

$H = h + v_{0} t_{под} \sin α - \frac{g t_{под}^{2}}{2}$ ;

2) для тела, брошенного под углом α к горизонту с поверхности Земли (см. рис. 1.29):

$H = v_{0} t_{под} \sin α - \frac{g t_{под}^{2}}{2}$ ,

где v₀ — начальная скорость; t — время движения; g — ускорение свободного падения.

Пример 22. Во сколько раз отличаются дальности полета двух тел, одно из которых брошено с башни высотой 20 м со скоростью 15 м/с горизонтально, а второе — с поверхности Земли от основания башни под углом 60° к горизонту с той же скоростью?

Решение. Уравнения движения первого тела запишем в виде:

$\begin{array}{l} x_{1} (t) = v_{0} t = 15 t; \\ y_{1} (t) = h - \frac{g t^{2}}{2} = 20 - 5 t^{2} . \end{array}}$

Вычислим время полета первого тела τ₁ из условия y₁(τ₁) = 0, или в явном виде:

$20 - 5 τ_{1}^{2} = 0$ .

Решение данного уравнения дает время полета первого тела τ₁ = 2,0 с.

Рассчитаем дальность полета первого тела, подставив найденное значение τ₁ = 2,0 с в уравнение L₁ = x₁(τ₁):

$L_{1} = x_{1} (τ_{1}) = 15 τ_{1} = 15 \cdot 2,0 = 30$ м.

Уравнения движения второго тела запишем в виде:

$\begin{array}{l} x_{2} (t) = v_{0} t \cos α = 15 t \cos 60 ° = 7,5 t; \\ y_{2} (t) = v_{0} t \sin α - \frac{g t^{2}}{2} = 15 t \sin 60 ° - 5 t^{2} = 7,5 t \sqrt{3} - 5 t^{2} . \end{array}}$

Вычислим время полета второго тела τ₂ из условия y₂(τ₂) = 0, или в явном виде:

$7,5 τ_{2} \sqrt{3} - 5 τ_{2}^{2} = 0$ .

Решение данного уравнения дает время полета второго тела $τ_{2} = 1,5 \sqrt{3}$ с.

Рассчитаем дальность полета второго тела, подставив найденное значение $τ_{2} = 1,5 \sqrt{3}$ с в уравнение $L_{2} = x_{2} (τ_{2})$ :

$L_{2} = x_{2} (τ_{2}) = 7,5 τ_{2} = 7,5 \cdot 1,5 \sqrt{3} = 11,25 \sqrt{3}$ м.

Искомое отношение дальностей полета первого и второго тел:

$\frac{L_{1}}{L_{2}} = \frac{30}{11,25 \sqrt{3}} \approx 1,5$ .

Таким образом, дальность полета первого тела приблизительно в 1,5 раза превышает дальность полета второго тела.

Пример 23. Во сколько раз время полета тела, брошенного с башни высотой 18 м под углом 30° к горизонту вверх, больше времени полета тела, брошенного с той же башни с такой же начальной скоростью, но под углом 30° к горизонту вниз? Начальную скорость принять равной 30 м/с.

Решение. Уравнения движения первого тела запишем в виде:

$\begin{array}{l} x_{1} (t) = v_{0} t \cos α = 30 t \cos 30 ° = 15 t \sqrt{3}; \\ y_{1} (t) = h + v_{0} t \sin α - \frac{g t^{2}}{2} = 18 + 30 t \sin 30 ° - 5 t^{2} = 18 + 15 t - 5 t^{2} . \end{array}}$

Вычислим время полета первого тела τ₁ из условия y₁(τ₁) = 0, или в явном виде:

$18 + 15 τ_{1} - 5 τ_{1}^{2} = 0$ .

Физический смысл имеет корень данного уравнения τ₁ = 3,9 с.

Уравнения движения второго тела запишем в виде:

$\begin{array}{l} x_{2} (t) = v_{0} t \cos α = 30 t \cos 30 ° = 15 t \sqrt{3} \\ y_{2} (t) = h - v_{0} t \sin α - \frac{g t^{2}}{2} = 18 - 30 t \sin 30 ° - 5 t^{2} = 18 - 15 t - 5 t^{2} . \end{array}}$

Вычислим время полета второго тела τ₂ из условия y₂(τ₂) = 0, или в явном виде:

$18 - 15 τ_{2} - 5 τ_{2}^{2} = 0$ .

Физический смысл имеет корень данного уравнения τ₂ = 0,9 с.

Искомое отношение времени полета первого тела ко времени полета второго тела:

$\frac{τ_{1}}{τ_{2}} = \frac{3,9}{0,9} \approx 4,3$ .

Таким образом, время полета первого тела приблизительно в 4,3 раза превышает время полета второго тела.