Предметы

Физика

Кинематика

1.3. Криволинейное движение тела

1.3.1. Движение тела по окружности

Теория Тренинг

Физика

Общий тест

1.3. Криволинейное движение тела

1.3.1. Движение тела по окружности

Угловые характеристики движения

При рассмотрении движения материальной точки (тела) по окружности пользуются не только линейными характеристиками (перемещение, скорость и ускорение), но и угловыми (угловое перемещение, угловая скорость, угловое ускорение).

Угловая скорость $\vec{ω}$ — это векторная физическая величина, характеризующая быстроту углового перемещения, численно равная отношению угла поворота ∆φ ко времени ∆t, за которое этот поворот произошел:

$ω = \frac{Δ φ}{Δ t}$ .

Направление $\vec{ω}$ определяется правилом правого винта.

Данное определение является корректным только для случая равномерного движения материальной точки по окружности. При неравномерном движении по окружности пользуются понятиями мгновенной угловой скорости и углового ускорения.

Угловое ускорение $\vec{β}$ — это векторная физическая величина, характеризующая быстроту изменения угловой скорости, численно равная отношению изменения угловой скорости ∆ω к тому интервалу времени ∆t, за которой это изменение произошло:

$β = \frac{Δ ω}{Δ t}$ .

Направление $\vec{β}$ совпадает с направлением $\vec{ω}$ , если угловая скорость увеличивается, и противоположно $\vec{ω}$ , если угловая скорость уменьшается. Данное определение правомерно только для равнопеременного движения материальной точки по окружности.

В Международной системе единиц угловое перемещение (угол поворота) измеряется в радианах (1 рад), угловая скорость — в радианах в секунду (1 рад/с), угловое ускорение — в радианах в секунду за секунду (1 рад/с²).

Связь угловых характеристик движения с линейными

Угловые и линейные характеристики движения связаны между собой.

При равномерном движении по окружности

координаты положения материальной точки в определенный момент времени x(t) и y(t) могут быть выражены через ее угловое положение в этот момент времени φ(t) формулами (рис. 1.25):
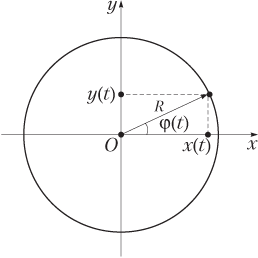
$\begin{matrix} x (t) = R \cos φ (t), \\ y (t) = R \sin φ (t); \end{matrix}}$

Рис. 1.25

модуль линейной скорости v может быть выражен через величину угловой скорости ω: v = ωR;
величина углового ускорения точки равна нулю: β = 0.

Специальные характеристики движения

При рассмотрении равномерного движения точки по окружности также вводятся специальные характеристики движения: период, частота, циклическая частота, центростремительное ускорение.

Период — время одного оборота — определяется с помощью выражения

$T = \frac{t}{n}$ ,

где n — число оборотов материальной точки за время t. В Международной системе единиц период измеряется в секундах (1 с).

Частота — количество оборотов в единицу времени:

$ν = \frac{1}{T}$ .

В Международной системе единиц частота измеряется в секундах в минус первой степени, или герцах (1 с⁻¹ = 1 Гц).

Циклическая частота численно совпадает с угловой скоростью материальной точки и определяется как

ω = 2πν.

В Международной системе единиц циклическая частота измеряется в радианах в секунду (1 рад/с).

Центростремительное ускорение определяется одной из трех формул:

$a_{ц . с} = \frac{v^{2}}{R}$ , a_ц.с = ω²R, a_ц.с = ωv.

В Международной системе единиц центростремительное ускорение измеряется в метрах в секунду за секунду (1 м/с².)

Уравнения движения и зависимость угловой скорости от времени

При равномерном движении точки по окружности угловая скорость постоянна:

ω = const;

угловое положение материальной точки φ в произвольный момент времени t описывается уравнением, аналогичным уравнению равномерного прямолинейного движения (x(t) = x₀ + vt):

φ(t) = φ₀ + ωt,

где φ₀ — угловое положение точки в начальный момент времени; ω — величина угловой скорости материальной точки.

При равноускоренном движении материальной точки по окружности уравнение движения (зависимость углового положения точки от времени φ(t)) и закон изменения угловой скорости с течением времени ω(t) по форме совпадают с соответствующими уравнениями для равноускоренного прямолинейного движения:

$φ (t) = φ_{0} + ω_{0} t + \frac{β t^{2}}{2}$ , ω(t) = ω₀ + βt,

где φ₀ — угловое положение материальной точки в начальный момент времени; ω₀ — величина начальной угловой скорости; β — модуль углового ускорения.

При равнозамедленном движении материальной точки по окружности уравнение движения φ(t) и закон изменения скорости ω(t) записываются по аналогии с соответствующими уравнениями для равнозамедленного прямолинейного движения:

$φ (t) = φ_{0} + ω_{0} t - \frac{β t^{2}}{2}$ , ω(t) = ω₀ − βt,

Пример 14. Небольшое тело начинает движение по окружности радиусом 80 м с постоянным по модулю тангенциальным ускорением 4,0 м/с². Найти полное ускорение тела спустя 8,0 с после начала движения.

Решение. Движение тела является равнопеременным движением по окружности. Вычисление модуля полного ускорения произведем по формуле

$| \vec{a} | = \sqrt{a_{τ}^{2} + a_{n}^{2}}$ ,

где a_τ = 4,0 м/с² — величина тангенциального ускорения тела (постоянная величина).

Величину нормального ускорения a_n определим по формуле

$a_{n} (t) = \frac{v^{2} (t)}{R}$ ,

где R = 80 м — радиус окружности; v(t) = a_τt = 4,0t — зависимость величины линейной скорости тела от времени при равнопеременном движении по окружности без начальной скорости.

Для вычисления модуля полного ускорения подставим в исходную формулу выражения, определяющие a_τ и a_n(t),

$| \vec{a} | = \sqrt{a_{τ}^{2} + {(\frac{v^{2} (t)}{R})}^{2}} = \sqrt{{(4,0)}^{2} + {(\frac{{(4,0 t)}^{2}}{R})}^{2}}$ .

Произведем расчет:

$| \vec{a} | = 4,0 \sqrt{1 + \frac{{(4,0)}^{2} \cdot {(8,0)}^{4}}{80^{2}}} \approx 13$ м/с².

Пример 15. Диск радиусом 1,0 м равномерно вращается относительно оси, проходящей через его центр перпендикулярно поверхности. На каком расстоянии друг от друга могут находиться точки диска, если отношение их линейных скоростей равно $\sqrt{2}$ ?

Решение. При равномерном вращении диска угловая скорость остается постоянной для всех его точек:

ω = const.

Значения линейных скоростей двух точек диска, находящихся на расстояниях l₁ и l₂ от его центра, определяются по формулам

v₁ = ωl₁ и v₂ = ωl₂,

где v₁ — величина линейной скорости точки A, расположенной на расстоянии l₁ от центра диска; v₂ — величина линейной скорости точки B, расположенной на расстоянии l₂ от центра диска.

Отношение линейных скоростей точек A и B по условию задачи составляет:

$\frac{v_{1}}{v_{2}} = \frac{l_{1}}{l_{2}} = \sqrt{2}$ .

Предположим, что одна из точек (точка A) находится на расстоянии радиуса от центра диска (l₁ = R).

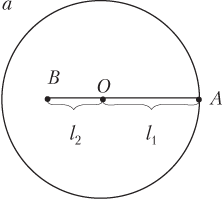
Возможны два предельных варианта положения точек A и B, которые показаны на рис. а, б.

1) в первом случае (рис. а) расстояние между точками является максимальным:

r_max = l₁ + l₂,

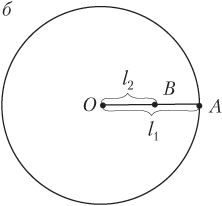
2) во втором случае (рис. б) расстояние между точками является минимальным:

r_min = l₁ − l₂,

где l₁ = R; $l_{2} = R / \sqrt{2}$ .

Подстановка выражений для l₁ и l₂ в соответствующие формулы позволяет вычислить указанные расстояния:

$r_{max} = l_{1} + l_{2} = R + \frac{R}{\sqrt{2}} = R (1 + \frac{1}{\sqrt{2}}) = R (1 + 0,5 \sqrt{2}) \approx 1,7$ м;

$r_{min} = l_{1} - l_{2} = R - \frac{R}{\sqrt{2}} = R (1 - \frac{1}{\sqrt{2}}) = R (1 - 0,5 \sqrt{2}) \approx 0,3$ м.

Точки диска с заданным в условии соотношением линейных скоростей могут находиться на расстояниях от 0,3 м до 1,7 м друг от друга.

Пример 16. Угол поворота колеса радиусом 0,1 м изменяется с течением времени по закону φ = πt, где угол задан в радианах, время — в секундах. Найти угловую и линейную скорости, а также центростремительное ускорение точек обода колеса.

Решение. При равномерном движении точки по окружности ее угловое положение задается уравнением

φ = φ₀ + ωt,

где φ₀ — угловое положение точки в начальный момент времени; ω — модуль угловой скорости.

Приведенный в условии задачи угол поворота представляет собой угловое перемещение точки обода колеса и определяется формулой

∆φ = φ(t) − φ(0) = ωt,

где φ(0) = φ₀ — угловое положение точки обода колеса в начальный момент времени; φ(t) = φ₀ + ωt — угловое положение точки обода колеса в момент времени t; ω = π рад/с — модуль угловой скорости.

Таким образом, величина угловой скорости точки обода колеса составляет

ω = 3,14 рад/с.

Линейная скорость точки обода колеса определяется формулой

v = ωR

и имеет значение:

v = π ⋅ 0,1 ≈ 0,314 м/с = 31,4 см/с.

Центростремительное ускорение точки обода колеса вычислим по формуле

$a_{ц . с} = a_{n} = ω^{2} R$ ;

вычисление дает значение

$a_{ц . с} = π^{2} \cdot 0,1 \approx 1,0$ м/с².

Пример 17. Найти линейную скорость и центростремительное ускорение точек земной поверхности на экваторе и на широте 45°. Радиус Земли считать равным 6,4 ⋅ 10⁶ м.

Решение. 1) Точка экватора движется по окружности радиусом R и совершает один оборот за время, равное периоду обращения Земли вокруг своей оси (сутки):

$T = \frac{2 π R}{v_{1}}$ ,

где R = 6,4 ⋅ 10⁶ м — радиус Земли; v₁ — модуль линейной скорости точки (искомая величина). Рисунок иллюстрирует данную ситуацию.

Из приведенной формулы следует, что модуль линейной скорости точки

$v_{1} = \frac{2 π R}{T} = \frac{2 π \cdot 6,4 \cdot 10^{6}}{24 \cdot 3600} = 465$ м/с.

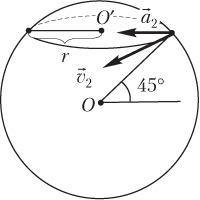
2) Точка, находящаяся на широте 45°, движется по окружности радиусом r и совершает один оборот за время равное, как и в предыдущем случае, периоду обращения Земли вокруг своей оси (сутки):

$T = \frac{2 π r}{v_{2}}$ ,

где r = R cos 45° — радиус окружности для точки, находящейся на указанной широте; R — радиус Земли; v₂ — модуль линейной скорости точки, находящейся на указанной широте (искомая величина). Рисунок иллюстрирует данную ситуацию.

Из приведенной формулы следует, что модуль линейной скорости точки

$v_{2} = \frac{2 π r}{T} = \frac{2 π R \cos 45 °}{T_{2}} = \frac{2 π \cdot 6,4 \cdot 10^{6} \cdot 0,5 \sqrt{2}}{24 \cdot 3600} = 328$ м/с.

3) Центростремительное ускорение точки, находящейся на экваторе, определяется квадратом ее линейной скорости v₁ и радиусом окружности R, по которой она движется:

$a_{ц . с 1} = \frac{v_{1}^{2}}{R}$ .

Центростремительное ускорение точки, находящейся на широте 45°, определяется квадратом ее линейной скорости v₂ и радиусом окружности $r = R \cos 45 °$ , по которой она движется:

$a_{ц . с 2} = \frac{v_{2}^{2}}{r} = \frac{v_{2}^{2}}{R \cos 45 °}$ .

Для вычисления модулей центростремительных ускорений воспользуемся полученными выше значениями линейных скоростей:

$a_{ц . с 1} = \frac{{(465)}^{2}}{6,4 \cdot 10^{6}} \approx 3,4 \cdot 10^{- 2} {м/с}^{2} = 3,4 {см/с}^{2}$ ;

$a_{ц . с 2} = \frac{{(328)}^{2}}{6,4 \cdot 10^{6} \cdot 0,5 \sqrt{2}} \approx 2,4 \cdot 10^{- 2} {м/с}^{2} = 2,4 {см/с}^{2}$ .

Пример 18. К валу, радиус которого равен 10 см, прикреплена нить. Через 5,0 с от начала равномерного вращения вала на него намоталось 4,0 м нити. Определить частоту вращения вала.

Решение. Частота вращения вала определяется выражением

$ν = \frac{1}{T}$ ,

где T — период (время одного оборота), определяемый по формуле

$T = \frac{t}{n}$ ,

где n — число оборотов вала; t — время, за которое происходит n оборотов.

По условию задачи указанное время составляет t = 5,0 с, а число оборотов вала определим как отношение длины намотанной на вал нити L = 4,0 м к длине окружности вала l = 2πR, т.е.

$n = \frac{L}{l} = \frac{L}{2 π R}$ ,

где R = 0,10 м — радиус вала.

Для расчета искомой частоты получим следующую формулу:

$ν = \frac{1}{T} = \frac{n}{t} = \frac{L}{l t} = \frac{L}{2 π R t}$ .

Произведем вычисление:

$ν = \frac{4,0}{2 π \cdot 0,10 \cdot 5,0} \approx 1,3$ Гц.

Пример 19. На вал радиусом 10 см намотана нить, к концу которой привязана гиря. Двигаясь равноускоренно, гиря за 20 с от начала движения опустилась на 2,0 м. Найти модуль углового ускорения и модуль угловой скорости вала в этот момент времени.

Решение. Гиря опускается вертикально вниз; ее движение вдоль координатной оси, направление которой совпадает с направлением движения гири, происходит по закону

$y (t) = \frac{a t^{2}}{2}$ ,

где a — модуль ускорения гири; t — время.

Зависимость модуля скорости гири от времени при ее равноускоренном движении задается выражением

v(t) = at.

За интервал времени ∆t = τ вертикальная координата гири изменяется на величину

$Δ y = H = \frac{a τ^{2}}{2}$ .

Следовательно, модуль ускорения гири определяется формулой

$a = \frac{2 H}{τ^{2}}$ ,

а величина ее скорости составляет

$v (τ) = a τ = \frac{2 H}{τ^{2}} τ = \frac{2 H}{τ} = \frac{2 \cdot 2,0}{20} = 0,2 м/с = 20 см/с$ .

Считая, что величина линейной скорости точек вала совпадает с величиной скорости гири, определим угловую скорость вала для указанного в условии момента времени:

$ω (τ) = \frac{v (τ)}{R} = \frac{0,2}{0,1} = 2,0$ рад/с.

Для нахождения углового ускорения установим зависимость угловой скорости вала от времени ω(t), подставив зависимость v(t) в формулу связи угловой и линейной скорости:

$ω (t) = \frac{v (t)}{R} = \frac{a t}{R}$ ,

где $a = \frac{2 H}{τ^{2}}$ , т.е.

$ω (t) = \frac{2 H t}{R τ^{2}}$ .

Сравнение этого выражения с $ω (t) = β t$ дает формулу для вычисления модуля углового ускорения β:

$β = \frac{2 H}{R τ^{2}} = \frac{2 \cdot 2,0}{0,10 \cdot 20^{2}} = 0,10$ рад/с².