Физика

Криволинейным движением называют движение, при котором направление скорости материальной точки (тела) изменяется с течением времени. При этом

• модуль (величина) скорости может оставаться постоянным — равномерное криволинейное движение;
• или меняться со временем — неравномерное криволинейное движение.

Примером равномерного криволинейного движения служит равномерное движение по окружности, примером неравномерного криволинейного движения — движение тела, брошенного под углом к горизонту в поле силы тяжести.

Траекторией движения при криволинейном движении является кривая линия.

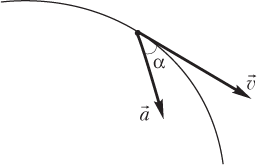
При криволинейном движении вектор скорости и вектор ускорения образуют между собой угол α (рис. 1.23).

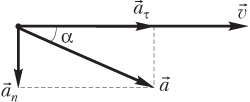
Вектор ускорения может быть разложен на две составляющие (рис. 1.24):

$\overrightarrow{a}={\overrightarrow{a}}_{\tau }+{\overrightarrow{a}}_n$,

где ${\overrightarrow{a}}_{\tau }$ — тангенциальная составляющая, направленная вдоль вектора скорости и отвечающая за изменение модуля скорости с течением времени:

$\left|{\overrightarrow{a}}_{\tau }\right|=\left|v^{\prime }\left(t\right)\right|$,

где v′(t) — производная скорости по времени; ${\overrightarrow{a}}_n$ — нормальная составляющая ускорения, направленная перпендикулярно вектору скорости и отвечающая за изменение направления вектора скорости с течением времени:

$\left|{\overrightarrow{a}}_n\right|=\frac{v^2}{R\left(t\right)}$,

где R(t) — радиус кривизны траектории тела в определенный момент времени t.

Модуль ускорения $\overrightarrow{a}$ в этом случае вычисляется с помощью теоремы Пифагора, так как его тангенциальная ${\overrightarrow{a}}_{\tau }$ и нормальная ${\overrightarrow{a}}_n$ составляющие взаимно перпендикулярны:

$\left|\overrightarrow{a}\right|=\sqrt{{\left|{\overrightarrow{a}}_{\tau }\right|}^2+{\left|{\overrightarrow{a}}_n\right|}^2}$.

При равномерном движении материальной точки (тела) по окружности величина тангенциальной составляющей ускорения обращается в ноль, так как модуль скорости остается неизменным:

$\left|{\overrightarrow{a}}_{\tau }\right|=0$,

$\left|{\overrightarrow{a}}_n\right|=\frac{v^2}{R}$,

где R — радиус окружности; в этом случае нормальное ускорение называется центростремительным, так как оно всегда направлено к центру окружности.