Предметы

Физика

Кинематика

1.2. Прямолинейное движение

1.2.5. Вертикальное движение тела вблизи поверхности Земли

Теория Тренинг

Физика

Общий тест

1.2. Прямолинейное движение

1.2.5. Вертикальное движение тела вблизи поверхности Земли

Вертикальное движение тела вблизи поверхности Земли является частным случаем равнопеременного прямолинейного движения. При решении задач о движении тела вблизи поверхности Земли следует считать, что сопротивление воздуха отсутствует.

При вертикальном движении вблизи поверхности Земли в отсутствие сопротивления воздуха ускорение тела $\vec{a}$ совпадает с ускорением свободного падения $\vec{g}$ , которое при решении задач принято считать равным: a = g ≈ 10 м/с².

Уравнение движения и зависимость проекции скорости от времени

Для тела, свободно падающего с высоты h (рис. 1.19), зависимость координаты y от времени t имеет вид:

$y = h - \frac{g t^{2}}{2}$ ,

Рис. 1.19

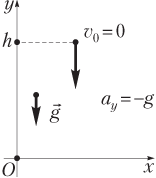
а проекция скорости на ось Oy изменяется по закону

v_y = −gt,

где g = 10 м/с².

Для тела, брошенного с высоты h вниз с начальной скоростью ${\vec{v}}_{0}$ (рис. 1.20), зависимость координаты y от времени t имеет вид:

$y = h - v_{0} t - \frac{g t^{2}}{2}$ ,

Рис. 1.20

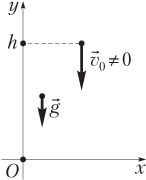
а проекция скорости на ось Oy изменяется по закону

v_y = −v₀ − gt,

где g = 10 м/с².

Для тела, брошенного с высоты h вверх с начальной скоростью ${\vec{v}}_{0}$ (рис. 1.21), зависимость координаты y от времени t имеет вид:

$y = h + v_{0} t - \frac{g t^{2}}{2}$ ,

Рис. 1.21

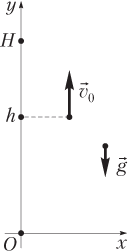
а проекция скорости на ось Oy изменяется по закону

v_y = v₀ − gt,

где g = 10 м/с².

Для тела, брошенного с поверхности Земли вверх с начальной скоростью ${\vec{v}}_{0}$ (рис. 1.22), зависимость координаты y от времени t имеет вид:

$y = v_{0} t - \frac{g t^{2}}{2}$ ,

Рис. 1.22

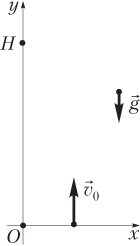
а проекция скорости на ось Oy изменяется по закону

v_y = v₀ − gt,

где g = 10 м/с².

Время полета

В момент времени, соответствующий времени полета t = t_пол, координата y обращается в ноль:

y(t_пол) = 0.

Это уравнение позволяет найти время полета тела.

Зависимости координаты y от времени выбираются в соответствии с характером движения тела:

1) для тела, свободно падающего с высоты h (см. рис. 1.19):

$h - \frac{g t_{пол}^{2}}{2} = 0$ ;

2) для тела, брошенного с высоты h вниз с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.20):

$h - v_{0} t_{пол} - \frac{g t_{пол}^{2}}{2} = 0$ ;

3) для тела, брошенного с высоты h вверх с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.21):

$h + v_{0} t_{пол} - \frac{g t_{пол}^{2}}{2} = 0$ ;

4) для тела, брошенного с поверхности Земли вверх с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.22):

$v_{0} t_{пол} - \frac{g t_{пол}^{2}}{2} = 0$ .

Время подъема до максимальной высоты

Модуль скорости тела при движении вверх уменьшается по закону

v(t) = |v₀ − gt|.

В момент времени t, соответствующий времени подъема тела t_под, скорость тела обращается в ноль; отсюда находим:

$t = t_{под} = \frac{v_{0}}{g}$ ,

где g = 10 м/с².

Это уравнение позволяет найти время подъема тела до максимальной высоты. Зависимости y-проекции скорости от времени выбираются в соответствии с характером движения тела:

1) для тела, брошенного с высоты h вверх с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.21):

$v_{0} - g t_{под} = 0$ ;

2) для тела, брошенного с поверхности Земли вверх с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.22):

$v_{0} - g t_{под} = 0$ .

Следует отметить, что для случаев движения тела, свободно падающего с определенной высоты, и тела, брошенного вниз, указанная характеристика движения отсутствует.

Максимальная высота подъема

В момент времени, соответствующий времени подъема t = t_под, координата y принимает максимальное значение, соответствующее максимальной высоте подъема H:

H = y(t_под).

Зависимости координаты y от времени выбираются в соответствии с характером движения тела:

1) для тела, брошенного с высоты h вверх с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.21):

$H = h + v_{0} t_{под} - \frac{g t_{под}^{2}}{2}$ ;

2) для тела, брошенного с поверхности Земли вверх с начальной скоростью ${\vec{v}}_{0}$ (см. рис. 1.22):

$H = v_{0} t_{под} - \frac{g t_{под}^{2}}{2}$ .

Пример 11. Тело, брошенное с поверхности Земли вертикально вверх со скоростью 30 м/с, побывало на высоте 30 м дважды. Найти интервал времени, разделяющий эти события.

Решение. Движение тела, брошенного вертикально вверх с поверхности Земли, описывается уравнением

$y (t) = v_{0} t - \frac{g t^{2}}{2}$ ,

где v₀ = 30 м/с — модуль начальной скорости тела; g = 10 м/с² — модуль ускорения свободного падения.

Подстановка в уравнение движения тела значений начальной скорости и ускорения свободного падения позволяет записать его в виде:

y(t) = 30t − 5,0t².

При y(t) = 30 м имеем

30 = 30t − 5,0t²,

или

t² − 6t + 6 = 0.

Корни уравнения

$t_{1} = (3,0 - \sqrt{3})$ с и $t_{2} = (3,0 + \sqrt{3})$ с

соответствуют моментам времени, когда тело оказывается на указанной в условии высоте.

Искомый интервал времени определяется разностью

$Δ t = t_{2} - t_{1} = (3,0 + \sqrt{3}) - (3,0 - \sqrt{3}) = 2,0 \sqrt{3} \approx 3,5$ с.

Пример 12. Тело брошено вертикально вверх с высоты 25 м с начальной скоростью 10 м/с. Какую часть времени полета тело двигалось равнозамедленно?

Решение. Движение тела является равнозамедленным до тех пор, пока оно не достигнет максимальной высоты подъема H. Время подъема до максимальной высоты определяется формулой

$t_{под} = \frac{v_{0}}{g}$ ,

где v₀ = 10 м/с — модуль начальной скорости тела; g = 10 м/с² — модуль ускорения свободного падения.

Подстановка в записанную формулу значений начальной скорости и ускорения свободного падения позволяет вычислить время подъема:

$t_{под} = \frac{10}{10} = 1,0$ c.

Для определения времени полета тела запишем уравнение движения тела. Движение тела, брошенного вертикально вверх с определенной высоты, описывается уравнением

$y (t) = h + v_{0} t - \frac{g t^{2}}{2}$ .

Подстановка значений v₀ = 10 м/с, g = 10 м/с² и h = 25 м позволяет записать уравнение движения в явном виде:

$y (t) = 25 + 10 t - 5,0 t^{2}$ .

Время полета тела определим из условия y(t_пол) = 0, т.е.

$25 + 10 t_{пол} - 5,0 t_{пол}^{2} = 0$ , или $t_{пол}^{2} - 2,0 t_{пол} - 5,0 = 0$ .

Корнями этого уравнения являются $t_{1} = (1,0 - \sqrt{6})$ и $t_{2} = (1,0 + \sqrt{6})$ с, первый из которых не имеет физического смысла. Таким образом, время полета тела равно

$t_{пол} = (1,0 + \sqrt{6})$ с.

Доля равнозамедленного движения тела определяется отношением времени подъема тела ко времени его полета:

$η = \frac{t_{под}}{t_{пол}} = \frac{1,0}{1,0 + \sqrt{6}} \approx 0,3$ .

Пример 13. Тело проходит последнюю треть пути за 0,5 с. Считая движение тела свободным падением, определить высоту, с которой падало тело.

Решение. Запишем уравнение движения тела в виде

$y (t) = H - \frac{g t^{2}}{2}$ ,

где H — искомая высота; g = 10 м/с² — модуль ускорения свободного падения.

Пусть с начала падения до достижения телом высоты H/3 прошло время t₁. Тогда
$y (t_{1}) = \frac{H}{3}$ , или $y (t_{1}) = H - \frac{g t_{1}^{2}}{2} = \frac{H}{3}$ .

Отсюда следует, что тело окажется на высоте, равной H/3, через интервал времени

$t_{1} = \sqrt{\frac{4 H}{3 g}}$ .

Пусть с начала падения до достижения телом поверхности Земли прошло время t₂, тогда
y(t₂) = 0, или $y (t_{2}) = H - \frac{g t_{1}^{2}}{2} = 0$ .

Отсюда следует, что тело окажется на Земле через интервал времени

$t_{2} = \sqrt{\frac{2 H}{g}}$ .

Время движения тела с высоты H/3 до поверхности Земли определяется разностью:
∆t = t₂ − t₁

и составляет ∆t = 0,5 с (по условию задачи). Это позволяет записать уравнение, позволяющее определить высоту H:

$\sqrt{\frac{2 H}{g}} - \sqrt{\frac{4 H}{3 g}} = Δ t$ .

Для нахождения H преобразуем уравнение к виду

$\sqrt{\frac{2 H}{g}} (1 - \frac{\sqrt{2}}{\sqrt{3}}) = Δ t$ ,

возведем обе части в квадрат

$\frac{2 H}{g} {(1 - \frac{\sqrt{2}}{\sqrt{3}})}^{2} = Δ t^{2}$

и рассчитаем H:

$H = \frac{g Δ t^{2}}{2 {(1 - \frac{\sqrt{2}}{\sqrt{3}})}^{2}} \approx \frac{10 \cdot {(0,5)}^{2}}{0,067} \approx 37$ м.