Физика
Когерентные волны. Картина интерференции
Картина интерференции (чередование в пространстве темных и светлых полос, колец и т.п.) возникает при наложении двух когерентных волн.
Две волны называются когерентными, если:
1) они имеют одинаковые частоты (длины волн) и являются монохроматичными:
ν1 = ν2 = const,
где ν1 — частота первой волны; ν2 — частота второй волны;
2) в определенной точке пространства в произвольный момент времени разность фаз колебаний имеет фиксированное значение:
Δφ = |φ2 − φ1| = const,
где φ1 — фаза первой волны; φ2 — фаза второй волны;
3) колебания векторов напряженности электрических (и магнитных) полей в каждой из волн имеют одинаковые направления.
Когерентными источниками света называются источники, испускающие когерентные световые волны.
Интерференция световых волн — явление пространственного перераспределения энергии светового потока, возникающего при наложении двух когерентных волн, в результате чего в одних местах пространства появляются максимумы, а в других — минимумы интенсивности.
Картина интерференции — чередование интерференционных максимумов и минимумов на экране (или в других местах наблюдения), имеющее вид темных и светлых полос (колец и т.п.).
Для описания процесса распространения световой волны в среде и явления интерференции двух когерентных волн вводят следующие характеристики:
1) оптическая длина пути световой волны:
L = nS,
где n — показатель преломления среды, в которой распространяется волна; S — геометрическая длина пути световой волны;
2) оптическая разность хода двух когерентных волн (разность оптических длин, проходимых волнами путей):
Δ = L 2 − L 1,
где L 1 — оптическая длина пути первой волны; L 2 — оптическая длина пути второй волны.
При наложении двух когерентных волн происходит пространственное перераспределение световой энергии (явление интерференции): в одних местах пространства наблюдается усиление (максимумы) интенсивности светового потока, в других — ослабление (минимумы) интенсивности светового потока (картина интерференции).
Максимумы интерференции двух когерентных волн формируются, если оптическая разность хода двух волн равна четному числу длин полуволн в вакууме:
,
где m = 0, 1, 2, 3, ...; λ0 — длина световой волны в вакууме (воздухе); Δ — оптическая разность хода двух когерентных волн.
При m = 0 наблюдается центральный максимум; ему соответствует оптическая разность хода, равная нулю. При m = 1 наблюдается максимум первого порядка, при m = 2 — максимум второго порядка и т.п.
Минимумы интерференции двух когерентных волн формируются, если оптическая разность хода двух волн равна нечетному числу длин полуволн в вакууме:
.
При m = 0 наблюдается минимум первого порядка, при m = 1 — минимум второго порядка и т.п.
Разность фаз колебаний двух световых волн, интерферирующих в определенной точке пространства, может быть рассчитана по формуле
,
где λ0 — длина световой волны в вакууме (воздухе); Δ — оптическая разность хода двух когерентных волн.
Если в определенной точке пространства находится:
- максимум интерференции, то колебания, возбуждаемые в этой точке световыми волнами, будут происходить в одинаковой фазе, т.е. разность фаз колебаний составит 2π — для первого максимума интерференции, 4π — для второго, 6π — для третьего и т.п.;
- минимум интерференции, то колебания, возбуждаемые в этой точке пространства световыми волнами, будут происходить в противоположной фазе, т.е. разность фаз колебаний составит π для первого минимума интерференции, 3π — для второго, 5π — для третьего и т.п.
Пример 21. Оптическая разность хода двух когерентных световых волн для некоторой точки пространства составляет 1,00 мкм. В данной точке образуется интерференционный минимум третьего порядка. Найти длину световых волн в вакууме и разность фаз колебаний в этой точке.
Решение. Минимумы интерференции двух когерентных волн формируются в случае, если оптическая разность хода двух волн в некоторой точке пространства равна нечетному числу длин полуволн в вакууме
,
где Δ — оптическая разность хода двух когерентных волн; m = 2 (соответствует минимуму третьего порядка); λ0 — длина световой волны в вакууме (воздухе).
Условие минимума интерференции третьего порядка, записанное в явном виде
,
позволяет получить формулу для расчета длины волны света в вакууме:
.
Расчет дает значение:
.
Разность фаз колебаний двух световых волн, интерферирующих в определенной точке пространства, может быть рассчитана по формуле
.
Оптическую разность хода двух когерентных световых волн для интерференционного минимума третьего порядка
подставим в формулу для разности фаз колебаний и получим
рад.
Для минимума интерференции третьего порядка разность фаз колебаний составляет 5π рад.
Ширина полосы интерференции. Применение интерференции
Шириной полосы интерференции называется расстояние между двумя соседними максимумами (или между двумя соседними минимумами) на экране, на котором наблюдается картина интерференции.
Максимумы и минимумы интенсивности могут представлять собой полосы или кольца:
- светлые полосы (или кольца) соответствуют максимумам;
- темные полосы (или кольца) — минимумам интерференции.
Шириной полосы интерференции Δx (рис. 11.39) считается суммарная ширина одной светлой и одной темной полосы (или кольца); переходу от светлой полосы (максимума интерференции) к соседней темной полосе (минимуму) соответствует оптическая разность хода λ/2 (рис. 11.40).


Схема опыта Юнга по интерференции световых волн показана на рис. 11.41:
- вторичными когерентными источниками света S 1 и S 2 служат две узкие щели в диафрагме Д, поставленной на пути распространения света от точечного источника; расстояние между щелями равно d;
- на экране Э, расположенном на расстоянии l от диафрагмы, наблюдается чередование светлых и темных полос (картина интерференции); светлые полосы соответствуют максимумам интерференции, темные — минимумам.
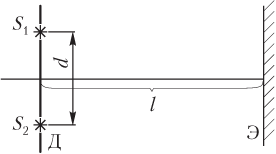
Ширина полосы интерференции определяется формулой
,
где l — расстояние от диафрагмы до экрана; d — расстояние между щелями (источниками света S 1 и S 2); λ — длина волны света в среде.
Важным обстоятельством для получения четкой картины интерференции является соблюдение условия d << l.
При решении задач об интерференции света на клине (рис. 11.42) следует помнить, что картина интерференции наблюдается на поверхности клина, а ширине полосы интерференции соответствует изменение толщины клина на величину
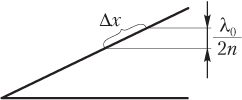
,
где λ — длина волны света в среде; λ0 — длина волны света в вакууме; n — показатель преломления материала клина (для воздушного клина n = 1).
Явление интерференции используется для просветления оптики, т.е. для уменьшения потерь света из-за отражений в оптических приборах. Для этого поверхности линз покрывают слоем прозрачного вещества, показатель преломления которого меньше показателя преломления материала линзы; толщина пленки определяется условием
,
где n — показатель преломления пленки; d — толщина пленки; m = 0, 1, 2, 3, ...; λ0 — та длина волны света в вакууме, для работы с которой предназначены линзы.
Минимальная толщина пленки определяется условием m = 0 и рассчитывается с помощью формулы
.
Пример 22. В опыте Юнга используется источник монохроматического света с длиной волны 600 нм. Щели диафрагмы, служащие вторичными источниками света, расположены на расстоянии 200 мкм друг от друга. Расстояние между диафрагмой и экраном, на котором наблюдают картину интерференции, увеличивают на 60,0 мм. Найти изменение ширины полосы интерференции.
Решение. На рисунке показана схема опыта Юнга и обозначены соответствующие расстояния: S 1 и S 2 — две узкие щели в диафрагме Д, поставленной на пути распространения света от точечного источника; расстояние между щелями равно d; Э — экран, расположенный на расстоянии l от диафрагмы.
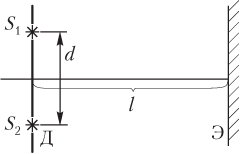
Ширина полосы интерференции, наблюдаемой на экране, описывается следующими формулами:
- для первого случая —
,
где l 1 — первоначальное расстояние от диафрагмы до экрана; d — расстояние между щелями, d = 200 мкм; λ — длина световой волны, λ = 600 нм;
- для второго случая —
,
где l 2 — новое расстояние от диафрагмы до экрана.
При увеличении расстояния l ширина полосы интерференции ∆x также увеличивается:
,
где Δl — увеличение расстояния от диафрагмы до экрана, Δl = l 2 − l 1.
Рассчитаем:
.
Пример 23. Для просветления линз оптических приборов используют напыление пленки с показателем преломления 1,25. Приборы предназначены для работы со светом, имеющим в вакууме длину волны 700 нм. Найти минимальную толщину покрытия, обеспечивающего просветление линз.
Решение. Для уменьшения потерь света в оптических приборах (просветление оптики) поверхности линз покрывают слоем прозрачного вещества, показатель преломления которого должен быть меньше показателя преломления материала линзы.
Толщина пленки определяется условием минимумов интерференции:
,
где n — показатель преломления материала пленки, n = 1,25; d — толщина пленки; m = 0, 1, 2, 3, ...; λ0 — длина световой волны в вакууме (воздухе), λ0 = 700 нм.
Минимальная толщина пленки определяется условием m = 0 (первый минимум интерференции):
и рассчитывается с помощью формулы
.
Вычислим:
.
Нанесение покрытия толщиной 140 нм обеспечит просветление линз при работе со светом указанной длины волны.










