Репетитор-онлайн — подготовка к ЦТ

11.3. Волновая оптика

11.3.3. Дифракция световых волн

Явление дифракции. Дифракционная картина, наблюдаемая с помощью дифракционной решетки

Дифракция — огибание волнами препятствий, встречающихся на их пути, или отклонение распространения волн вблизи препятствий от направления, предписанного законами геометрической оптики.

Явление дифракции световых волн имеет некоторые особенности возникновения и наблюдения:

явление дифракции имеет место, если длина световой волны λ достаточно мала по сравнению с размерами препятствий d, встречающихся на пути света:

λ << d;

дифракционная картина (т.е. отклонение распределения освещенности на экране от предсказанного геометрической оптикой) наблюдается только на расстояниях

$l \geq \frac{d^{2}}{λ}$ .

Объяснение дифракционных явлений дает принцип Гюйгенса — Френеля, согласно которому:

1) любая точка волновой поверхности рассматривается как источник вторичных сферических волн;

2) световые колебания в некоторой точке наблюдения есть результат сложения колебаний, вызванных вторичными волнами (с учетом их амплитуд и фаз);

3) результат сложения (усиление или ослабление света, светлая или темная область) в определенной точке пространства зависит только от амплитуд и фаз вторичных волн и не зависит от стандартных предсказаний геометрической оптики (тень или свет);

4) светлая область может оказаться в области геометрической тени (создается иллюзия огибания светом препятствий), а темная — там, где пролегает прямолинейный путь света.

Большое практическое значение имеет дифракционная картина, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

На рис. 11.43 схематично показано формирование дифракционной картины, полученной на некотором экране при прохождении света через дифракционную решетку:

Рис. 11.43

период (постоянная) дифракционной решетки d есть сумма:

d = a + b,

где a — ширина щели (прозрачного промежутка); b — ширина непрозрачного промежутка;

угол дифракции φ — угол отклонения света от прямолинейного направления;
оптическая разность хода двух лучей, идущих от соседних щелей:

Δ = d sin φ.

Дифракционная картина, образованная дифракционной решеткой, есть результат взаимной интерференции волн, идущих от всех щелей.

Наблюдаемая на экране дифракционная картина имеет следующий вид:

в центре экрана расположен главный максимум интенсивности (белого цвета);
по обе стороны, симметрично от главного максимума, — ряд окрашенных максимумов меньшей интенсивности, разделенных дифракционными минимумами.

Световая энергия в дифракционной картине распределена следующим образом:

ее основная часть сосредоточена в центральном максимуме;
остальные максимумы имеют существенно меньшую интенсивность.

Яркость дифракционной картины и количество наблюдаемых максимумов на экране зависит от ширины щели:

сужение щели приводит к уменьшению яркости картины дифракции и уменьшению количества наблюдаемых максимумов;
расширение щели вызывает увеличение яркости картины дифракции и увеличение количества наблюдаемых максимумов.

Дифракционная решетка разлагает белый свет в спектр:

центральный максимум является белым, т.е. не окрашен;
первые максимумы (ближайшие к центральному максимуму) получаются фиолетовыми;
вторые — синими и т.п.

Наименьшее отклонение от прямолинейного распространения имеют световые волны с наименьшей длиной волны (фиолетовый свет), наибольшее — с наибольшей длиной волны (красный свет).

Дифракционные максимумы наблюдаются при выполнении условия

d sin φ = mλ,

где d sin φ = Δ — оптическая разность хода двух лучей, идущих от соседних щелей; m = 0 соответствует центральному максимуму интенсивности; m = ±1 — первым максимумам; m = ±2 — вторым максимумам; m = ±3 — третьим максимумам и т.п.

Пример 24. При нормальном освещении дифракционной решетки светом с длиной волны 500 нм максимум второго порядка образуется под углом 30°. Найти длину волны света, при освещении которым той же дифракционной решетки максимум третьего порядка образуется под углом 45°.

Решение. При нормальном падении плоской монохроматической световой волны на дифракционную решетку на экране формируется дифракционная картина, максимумы которой определяются условием:

в первом случае (λ = 500 нм) —

d sin φ₁ = m ₁λ₁,

где d — период дифракционной решетки; φ₁ — угол дифракции для максимума второго порядка, φ₁ = 30°; m ₁ — номер дифракционного максимума, m ₁ = 2;

во втором случае (λ₂ — искомая длина волны) —

d sin φ₂ = m ₂λ₂,

где φ₂ — угол дифракции для максимума третьего порядка, φ₂ = 45°; m ₂ — номер дифракционного максимума, m ₂ = 3.

Деление уравнений дает:

$\frac{\sin φ_{1}}{\sin φ_{2}} = \frac{m_{1} λ_{1}}{m_{2} λ_{2}}$ .

Выразим отсюда искомую величину

$λ_{2} = \frac{m_{1} λ_{1} \sin φ_{2}}{m_{2} \sin φ_{1}}$

и вычислим:

$λ_{2} = \frac{2 \cdot 500 \cdot 10^{- 9} \sin 45 °}{3 \cdot \sin 30 °} = 470 \cdot 10^{- 9} м = 470 нм$ .

Искомая длина волны составляет 470 нм.

Условие дифракционных максимумов. Особенности его применения к решению задач

При решении задач о дифракционных решетках пользуются условием дифракционных максимумов

d sin φ = mλ,

где d — период дифракционной решетки; φ — угол дифракции; m = 0 соответствует центральному максимуму; m = ±1 — первым максимумам; m = ±2 — вторым максимумам; m = ±3 — третьим максимумам; λ — длина волны падающего на решетку света.

При этом следует помнить, что:

угол дифракции φ совпадает с углом между направлениями на центральный максимум и на максимум с номером m (рис. 11.44);
угол между направлениями на два максимума одного порядка (например, угол θ между первыми максимумами, вторыми и т.п.) равен удвоенному углу дифракции (см. рис. 11.44):

θ = 2φ.

Рис. 11.44

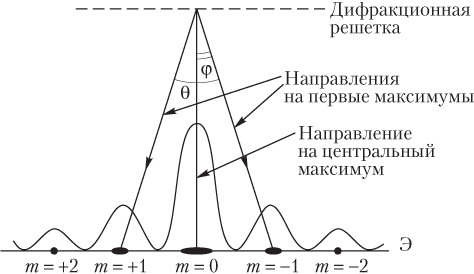
Угол дифракции φ зависит от длины волны падающего света. Он имеет:

минимальное значение для световых волн, длина волны которых соответствует фиолетовому свету;
максимальное значение для световых волн, длина волны которых соответствует красному свету.

При нахождении максимального порядка дифракционного спектра необходимо учитывать следующее:

максимальный угол отклонения лучей дифракционной решеткой равен

φ_max = 90°;

вычисления следует производить по формуле

$m_{max} = \frac{d}{λ}$ ,

где d — период дифракционной решетки;

после вычисления m _max по приведенной выше формуле нужно оставить целую часть полученного числа.

При нахождении максимального количества дифракционных максимумов, которое можно наблюдать на экране с помощью данной дифракционной решетки, необходимо:

определить максимальный порядок дифракционного спектра m _max по соответствующему алгоритму, т.е. рассчитать целую часть выражения

$m_{max} = [\frac{d}{λ}]$ ,

где d — период дифракционной решетки; λ — длина световой волны;

вычислить искомое количество дифракционных максимумов по формуле

k = 2m _max + 1,

где m _max — целая часть отношения d/λ.

Следует отметить, что данная формула учитывает одинаковое количество дифракционных максимумов по обе стороны от центрального и еще один максимум — центральный.

Иногда в задачах вместо периода дифракционной решетки задано количество штрихов на единицу длины.

Для определения периода дифракционной решетки в этом случае пользуются формулой

$d = \frac{L}{N}$ ,

где N — число штрихов, нанесенных на участок дифракционной решетки длиной L.

Пример 25. На дифракционную решетку с периодом 2,50 мкм падает нормально плоская монохроматическая волна. Найти количество дифракционных максимумов, если длина световой волны составляет 700 нм.

Решение. Дифракционная картина, образованная дифракционной решеткой, имеет следующий вид:

в центре экрана расположен главный максимум интенсивности;
по обе стороны от него расположены несколько дифракционных максимумов, разделенных дифракционными минимумами.

Максимальный порядок дифракционного максимума, который можно увидеть с помощью данной решетки, определяется условием

$m_{max} = [\frac{d}{λ}]$ ,

где d — период дифракционной решетки, d = 2,50 мкм; λ — длина волны падающего на решетку света.

Расчет дает значение

$m = \frac{d}{λ} = \frac{2,50 \cdot 10^{- 6}}{700 \cdot 10^{- 9}} = 3,57$ .

Для определения максимального порядка следует взять целую часть от расчетного значения:

m _max = [3,57] = 3.

Следовательно, по обе стороны от центрального расположено по три максимума.

Количество дифракционных максимумов на экране рассчитаем по формуле

k = 2m _max + 1 = 2 ⋅ 3 + 1 = 7.

Дифракционный спектр содержит 7 максимумов.

Пример 26. Дифракционная решетка с периодом 10 мкм освещается белым светом. Свет падает на решетку нормально, а длины волн белого света заключены в интервале от 0,38 до 0,76 мкм. На расстоянии 3,1 м от решетки расположен экран. Определить ширину спектра первого порядка.

Решение. Световые волны с различными длинами волн отклоняются дифракционной решеткой по-разному. Угол дифракции первого порядка (m = 1) определяется условиями:

для длины волны λ₁ = 0,38 мкм —

d sin φ₁ = λ₁,

где d — период дифракционной решетки, d = 10 мкм; φ₁ — угол дифракции для максимума первого порядка при освещении решетки светом с длиной волны λ₁;

для длины волны λ₂ = 0,76 мкм —

d sin φ₂ = λ₂,

где φ₂ — угол дифракции для максимума первого порядка при освещении решетки светом с длиной волны λ₂.

Ширина спектра первого порядка — расстояние между указанными максимумами.

На рисунке показаны расстояния x ₁ и x ₂:

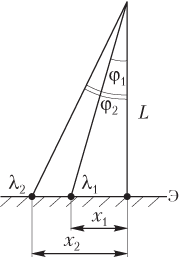
x ₁ представляет собой расстояние от центра экрана (центрального максимума) до максимума первого порядка для длины волны λ₁;
x ₂ представляет собой расстояние от центра экрана (центрального максимума) до максимума первого порядка для длины волны λ₂.

Ширина спектра первого порядка является разностью указанных расстояний:

Δx = x ₂ − x ₁.

Из построения следует, что

x ₁ = L tg φ₁ и x ₂ = L tg φ₂,

где L — расстояние от дифракционной решетки до экрана, L = 3,1 м.

Следовательно, искомая разность имеет вид

Δx = L(tg φ₂ − tg φ₁).

Тангенсы углов дифракции связаны с синусами указанных углов формулой

$tg φ = \frac{\sin φ}{\sqrt{1 - {sin}^{2} φ}}$ .

Поэтому

$Δ x = L (\frac{\sin φ_{2}}{\sqrt{1 - {sin}^{2} φ_{2}}} - \frac{\sin φ_{1}}{\sqrt{1 - {sin}^{2} φ_{1}}})$ .

Синусы углов дифракции найдем из условий дифракционных максимумов первого порядка:

для длины волны λ₁ —

$\sin φ_{1} = \frac{λ_{1}}{d}$ ;

для длины волны λ₂ —

$\sin φ_{2} = \frac{λ_{2}}{d}$ .

Подставим записанные отношения в формулу для расчета ширины спектра

$Δ x = L (\frac{λ_{2} / d}{\sqrt{1 - {(λ_{2} / d)}^{2}}} - \frac{λ_{1} / d}{\sqrt{1 - {(λ_{1} / d)}^{2}}})$

и вычислим:

$Δ x = 3,1 \cdot (\frac{0,76 / 10}{\sqrt{1 - {(0,76 / 10)}^{2}}} - \frac{0,38 / 10}{\sqrt{1 - {(0,38 / 10)}^{2}}}) = 12 \cdot 10^{- 2} м = 12 см$ .

Ширина спектра первого порядка на экране составляет 12 см.

Физика