Физика
Формирование изображения в плоском зеркале и его свойства
Законы отражения, преломления и прямолинейного распространения света используются при построении изображений в зеркалах, рассмотрении хода световых лучей в плоскопараллельной пластинке, призме и линзах.
Ход световых лучей в плоском зеркале показан на рис. 11.10.

Изображение в плоском зеркале формируется за плоскостью зеркала на том же расстоянии от зеркала f, на каком находится предмет перед зеркалом d:
f = d.
Изображение в плоском зеркале является:
- прямым;
- мнимым;
- равным по величине предмету: h = H.
Если плоские зеркала образуют между собой некоторый угол, то они формируют N изображений источника света, помещенного на биссектрису угла между зеркалами (рис. 11.11):
,
где γ — угол между зеркалами (в радианах).
Примечание. Формула справедлива для таких углов γ, для которых отношение 2π/γ является целым числом.Например, на рис. 11.11 показан источник света S, лежащий на биссектрисе угла π/3. Согласно приведенной выше формуле формируются пять изображений:
1) изображение S1 формируется зеркалом 1;
2) изображение S2 формируется зеркалом 2;

3) изображение S3 является отражением S1 в зеркале 2;
4) изображение S4 является отражением S2 в зеркале 1;
5) изображение S5 является отражением S3 в продолжении зеркала 1 или отражением S4 в продолжении зеркала 2 (отражения в указанных зеркалах совпадают).
Пример 8. Найти число изображений точечного источника света, полученных в двух плоских зеркалах, образующих друг с другом угол 90°. Источник света находится на биссектрисе указанного угла.
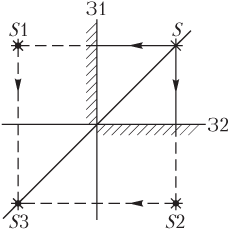
Решение. Выполним рисунок, поясняющий условие задачи:
- источник света S расположен на биссектрисе угла между зеркалами;
- первое (вертикальное) зеркало З1 формирует изображение S1;
- второе (горизонтальное) зеркало З2 формирует изображение S2;
- продолжение первого зеркала формирует изображение мнимого источника S2, а продолжение второго зеркала — мнимого источника S1; указанные изображения совпадают и дают S3.
Число изображений источника света, помещенного на биссектрису угла между зеркалами, определяется формулой
,
где γ — угол между зеркалами (в радианах), γ = π/2.
Число изображений составляет
.
Ход светового луча в плоскопараллельной пластинке
Ход светового луча в плоскопараллельной пластинке зависит от оптических свойств среды, в которой находится пластинка.
1. Ход светового луча в плоскопараллельной пластинке, находящейся в оптически однородной среде (по обе стороны от пластинки коэффициент преломления среды одинаков), показан на рис. 11.12.
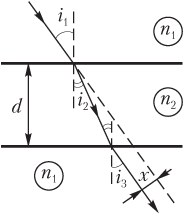
Световой луч, падающий на плоскопараллельную пластинку под некоторым углом i 1, после прохождения плоскопараллельной пластинки:
- выходит из нее под тем же углом:
i 3 = i 1;
- смещается на величину x от первоначального направления (пунктир на рис. 11.12).
2. Ход светового луча в плоскопараллельной пластинке, находящейся на границе двух сред (по обе стороны от пластинки коэффициенты преломления сред различны), показан на рис. 11.13 и 11.14.
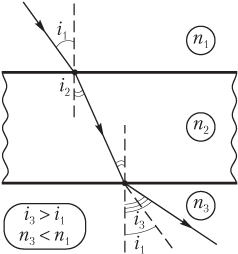
Световой луч после прохождения плоскопараллельной пластинки выходит из пластинки под углом, отличающимся от угла падения его на пластинку:
- если показатель преломления среды за пластинкой меньше показателя преломления среды перед пластинкой (n 3 < n 1), то:
i 3 > i 1,
т.е. луч выходит под бо́льшим углом (см. рис. 11.13);
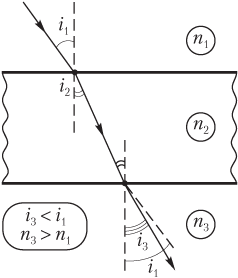
- если показатель преломления среды за пластинкой больше показателя преломления среды перед пластинкой (n 3 > n 1), то:
i 3 < i 1,
т.е. луч выходит под меньшим углом (см. рис. 11.14).
Смещение луча — длина перпендикуляра между выходящим из пластинки лучом и продолжением луча, падающего на плоскопараллельную пластинку.
Смещение луча при выходе из плоскопараллельной пластинки, находящейся в оптически однородной среде (см. рис. 11.12), рассчитывается по формуле
,
где d — толщина плоскопараллельной пластинки; i 1 — угол падения луча на плоскопараллельную пластинку; n — относительный показатель преломления материала пластинки (относительно той среды, в которую помещена пластинка), n = n 2/n 1; n 1 — абсолютный показатель преломления среды; n 2 — абсолютный показатель преломления материала пластинки.

Смещение луча при выходе из плоскопараллельной пластинки может быть рассчитано с помощью следующего алгоритма (рис. 11.15):
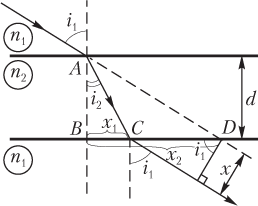
1) вычисляют x 1 из треугольника ABC, пользуясь законом преломления света:
n 1 sin i 1 = n 2 sin i 2,
где n 1 — абсолютный показатель преломления среды, в которую помещена пластинка; n 2 — абсолютный показатель преломления материала пластинки;
2) вычисляют x 2 из треугольника ABD;
3) рассчитывают их разность:
Δx = x 2 − x 1;
4) смещение находят по формуле
x = Δx cos i 1.
Время распространения светового луча в плоскопараллельной пластинке (рис. 11.15) определяется формулой
,
где S — путь, пройденный светом, ; v — скорость распространения светового луча в материале пластинки, v = c/n; c — скорость света в вакууме, c ≈ 3 ⋅ 108 м/с; n — показатель преломления материала пластинки.
Путь, пройденный световым лучом в пластинке, связан с ее толщиной выражением
S = d cos i 2,
где d — толщина пластинки; i 2 — угол преломления светового луча в пластинке.
Пример 9. Угол падения светового луча на плоскопараллельную пластинку равен 60°. Пластинка имеет толщину 5,19 см и изготовлена из материала с показателем преломления 1,73. Найти смещение луча при выходе из плоскопараллельной пластинки, если она находится в воздухе.
Решение. Выполним рисунок, на котором покажем ход светового луча в плоскопараллельной пластинке:
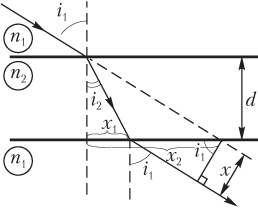
- световой луч падает на плоскопараллельную пластинку под углом i 1;
- на границе раздела воздуха и пластинки луч преломляется; угол преломления светового луча равен i 2;
- на границе раздела пластинки и воздуха луч преломляется еще раз; угол преломления равен i 1.
Указанная пластинка находится в воздухе, т.е. по обе стороны от пластинки среда (воздух) имеет одинаковый показатель преломления; следовательно, для расчета смещения луча можно применить формулу
,
где d — толщина пластинки, d = 5,19 см; n — показатель преломления материала пластинки относительно воздуха, n = 1,73; i 1 — угол падения света на пластинку, i 1 = 60°.
Вычисления дают результат:
.
Cмещение луча света при выходе из плоскопараллельной пластинки равно 3 см.
Ход светового луча в призме
Ход светового луча в призме показан на рис. 11.16.

Грани призмы, через которые проходит луч света, называются преломляющими. Угол между преломляющими гранями призмы называется преломляющим углом призмы.
Световой луч после прохождения через призму отклоняется; угол между лучом, выходящим из призмы, и лучом, падающим на призму, называется углом отклонения луча призмой.
Угол отклонения луча призмой φ (см. рис. 11.16) представляет собой угол между продолжениями лучей I и II — на рисунке обозначены пунктиром и символом (I), а также пунктиром и символом (II).
1. Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
φ = i 1 + i 2 − θ,
где i 1 — угол падения луча на преломляющую грань призмы (угол между лучом и перпендикуляром к преломляющей грани призмы в точке падения луча); i 2 — угол выхода луча из призмы (угол между лучом и перпендикуляром к грани призмы в точке выхода луча); θ — преломляющий угол призмы.
2. Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярно преломляющей грани призмы), то угол отклонения луча призмой определяется формулой
φ = θ(n − 1),
где θ — преломляющий угол призмы; n — относительный показатель преломления материала призмы (относительно той среды, в которую эта призма помещена), n = n 2/n 1; n 1— показатель преломления среды, n 2 — показатель преломления материала призмы.
Вследствие явления дисперсии (зависимость показателя преломления от частоты светового излучения) призма разлагает белый свет в спектр (рис. 11.17).

Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.
Пример 10. Стеклянная призма, изготовленная из материала с коэффициентом преломления 1,2, имеет преломляющий угол 46° и находится в воздухе. Луч света падает из воздуха на преломляющую грань призмы под углом 30°. Найти угол отклонения луча призмой.
Решение. Выполним рисунок, на котором покажем ход светового луча в призме:
- световой луч падает из воздуха под углом i 1 = 30° на первую преломляющую грань призмы и преломляется под углом i 2;
- световой луч падает под углом i 3 на вторую преломляющую грань призмы и преломляется под углом i 4.

Угол отклонения луча призмой определяется формулой
φ = i 1 + i 4 − θ,
где θ — преломляющий угол призмы, θ = 46°.
Для расчета угла отклонения светового луча призмой необходимо вычислить угол выхода луча из призмы.
Воспользуемся законом преломления света для первой преломляющей грани
n 1 sin i 1 = n 2 sin i 2,
где n 1 — показатель преломления воздуха, n 1 = 1; n 2 — показатель преломления материала призмы, n 2 = 1,2.
Рассчитаем угол преломления i 2:
i 2 = arcsin (n 1 sin i 1/n 2) = arcsin(sin 30°/1,2) = arcsin(0,4167);
i 2 ≈ 25°.
Из треугольника ABC
α + β + θ = 180°,
где α = 90° − i 2; β = 90° − i 3; i 3 — угол падения светового луча на вторую преломляющую грань призмы.
Отсюда следует, что
i 3 = θ − i 2 ≈ 46° − 25° = 21°.
Воспользуемся законом преломления света для второй преломляющей грани
n 2 sin i 3 = n 1 sin i 4,
где i 4 — угол выхода луча из призмы.
Рассчитаем угол преломления i 4:
i 4 = arcsin (n 2 sin i 3/n 1) = arcsin(1,2 ⋅ sin 21°/1,0) = arcsin(0,4301);
i 4 ≈ 26°.
Угол отклонения луча призмой составляет
φ = 30° + 26° − 46° = 10°.










