Репетитор-онлайн — подготовка к ЦТ

11.2. Геометрическая оптика

11.2.1. Законы геометрической оптики

Закон прямолинейного распространения света: в прозрачной однородной среде свет распространяется прямолинейно.

Закон независимости световых лучей: распространение двух световых лучей в однородной среде происходит независимо друг от друга.

При освещении непрозрачного предмета AB точечным источником света S на экране образуется тень A′B′ с резкими границами (рис. 11.1).

Рис. 11.1

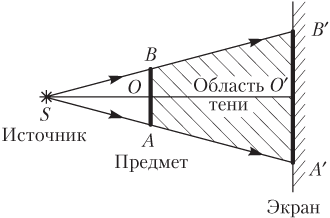
Линейный размер тени на экране превышает размер предмета в k раз, т.е.

$k = \frac{| A^{'} B^{'} |}{| A B |} = \frac{| S O^{'} |}{| S O |}$ ,

где |AB| — линейный размер предмета; |A′B′| — линейный размер изображения; |SO| — расстояние от источника до предмета; |SO′| — расстояние от источника до экрана.

Размер площади тени (рис. 11.1) превышает площадь предмета (квадрата, диска и т.п.), плоскость АВ которого расположена перпендикулярно лучу SO, в k ² раз, т.е.

$k^{2} = {(\frac{| A^{'} B^{'} |}{| A B |})}^{2} = {(\frac{| S O^{'} |}{| S O |})}^{2}$ .

Пример 1. Человек, рост которого 1,7 м, идет со скоростью 1,0 м/с по направлению к уличному фонарю. В некоторый момент длина тени была 1,8 м, а через 2,0 с стала 1,3 м. На какой высоте висит фонарь?

Решение. Выполним иллюстрацию к условию задачи. На рисунках показаны два положения человека (стрелка) по отношению к уличному фонарю S, подвешенному на фонарном столбе высотой H:

на рис. а человек ростом h находится на расстоянии x ₁ от основания фонарного столба; длина тени человека — l ₁;
на рис. б — на расстоянии x ₂ от основания фонарного столба; длина тени человека — l ₂.

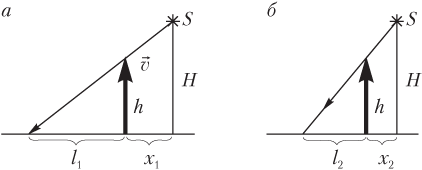
Расстояния от человека до фонарного столба связаны между собой разностью

x ₂ = x ₁ − vt,

где v — модуль скорости движения человека; t — интервал времени, за который расстояние уменьшается от x ₁ до x ₂.

Подобие треугольников на каждом из рисунков позволяет записать следующие отношения:

для рис. а —

$\frac{l_{1} + x_{1}}{H} = \frac{l_{1}}{h}$ ;

для рис. б —

$\frac{l_{2} + x_{2}}{H} = \frac{l_{2}}{h}$ .

Записанные уравнения образуют систему

$\begin{array}{l} x_{2} = x_{1} - v t, \\ \frac{l_{1} + x_{1}}{H} = \frac{l_{1}}{h}, \\ \frac{l_{2} + x_{2}}{H} = \frac{l_{2}}{h}, \end{array}}$

которую требуется решить относительно величины H.

Для этого выразим из второго и третьего уравнения системы x ₁ и x ₂:

$x_{1} = \frac{l_{1} (H - h)}{h}$ , $x_{2} = \frac{l_{2} (H - h)}{h}$ .

Подставим x ₁ и x ₂ в первое уравнение системы:

$\frac{l_{2} (H - h)}{h} = \frac{l_{1} (H - h)}{h} - v t$ .

Выразим отсюда искомую величину:

$H = h (1 + \frac{v t}{l_{1} - l_{2}})$ .

Вычислим:

$H = 1,7 \cdot (1 + \frac{1,0 \cdot 2,0}{1,8 - 1,3}) = 8,5$ м.

Фонарь висит на высоте 8,5 м.

Отражение света от границы двух сред

Закон отражения света: луч падающий (I), луч отраженный (II) и перпендикуляр к границе раздела двух сред, восстановленный в точке падения светового луча, лежат в одной плоскости (рис. 11.2); угол отражения равен углу падения:

${i^{'}}_{1} = i_{1}$ ,

где i ₁ — угол падения; ${i^{'}}_{1}$ — угол отражения.

Рис. 11.2

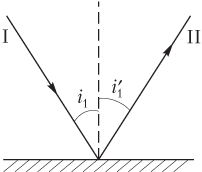
Угол падения — угол между падающим лучом и перпендикуляром к поверхности (а не поверхностью!).

Угол отражения — угол между отраженным лучом и перпендикуляром к поверхности (а не поверхностью!).

Если луч отражается от плоского зеркала, то:

1) при повороте плоского зеркала на угол φ отраженный от него луч поворачивается на угол

φ′ = 2φ,

где φ — угол поворота зеркала; φ′ — угол поворота отраженного луча;

2) при вращении зеркала:

с угловой скоростью ω отраженный от него луч вращается с угловой скоростью

ω′ = 2ω,

где ω — угловая скорость вращения зеркала; ω′ — угловая скорость отраженного луча;

с частотой ν отраженный от него луч вращается с частотой

ν′ = 2ν,

где ν — частота вращения зеркала; ν′ — частота вращения отраженного луча.

Пример 2. Зеркало повернули на угол 30° относительно оси, проходящей через его плоскость. Найти угол (в градусах) поворота луча, отраженного зеркалом. Направление падающего на зеркало луча постоянно.

Решение. Выполним иллюстрацию к условию задачи. На рисунках показаны два луча — падающий (I) и отраженный (II и III):

на рис. а луч I падает под углом α на зеркало, лежащее горизонтально; луч II отражается от зеркала под углом α′;
на рис. б луч I падает в том же направлении, однако угол падения его на зеркало изменяется (за счет поворота зеркала на угол γ) и составляет β; луч III отражается от зеркала под углом β′.

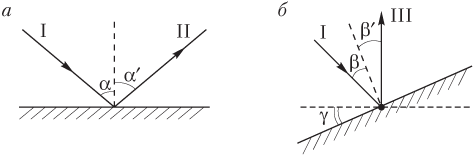
Согласно закону отражения света углы падения и отражения одинаковы:

для рис. а —

α′ = α;

для рис. б —

β′ = β.

Сумма углов падения и отражения представляет собой угол между лучом падающим и лучом отраженным и составляет:

для рис. а —

φ₁ = 2α,

где φ₁ — угол между лучами I и II;

для рис. б —

φ₂ = 2β,

где φ₂ — угол между лучами I и III.

Угол поворота отраженного луча представляет собой разность углов φ₁ и φ₂:

Δφ = φ₁ − φ₂ = 2(α − β).

Найдем разность между углами α и β.

Нормаль (перпендикуляр) к поверхности зеркала в точке падения светового луча при повороте зеркала на угол γ также поворачивается на угол γ. Из построения следует, что угол падения светового луча при показанном на рисунке направлении поворота зеркала уменьшается на такую же величину:

β = α − γ.

Следовательно, искомый угол поворота отраженного луча составляет:

Δφ = 2(α − (α − γ)) = 2γ = 2 ⋅ 30° = 60°.

Преломление света на границе двух сред

Закон преломления света: луч падающий (I), луч преломленный (II) и перпендикуляр к границе раздела двух сред, восстановленный в точке падения светового луча, лежат в одной плоскости (рис. 11.3); угол падения и угол преломления связаны между собой соотношением

Рис. 11.3

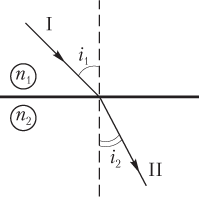
n ₁ sin i ₁ = n ₂ sin i ₂,

где n ₁ — абсолютный показатель преломления первой среды; n ₂ — абсолютный показатель преломления второй среды.

Угол преломления — угол между преломленным лучом и перпендикуляром к поверхности (а не поверхностью!).

Преломленный луч:

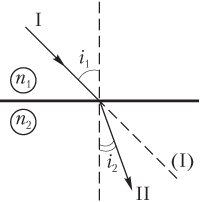
1) «прижимается» к нормали (перпендикуляру), если свет идет из среды с меньшей оптической плотностью (меньшим показателем преломления n ₁) в среду с большей оптической плотностью (бо́льшим показателем преломления n ₂) (рис. 11.4):

n ₁ < n ₂;

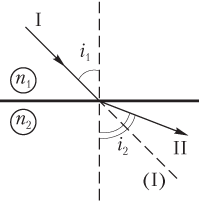
2) «отклоняется» от нормали (перпендикуляра), если свет идет из среды с большей оптической плотностью (бо́льшим показателем преломления n ₁) в среду с меньшей оптической плотностью (меньшим показателем преломления n ₂) (рис. 11.5):

n ₁ > n ₂.

Рис. 11.4

Рис. 11.5

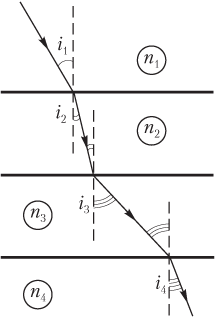
Если луч света испытывает несколько преломлений (преломленный луч после выхода из второй среды попадает в третью среду, а затем в четвертую и т.п.), то закон преломления записывают в виде (рис. 11.6):

n ₁ sin i ₁ = n ₂ sin i ₂ = n ₃ sin i ₃ = n ₄ sin i ₄ = ...,

где n ₁ — абсолютный показатель преломления первой среды; n ₂ — абсолютный показатель преломления второй среды; n ₃ — абсолютный показатель преломления третьей среды; n ₄ — абсолютный показатель преломления четвертой среды и т.п.; i ₁ — угол падения луча; i ₂ — угол преломления луча во второй среде; i ₃ — угол преломления луча в третьей среде; i ₄ — угол преломления луча в четвертой среде и т.п.

Рис. 11.6

Пример 3. Луч света падает из воздуха на плоскопараллельную стеклянную пластинку под углом 45°, а из стекла попадает в жидкость с показателем преломления 1,41. Найти угол преломления света в жидкости.

Решение. Запишем закон преломления света в следующем виде:

n ₁ sin i ₁ = n ₂ sin i ₂ = n ₃ sin i ₃,

где n ₁ — показатель преломления воздуха, n ₁ = 1; i ₁ — угол падения луча на плоскопараллельную пластинку, i ₁ = 45°; n ₂ — показатель преломления стекла; i ₂ — угол преломления света в стекле; n ₃ — показатель преломления жидкости, n ₃ = 1,41; i ₃ — угол преломления света в жидкости (искомая величина).

Преобразуем записанное выражение к виду

n ₁ sin i ₁ = n ₃ sin i ₃

и выразим синус искомого угла:

$\sin i_{3} = \frac{n_{1}}{n_{3}} \sin i_{1} = \frac{n_{1}}{n_{3}} \sin 45 °$ .

Расчет дает значение:

$\sin i_{3} = \frac{1}{1,41} \cdot \frac{\sqrt{2}}{2} = 0,5$ .

Следовательно, искомый угол составляет

i ₃ = arcsin 0,5 = 30°.

Пример 4. Узкий световой пучок падает из среды с показателем преломления 1,25 на границу ее раздела со средой, имеющей показатель преломления 1,75. На границе раздела происходит частичное отражение светового пучка, а часть светового пучка, преломляясь, переходит во вторую среду. Известно, что угол между отраженным и преломленным лучами составляет 90°. Определить тангенс угла падения светового луча на границу раздела двух сред.

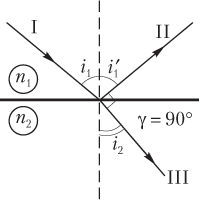
Решение. Рисунок поясняет условие задачи:

луч I падает на границу раздела двух сред под углом i ₁;
луч II отражается от границы раздела двух сред под углом ${i^{'}}_{1}$ ;
луч III преломляется на границе раздела двух сред под углом i ₂.

Указанные углы связаны между собой законами отражения и преломления света:

углы падения и отражения — законом отражения —

$i_{1} = {i^{'}}_{1}$ ,

где i ₁ — угол падения светового луча на границу раздела двух сред; ${i^{'}}_{1}$ — угол отражения светового луча от границы двух сред;

углы падения и преломления — законом преломления —

n ₁ sin i ₁ = n ₂ sin i ₂,

где n ₁ — коэффициент преломления первой среды, n ₁ = 1,25; n ₂ — коэффициент преломления второй среды, n ₂ = 1,75; i ₂ — угол преломления светового луча на границе раздела двух сред.

Из построения следует, что угол

${i^{'}}_{1} + γ + i_{2} = 180 °$ ,

где γ — угол между отраженным II и преломленным III лучами, γ = 90° (по условию задачи).

Следовательно,

${i^{'}}_{1} + i_{2} = 90 °$ , или i ₁ + i ₂ = 90°.

Записанное равенство, закон преломления и определение тангенса угла падения образуют систему уравнений

$\begin{array}{l} i_{1} + i_{2} = 90 °, \\ n_{1} \sin i_{1} = n_{2} \sin i_{2}, \\ tg i_{1} = \frac{\sin i_{1}}{\cos i_{1}}, \end{array}}$

которую необходимо решить относительно функции, определяемой третьим уравнением, т.е. tg i ₁.

Из первого уравнения системы следует, что

i ₂ = 90° − i ₁.

Подставим i ₂ во второе уравнение

n ₁ sin i ₁ = n ₂ sin(90° − i ₁)

и преобразуем полученное выражение, пользуясь тождеством

sin(90° − i ₁) = cos i ₁,

к виду

n ₁ sin i ₁ = n ₂ cos i ₁.

Отсюда следует, что

$\frac{\sin i_{1}}{\cos i_{1}} = \frac{n_{2}}{n_{1}}$ .

Подстановка полученного отношения в третье уравнение системы позволяет получить результат:

$tg i_{1} = \frac{n_{2}}{n_{1}} = \frac{1,75}{1,25} = 1,40$ .

Пример 5. Самолет пролетает над погрузившейся на небольшую глубину подводной лодкой на высоте 1,5 км. Какой кажется высота полета при наблюдении с лодки? Показатель преломления воды равен 4/3.

Решение. Проиллюстрируем условие задачи:

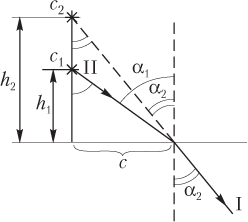
истинная (реальная) высота самолета c ₁ над поверхностью Земли обозначена h ₁;
кажущаяся высота самолета c ₂ — h ₂;
продолжение луча I обозначено пунктиром.

Из построения следует:

для луча II —

$tg α_{1} = \frac{c}{h_{1}}$ ,

где c — расстояние, показанное на рисунке (общий катет треугольников);

для продолжения луча I —

$tg α_{2} = \frac{c}{h_{2}}$ .

Отсюда следует, что

$\frac{tg α_{1}}{tg α_{2}} = \frac{c}{h_{1}} \cdot \frac{h_{2}}{c} = \frac{h_{2}}{h_{1}}$ .

В условии сказано, что самолет пролетает над подводной лодкой, следовательно, углы α₁ и α₂ малы. Для малых углов справедливы соотношения

tg α₁ ≈ sin α₁ и tg α₂ ≈ sin α₂.

Поэтому отношение тангенсов можно заменить отношением синусов:

$\frac{\sin α_{1}}{\sin α_{2}} = \frac{h_{2}}{h_{1}}$ .

Закон преломления света, записанный в виде

n ₁ sin α₁ = n ₂ sin α₂,

позволяет получить

$\frac{\sin α_{1}}{\sin α_{2}} = \frac{n_{2}}{n_{1}}$ ,

где n ₁ — показатель преломления воздуха, n ₁ = 1; n ₂ — показатель преломления воды, n ₂ = 4/3.

Равенство левых частей записанных отношений дает

$\frac{h_{2}}{h_{1}} = \frac{n_{2}}{n_{1}}$ .

Отсюда искомая высота

$h_{2} = \frac{n_{2} h_{1}}{n_{1}}$ .

Вычислим:

$h_{2} = \frac{4 \cdot 1,5 \cdot 10^{3}}{3}$ = 2,0 ⋅ 10³ м = 2,0 км.

Кажущаяся высота полета самолета при наблюдении с подводной лодки составляет 2,0 км.

Полное внутреннее отражение от границы двух сред

Полное внутреннее отражение заключается в том, что луч света, падающий на границу раздела двух сред, не проходит во вторую среду, а распространяется вдоль границы раздела этих сред (рис. 11.7).

Рис. 11.7

Условие полного внутреннего отражения: полное внутреннее отражение может иметь место только при переходе луча света из среды с бо́льшей оптической плотностью (бо́льшим показателем преломления n ₁) в среду с меньшей оптической плотностью (меньшим показателем преломления n ₂), например из стекла в воздух и т.п.:

n ₁ > n ₂,

где n ₁ — абсолютный показатель преломления первой среды; n ₂ — абсолютный показатель преломления второй среды.

Закон полного внутреннего отражения: существует наименьший (предельный) угол падения луча на границу двух сред (см. рис. 11.7), при котором луч не переходит во вторую среду; синус этого угла определяется соотношением

$\sin α_{пр} = \frac{n_{2}}{n_{1}}$ ,

где n ₁ — абсолютный показатель преломления первой среды (из которой идет луч света); n ₂ — абсолютный показатель преломления второй среды (в которую идет луч света).

Если угол падения луча света α на границу раздела двух сред:

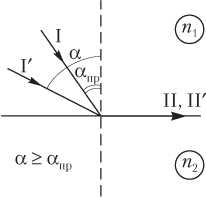
1) превышает либо равен предельному углу полного внутреннего отражения α_пр

α ≥ α_пр,

то имеет место полное внутреннее отражение, т.е. луч распространяется вдоль границы раздела двух сред (рис. 11.8);

Рис. 11.8

2) меньше предельного угла полного внутреннего отражения α_пр

α < α_пр,

то имеет место преломление луча, т.е. луч переходит в среду с меньшей оптической плотностью, отклоняясь от нормали (перпендикуляра) (рис. 11.9).

Рис. 11.9

Принцип действия оптического волокна основан на явлении полного внутреннего отражения.

Материал оптического волокна имеет больший показатель преломления, чем показатель преломления окружающей среды. Луч света, распространяясь по оптическому волокну, испытывает полное внутреннее отражение и не выходит за его пределы.

Распространение света в оптическом волокне происходит со скоростью

$v = \frac{c}{n}$ ,

где c — скорость света в вакууме, c = 3 ⋅ 10⁸ м/с; n — относительный показатель преломления материала оптического волокна.

Время распространения света по оптическому волокну определяется формулой

$t = \frac{l}{v}$ ,

где l — длина оптического волокна.

Пример 6. При переходе луча света из первой среды во вторую угол преломления равен 45°, а из первой в третью — 30° (при том же угле падения). Определить предельный угол полного внутреннего отражения для луча, идущего из третьей среды во вторую.

Решение. На рисунках изображены три ситуации:

1) луч, падая под углом i ₁ из первой среды с показателем преломления n ₁ на границу раздела первой и второй сред, преломляется (рис. а); закон преломления света имеет вид

n ₁ sin i ₁ = n ₂ sin i ₂,

где n ₂ — показатель преломления второй среды; i ₂ — угол преломления луча во второй среде;

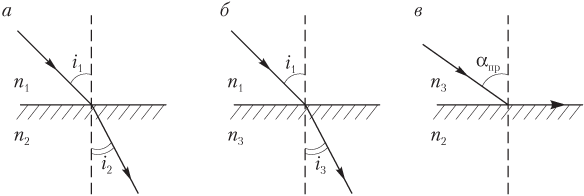
2) луч, падая под углом i ₁ из первой среды на границу раздела первой и третьей сред, преломляется (рис. б); закон преломления света имеет вид

n ₁ sin i ₁ = n ₃ sin i ₃,

где n ₃ — показатель преломления третьей среды; i ₃ — угол преломления луча в третьей среде;

3) луч, падая под углом полного внутреннего отражения α_пр из третьей среды с показателем преломления n ₃ на границу раздела третьей и второй сред, распространяется вдоль границы указанных сред (рис. в); закон полного внутреннего отражения имеет вид

$\sin α_{пр} = \frac{n_{2}}{n_{3}}$ ,

т.е. синус угла полного внутреннего отражения определяется отношением (n ₂/n ₃). Равенство левых частей двух первых уравнений позволяет найти указанное отношение:

n ₂ sin i ₂ = n ₃ sin i ₃, т.е. $\frac{n_{2}}{n_{3}} = \frac{\sin i_{3}}{\sin i_{2}}$ .

Следовательно,

$\sin α_{пр} = \frac{\sin i_{3}}{\sin i_{2}}$ .

Расчет дает значение:

$\sin α_{пр} = \frac{\sin 30 °}{\sin 45 °} = \frac{0,5}{0,5 \sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ .

Искомый угол полного внутреннего отражения составляет:

$α_{пр} = arcsin \frac{\sqrt{2}}{2} = 45 °$ .

Пример 7. Луч света распространяется в оптическом волокне длиной 225 м в течение 1,50 мкс. Оптическое волокно расположено в воздухе. Найти предельный угол полного внутреннего отражения от границы волокно — воздух.

Решение. Синус угла полного внутреннего отражения от границы волокно — воздух определяется законом полного внутреннего отражения:

$\sin α_{пр} = \frac{n_{2}}{n_{1}}$ ,

где n ₂ — показатель преломления воздуха, n ₂ = 1; n ₁ — показатель преломления волокна.

Значение показателя преломления волокна найдем из отношения

$n_{1} = \frac{c}{v}$ ,

где c — скорость света в вакууме (в воздухе), c = 3,00 ⋅ 10⁸ м/с; v — скорость распространения света в волокне.

Скорость распространения света в волокне определяется равенством

l = vt,

где l — длина оптического волокна (путь, пройденный светом), l = 225 м; t — время распространения света в волокне, t = 1,50 мкс.

Выразим отсюда скорость распространения света в волокне:

$v = \frac{l}{t}$

и подставим в выражение для показателя преломления:

$n_{1} = \frac{c t}{l}$ .

Формула для расчета синуса угла полного внутреннего отражения примет вид

$\sin α_{пр} = \frac{n_{2} l}{c t}$ .

Вычислим:

$\sin α_{пр} = \frac{1 \cdot 225}{3,00 \cdot 10^{8} \cdot 1,50 \cdot 10^{- 6}} = 0,50$ .

Следовательно, искомый угол полного внутреннего отражения от границы волокно — воздух составляет

α_пр = arcsin 0,50 = 30°.

Физика