Физика

Закон Ома для цепи переменного тока

Электромагнитные колебания в контуре с активным сопротивлением могут оставаться гармоническими при условии, что в контур включен источник электродвижущей силы (ЭДС), изменяющейся с течением времени по гармоническому закону. В этом случае говорят о переменном токе.

Переменный ток возникает в электромагнитном колебательном контуре, содержащем активное сопротивление, при подключении в контур источника ЭДС, изменяющейся с течением времени по гармоническому закону

ℰ(t) = ℰ_max cos ωt,

где ℰ_max — максимальное значение ЭДС (амплитуда ЭДС); ω — циклическая частота колебаний; t — время.

Если напряжение в цепи, содержащей последовательно включенные резистор, катушку индуктивности и конденсатор (рис. 10.18), изменяется по закону

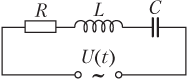
U(t) = U _max cos ωt,

то в ней течет ток, сила которого также определяется гармоническим законом

I(t) = I _max cos(ωt − φ),

где U _max — максимальное значение напряжения (амплитуда напряжения); I _max — максимальная сила тока (амплитуда силы тока); ω — циклическая частота колебаний; t — время; φ — разность фаз (сдвиг фаз) между напряжением и силой тока.

Частные случаи.

1. При подключении к цепи, содержащей резистор (рис. 10.19) переменного напряжения

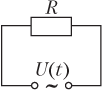
U(t) = U _max cos ωt,

сила тока через резистор определяется выражением

I(t) = I _max cos ωt,

где U _max — максимальное значение напряжения (амплитуда напряжения); I _max — максимальная сила тока (амплитуда силы тока); ω — циклическая частота колебаний; t — время.

Амплитуда силы тока определяется выражением

$I_{\text{max}}=\frac{U_{\text{max}}}{R}$,

где R — сопротивление резистора.

Сдвиг фаз между напряжением и силой тока равен нулю, т.е. на векторной диаграмме (рис. 10.20) векторы, соответствующие напряжению и силе тока, направлены одинаково.

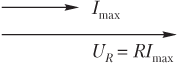
2. При подключении переменного напряжения к цепи, содержащей катушку индуктивности (рис. 10.21), падение напряжения на катушке будет изменяться со временем также по гармоническому закону

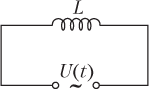
U _L (t) = U _max cos ωt,

а сила тока через катушку — определяться выражением

I(t) = I _max cos(ωt − π/2),

где U _max — максимальное значение падения напряжения на катушке (амплитуда напряжения); I _max — максимальная сила тока (амплитуда силы тока); ω — циклическая частота колебаний; t — время.

Амплитуда силы тока определяется выражением

$I_{\text{max}}=\frac{U_{\text{max}}}{R_L}$,

где R _L  — индуктивное сопротивление катушки, R _L  = ωL.

Падение напряжения на катушке опережает по фазе ток на π/2, т.е. на векторной диаграмме (рис. 10.22) векторы, соответствующие падению напряжения на катушке и силе тока в ней, отличаются на угол π/2 (угол откладывается на диаграмме против часовой стрелки).

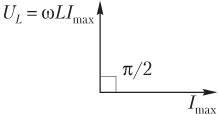
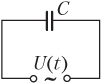
3. При подключении переменного напряжения к цепи, содержащей конденсатор (рис. 10.23), падение напряжения на обкладках конденсатора будет изменяться со временем также по гармоническому закону

U _C (t) = U _max cos ωt;

обкладки конденсатора будут постоянно перезаряжаться, т.е. в цепи потечет переменный ток, сила которого определяется выражением

I(t) = I _max cos(ωt + π/2),

где U _max — максимальное значение напряжения (амплитуда напряжения); I _max — максимальная сила тока (амплитуда силы тока); ω — циклическая частота колебаний; t — время.

Амплитуда силы тока определяется выражением

$I_{\text{max}}=\frac{U_{\text{max}}}{R_C}$,

где R _C  — емкостное сопротивление конденсатора, R _C  = 1/ωC.

Напряжение на обкладках конденсатора отстает по фазе от тока на π/2, т.е. на векторной диаграмме (рис. 10.24) векторы, соответствующие напряжению на обкладках конденсатора и силе тока в цепи, отличаются на угол π/2 (угол откладывается на диаграмме по часовой стрелке).

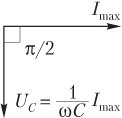
Реактивное сопротивление цепи переменному току складывается из индуктивного сопротивления и емкостного сопротивления. Однако с учетом векторных диаграмм для переменного тока в катушке индуктивности (см. рис. 10.22) и конденсаторе (см. рис. 10.24), т.е. из-за сдвига фаз между током и напряжением, формула для расчета реактивного сопротивления цепи выглядит следующим образом:

X = R _L − R _C ,

где X — реактивное сопротивление цепи; R _L  — индуктивное сопротивление катушки; R _C  — емкостное сопротивление конденсатора.

Емкостное сопротивление — сопротивление, оказываемое переменному току электрическим полем конденсатора:

$R_C=\frac{1}{\omega C}$,

где ω — циклическая частота переменного тока; C — электроемкость конденсатора.

Индуктивное сопротивление — сопротивление, оказываемое переменному току индукционным электрическим полем катушки:

R _L  = ωL,

где L — индуктивность катушки.

Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор (рис. 10.18), обладает:

• активным сопротивлением R;
• реактивным сопротивлением X;
• полным сопротивлением Z.

Закон Ома для цепи переменного тока: сила тока в цепи I равна отношению напряжения U, создаваемого в цепи генератором, к полному сопротивлению цепи переменному току Z:

$I=\frac{U}{Z}$.

Полное сопротивление цепи переменному току определяется формулой

$Z=\sqrt{R^2+X^2}=\sqrt{R^2+{(R_L-R_C)}^2}$,

где R — сопротивление резистора; R _L  — индуктивное сопротивление, R _L  = ωL; R _C  — емкостное сопротивление, R _C  = 1/ωC; ω — циклическая частота переменного тока; C — электроемкость конденсатора; L — индуктивность катушки; X — реактивное сопротивление цепи, X = R _L  − R _C .

Векторная диаграмма, представленная на рис. 10.25, наглядно иллюстрирует записанную формулу и облегчает ее запоминание.

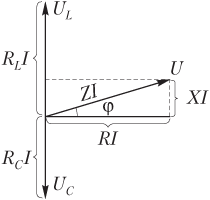
Диаграмма содержит следующие обозначения: U — напряжение, создаваемое в цепи генератором; I — сила тока; U _C  — напряжение на конденсаторе; U _L  — напряжение на катушке; U _R  — напряжение на резисторе.

В цепи переменного тока, содержащей последовательно включенные резистор, катушку индуктивности и конденсатор (см. рис. 10.18), между напряжением

U(t) = U _max cos ωt

и силой тока

I(t) = I _max cos(ωt − φ)

существует сдвиг фаз φ, тангенс которого определяется формулой

$\mathrm{tg}\phi =\frac{X}{R}=\frac{R_L-R_C}{R}$,

где R — сопротивление резистора; X — реактивное сопротивление цепи, X = R _L  − R _C ; R _L  — индуктивное сопротивление, R _L  = ωL; R _C  — емкостное сопротивление, R _C  = 1/ωC.

Векторная диаграмма (см. рис. 10.25) иллюстрирует формулу для расчета сдвига фаз между силой тока и напряжением.

Тепловое действие переменного тока

Мгновенное значение мощности переменного тока — произведение мгновенных значений силы тока и напряжения в цепи:

P(t) = I(t)U(t),

где I(t) — мгновенное значение силы тока; U(t) — мгновенное значение напряжения.

Практическое значение имеет среднее значение мощности переменного тока, которое определяется формулой

$\langle P\rangle =\frac{1}{2}{I}_{\text{max}}{U}_{\text{max}}\cos \phi$,

где I _max — максимальное значение силы тока; U _max — максимальное значение напряжения; φ — сдвиг фаз между током и напряжением; cos φ — коэффициент мощности.

Коэффициент мощности показывает, какая часть электрической энергии переходит в другие виды энергии, и определяется сдвигом фаз φ между током и напряжением; наиболее удобным для расчета коэффициента мощности является выражение

$\cos \phi =\frac{R}{Z}=\frac{R}{\sqrt{R^2+{(R_L-R_C)}^2}}$,

где Z — полное сопротивление цепи; R — сопротивление резистора; R _L  — индуктивное сопротивление, R _L  = ωL; R _C  — емкостное сопротивление, R _C  = 1/ωC.

Формула для расчета тангенса сдвига фаз φ между током и напряжением имеет следующий вид:

$\mathrm{tg}\phi =\frac{X}{R}=\frac{R_L-R_C}{R}$.

Коэффициент мощности отличен от нуля только при наличии в цепи активного сопротивления:

1) если активное сопротивление в цепи отсутствует (R = 0), то коэффициент мощности имеет минимальное значение, равное нулю: cos φ = 0;

2) если реактивное сопротивление в цепи отсутствует (X = R _L  − R _C  = = 0), то коэффициент мощности максимален и равен единице: cos φ = 1.

Действующие (эффективные) значения силы тока и напряжения — значения силы и напряжения постоянного тока, при протекании которого по данной цепи выделяется такое же количество теплоты, как и при протекании переменного тока, — определяются из формулы

$\langle P\rangle =I_{\text{д}}{U}_{\text{д}}\cos \phi$,

где I _д — действующее значение силы переменного тока; U _д — действующее значение напряжения переменного тока; cos φ — коэффициент мощности цепи переменного тока.

Действующие значения рассчитываются по следующим формулам:

• силы переменного тока —

$I_{\text{д}}=\frac{I_{\text{max}}}{\sqrt{2}}$;

• напряжения переменного тока —

$U_{\text{д}}=\frac{U_{\text{max}}}{\sqrt{2}}$,

где I _max — максимальное значение силы переменного тока; U _max — максимальное значение напряжения переменного тока.

Приборы для измерения силы тока (амперметры) и напряжения (вольтметры) градуируются по действующим значениям силы тока и напряжения.

Средняя мощность переменного тока показывает, сколько энергии за единицу времени безвозвратно передается электрическим током данному участку цепи.

В цепи переменного тока энергию потребляет только активное сопротивление, поэтому среднюю мощность называют также активной:

$\langle P\rangle =P_{\text{акт}}=I_{\text{д}}{U}_{\text{д}}\cos \phi =I_{\text{д}}^{2}R$,

где I _д — действующее значение силы переменного тока; U _д — действующее значение переменного напряжения; cos φ — коэффициент мощности цепи переменного тока; R — активное сопротивление цепи (сопротивление резистора).

Произведение действующих значений силы переменного тока и напряжения называют кажущейся мощностью:

$P_{\text{каж}}=I_{\text{д}}{U}_{\text{д}}=\frac{P_{\text{акт}}}{\cos \phi }$,

где P _акт — активная мощность, P _акт = I _дU _д cos φ; cos φ — коэффициент мощности цепи переменного тока.

Прибор для измерения мощности (ваттметр) градуируется по средней (активной) мощности.

Теплота в цепи переменного тока выделяется только на резисторе, т.е. только на активном сопротивлении; на индуктивном и емкостном сопротивлении теплота не выделяется.

Количество теплоты, выделяющейся на резисторе, включенном в цепь переменного тока, определяется законом Джоуля — Ленца, однако форма записи данного закона зависит от наличия в цепи реактивного сопротивления:

• при наличии в цепи реактивного сопротивления —

$Q=I_{\text{д}}^{2}Rt$,

где I _д — действующее значение силы переменного тока; R — активное сопротивление цепи (сопротивление резистора); t — время;

• при отсутствии в цепи реактивного сопротивления —

$Q=I_{\text{д}}{U}_{\text{д}}t=\frac{U_{\text{д}}^2}{R}t$,

где I _д — действующее значение силы переменного тока; U _д — действующее значение переменного напряжения; t — время; R — активное сопротивление цепи (сопротивление резистора).