Физика

Механические волны представляют собой процесс распространения механических колебаний в упругой среде. При этом каждая точка среды совершает колебания около своего положения равновесия.

Точки среды не перемещаются в направлении распространения волны; в направлении распространения волны происходит лишь перенос энергии (без переноса вещества).

Упругие волны бывают продольными и поперечными. Частицы среды колеблются относительно своих положений равновесия:

• в продольных волнах — в направлении распространения волны;
• в поперечных волнах — в плоскостях, перпендикулярных направлению распространения волны.

В газах могут распространяться только продольные волны, в конденсированных средах (жидкостях и твердых телах) — как продольные, так и поперечные.

Упругая волна является гармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Смещение конкретной точки среды от положения равновесия изменяется с течением времени по закону

x(t) = A cos ωt,

где A — максимальное отклонение точки от положения равновесия (амплитуда колебаний); ω — циклическая частота колебаний; t — время.

График колебаний — зависимость смещения выбранной точки среды (от положения равновесия) от времени (рис. 10.26).

Смещение всех точек среды, лежащих на оси Ox, от своего положения равновесия при распространении поперечной волны в положительном направлении указанной оси описывается уравнением

y(x, t) = A cos(ωt − kx),

где x — координата конкретной точки волны в момент времени t; A — максимальное отклонение точки от положения равновесия (амплитуда волны); ω — циклическая частота колебаний; k — волновое число, k = 2π/λ; λ — длина волны; (ωt − kx) — фаза.

График волны — зависимость смещения всех частиц среды (от положения равновесия) от их координаты в фиксированный момент времени (рис. 10.27); координата точки определяет ее расстояние от источника колебаний S.

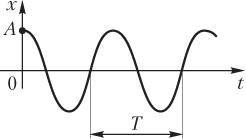
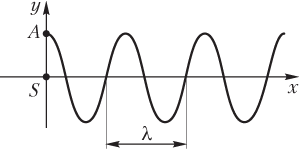
График волны, по сути, представляет собой моментальную фотографию, фиксирующую отклонение всех точек среды от своего положения равновесия в один и тот же момент времени.

Длина волны связана со скоростью ее распространения v и некоторыми характеристиками колебаний точек среды следующими формулами:

• с периодом колебаний T —

λ = vT,

где v — модуль скорости распространения волны; T — период колебаний;

• частотой ν —

$\lambda =\frac{v}{\nu }$,

где ν — частота колебаний;

• циклической частотой ω —

$\lambda =\frac{2\pi v}{\omega }$,

где ω — циклическая частота колебаний.

В Международной системе единиц длина волны измеряется в метрах (1 м).

Две точки среды, имеющие разные координаты и находящиеся на оси, вдоль которой распространяется волна, обладают различной фазой колебаний.

Сдвиг фаз для двух точек одной волны, находящихся на разном расстоянии от источника колебаний, определяется формулой

$\Delta \phi =\frac{2\pi }{\lambda }\left|x_1-x_2\right|$,

где λ — длина волны; x ₁ — координата первой точки; x ₂ — координата второй точки.

Если две соседние точки одной волны совершают колебания:

• в одинаковой фазе, или синфазно (Δφ = 2π), то расстояние между ними равно длине волны:

$\Delta x=\left|x_1-x_2\right|=\lambda$;

• противоположной фазе, или в противофазе (Δφ = π), то расстояние между ними равно половине длины волны:

$\Delta x=\left|x_1-x_2\right|=\frac{\lambda }{2}$.

В Международной системе единиц сдвиг фаз измеряется в радианах (1 рад).

Смещение точек среды, имеющих разные координаты, от положения равновесия в зависимости от времени определяется следующими уравнениями (уравнениями волны):

• при распространении упругой поперечной волны в положительном направлении оси Ox —

y(x, t) = A sin(ωt − kx);

• распространении упругой поперечной волны в отрицательном направлении оси Ox —

y(x, t) = A sin(ωt + kx),

где A — максимальное отклонение точки от положения равновесия (амплитуда волны); ω — циклическая частота; t — время; x — координата конкретной точки волны; k — волновое число, k = 2π/λ; λ — длина волны.

Записанные уравнения описывают бегущую волну, т.е. волну, переносящую энергию в определенном направлении.

При наложении двух бегущих в противоположных направлениях волн одинаковой частоты и амплитуды образуется стоячая волна (рис. 10.28), описываемая уравнением

$y(x,t)=2A\sin \frac{2\pi x}{\lambda }\sin \omega t$,

где 2A sin 2πx/λ — амплитуда стоячей волны.

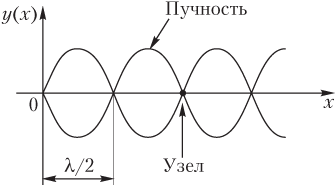
Амплитуда стоячей волны зависит от координаты точки (ее расстояния от источника колебаний) и является для данной точки постоянной (не зависящей от времени) величиной:

• точки с максимальной амплитудой колебаний называются пучностями;
• точки с нулевой амплитудой колебаний называются узлами (точки среды, находящиеся в узлах, покоятся).

Расстояние между узлами равно расстоянию между пучностями и равно половине длины волны:

$\Delta x=\frac{\lambda }{2}$.