Репетитор-онлайн — подготовка к ЦТ

10.2. Основные характеристики колебаний

10.2.2. Влияние внешних условий на основные характеристики механических колебаний

На характеристики колебательного процесса (период, частоту, циклическую частоту) оказывают влияние следующие факторы: величина ускорения свободного падения в месте расположения колебательной системы, наличие внешних полей, а также наличие ускорения у самой колебательной системы.

При перемещении маятника с земной поверхности на поверхность другой планеты изменяется ускорение свободного падения и, следовательно, изменяются характеристики колебательного процесса.

Модуль ускорения свободного падения (в отсутствие внешних полей) определяется следующими формулами:

для поверхности Земли —

$g_{0} = \frac{G M_{0}}{R_{0}^{2}}$ ,

где G — универсальная гравитационная постоянная, G = 6,67 ⋅ 10⁻¹¹ м³/(кг ⋅ с²); M ₀ — масса Земли; R ₀ — радиус Земли; при решении задач рекомендуется пользоваться значением g ₀ = 10 м/с²;

для поверхности другой планеты —

${g^{'}}_{0} = \frac{G M}{R^{2}}$ ,

где M — масса планеты; R — радиус планеты.

При поднятии маятника с поверхности планеты на некоторую высоту также изменяется ускорение свободного падения и, следовательно, изменяются характеристики колебательного процесса.

Модуль ускорения свободного падения (в отсутствие внешних полей) определяется следующими формулами:

на некоторой высоте над поверхностью Земли —

$g = \frac{G M_{0}}{{(R_{0} + h)}^{2}}$ ,

где G — универсальная гравитационная постоянная, G = 6,67 ⋅ 10⁻¹¹ м³/(кг ⋅ с²); M ₀ — масса Земли; R ₀ — радиус Земли; h — высота над поверхностью Земли;

на некоторой высоте над поверхностью другой планеты —

$g^{'} = \frac{G M}{{(R + h)}^{2}}$ ,

где M — масса планеты; R — радиус планеты; h — высота над поверхностью планеты.

При использовании формул для расчета модуля ускорения свободного падения на поверхности планеты (в том числе и Земли)

$g_{0} = \frac{G M}{R^{2}}$

и на некоторой высоте над поверхностью планеты

$g = \frac{G M}{{(R + h)}^{2}}$ ,

где G — универсальная гравитационная постоянная, G = 6,67 ⋅ 10⁻¹¹ м³/(кг ⋅ с²); M — масса планеты; R — радиус планеты; h — высота над поверхностью планеты,

могут возникнуть затруднения из-за отсутствия в условии значений массы и радиуса планеты.

Указанные трудности устраняются, если воспользоваться:

числовым значением ускорения свободного падения на поверхности Земли, т.е. значением выражения

$g_{0} = \frac{G M_{0}}{R_{0}^{2}} = 10$ м/с²,

где M ₀ — масса Земли; R ₀ — радиус Земли;

приближением, что планета представляет собой шар плотностью ρ и радиусом R и ее масса есть произведение:

$M = ρ V_{шара} = \frac{4}{3} π ρ R^{3}$ .

Если маятник находится в некотором объекте (лифт, ракета, автомобиль и т.п.), движущемся с ускорением, то при расчете характеристик колебательного процесса относительно неинерциальной системы отсчета (НИСО), связанной с данным объектом, в соответствующих формулах следует заменить ускорение свободного падения на его эффективное значение:

${\vec{g}}_{эфф} = {\vec{g}}_{0} + \vec{a}$ ,

где ${\vec{g}}_{0}$ — ускорение свободного падения на поверхности Земли, g ₀ = 10 м/с²; $\vec{a}$ — ускорение, вызванное силой инерции, $\vec{a} = {\vec{F}}_{i} / m$ ; ${\vec{F}}_{i}$ — сила инерции, действующая на груз маятника, ${\vec{F}}_{i} = - m {\vec{a}}^{*}$ ; m — масса груза маятника; ${\vec{a}}^{*}$ — ускорение НИСО.

В неинерциальных системах отсчета:

векторы ${\vec{g}}_{0}$ и $\vec{a}$ направлены в одну сторону, если ускорение НИСО ${\vec{a}}^{*}$ направлено вверх (например, маятник находится в ракете, стартующей вверх); эффективное значение ускорения представляет собой сумму (рис. 10.3):

Рис. 10.3

Рис. 10.4

Рис. 10.5

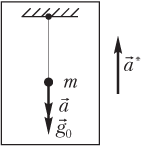
g _эфф = g ₀ + a;

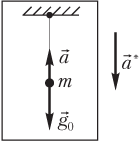
векторы ${\vec{g}}_{0}$ и $\vec{a}$ направлены в противоположные стороны, если ускорение НИСО ${\vec{a}}^{*}$ направлено вниз (например, маятник находится в лифте, ускорение которого направлено вниз); эффективное значение ускорения представляет собой разность (рис. 10.4):

g _эфф = g ₀ − a;

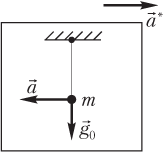
вектор ${\vec{g}}_{0}$ направлен вертикально вниз, а вектор $\vec{a}$ — горизонтально, если ускорение НИСО ${\vec{a}}^{*}$ направлено горизонтально (например, маятник находится в вагоне, ускорение которого направлено горизонтально); эффективное значение ускорения рассчитывается по теореме Пифагора (рис. 10.5):

$g_{эфф} = \sqrt{g_{0}^{2} + a^{2}}$ .

Если груз маятника обладает зарядом и находится в электростатическом поле, то в формулах, определяющих характеристики колебательного процесса, следует заменить ускорение свободного падения на его эффективное значение:

${\vec{g}}_{эфф} = {\vec{g}}_{0} + \vec{a}$ ,

где ${\vec{g}}_{0}$ — ускорение свободного падения на поверхности Земли, g ₀ = 10 м/с²; $\vec{a}$ — ускорение, вызванное силой кулоновского взаимодействия заряда и поля, $\vec{a} = \vec{F} / m$ ; $\vec{F}$ — сила, действующая на груз маятника со стороны поля, $\vec{F} = q \vec{E}$ ; m — масса груза маятника; q — его заряд; $\vec{E}$ — напряженность электростатического поля.

В электростатическом поле:

векторы ${\vec{g}}_{0}$ и $\vec{a}$ направлены в одну сторону, если груз маятника обладает положительным зарядом, а силовые линии поля направлены вниз (рис. 10.6, а); эффективное значение ускорения представляет собой сумму:

g _эфф = g ₀ + a;

Рис. 10.6

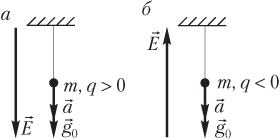
векторы ${\vec{g}}_{0}$ и $\vec{a}$ направлены в противоположные стороны, если груз маятника обладает положительным зарядом, а силовые линии поля направлены вверх (рис. 10.7, а); эффективное значение ускорения представляет собой разность:

Рис. 10.7

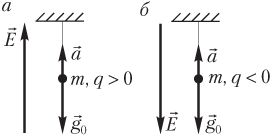
g _эфф = g ₀ − a;

вектор ${\vec{g}}_{0}$ направлен вертикально вниз, а вектор $\vec{a}$ — горизонтально, если груз маятника обладает положительным зарядом, а силовые линии поля направлены горизонтально (рис. 10.8, а); эффективное значение ускорения рассчитывается по теореме Пифагора:

Рис. 10.8

$g_{эфф} = \sqrt{g_{0}^{2} + a^{2}}$ .

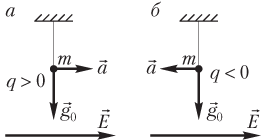
Для отрицательного заряда ускорение $\vec{a}$ направлено в сторону, противоположную силовым линиям поля $\vec{E}$ (рис. 10.6–10.8, б).

Если пружинный маятник составлен из нескольких пружин, соединенных между собой различными способами, то в формулах, определяющих характеристики колебательного процесса, следует заменить коэффициент жесткости (упругости) пружины на его эффективное значение, рассчитанное по формулам:

для параллельного соединения пружин —

k _эфф = k ₁ + k ₂ + ... + k _n;

для последовательного соединения пружин —

$\frac{1}{k_{эфф}} = \frac{1}{k_{1}} + \frac{1}{k_{2}} + ... + \frac{1}{k_{n}}$ ,

где k ₁ — коэффициент жесткости первой пружины; k ₂ — коэффициент жесткости второй пружины; ...; k _n — коэффициент жесткости n-й пружины.

Пример 2. Период колебаний некоторого математического маятника на поверхности Земли равен 4,8 с. Маятник переносят на поверхность планеты, радиус которой в 1,8 раза превышает радиус Земли, а плотность в 3,6 раза меньше плотности Земли. Определить период колебаний данного маятника на поверхности планеты.

Решение. При перемещении маятника с земной поверхности на поверхность другой планеты изменяется ускорение свободного падения и, следовательно, период его колебаний.

Период колебаний математического маятника определяется следующими формулами:

на поверхности Земли —

$T_{0} = 2 π \sqrt{\frac{l}{g_{0}}}$ ,

где l — длина нити маятника; g ₀ — модуль ускорения свободного падения на поверхности Земли;

на поверхности планеты —

$T = 2 π \sqrt{\frac{l}{g}}$ ,

где g — модуль ускорения свободного падения на поверхности планеты.

Отношение уравнений

$\frac{T_{0}}{T} = \sqrt{\frac{g}{g_{0}}}$

позволяет выразить искомый период математического маятника на поверхности планеты:

$T = T_{0} \sqrt{\frac{g_{0}}{g}}$ .

Чтобы определить период, необходимо найти отношение модулей ускорения свободного падения. Для этого запишем следующие формулы, определяющие модуль ускорения свободного падения:

для поверхности Земли —

$g_{0} = \frac{G M_{0}}{R_{0}^{2}}$ ,

где G — универсальная гравитационная постоянная, G = 6,67 ⋅ 10⁻¹¹ м³/(кг ⋅ с²); M ₀ — масса Земли; R ₀ — радиус Земли;

для поверхности планеты —

$g = \frac{G M}{R^{2}}$ ,

где M — масса планеты; R — радиус планеты.

Их отношение

$\frac{g}{g_{0}} = \frac{M R_{0}^{2}}{M_{0} R^{2}}$

определяется отношением масс и радиусов.

Считая, что Земля и планета имеют форму шара, запишем для их масс следующие выражения:

масса Земли —

$M_{0} = \frac{4}{3} π ρ_{0} R_{0}^{3}$ ,

где ρ₀ — плотность Земли;

масса планеты —

$M = \frac{4}{3} π ρ R^{3}$ ,

где ρ — плотность планеты.

Отношение масс составляет

$\frac{M}{M_{0}} = \frac{ρ R^{3}}{ρ_{0} R_{0}^{3}}$ ,

а отношение модулей ускорения свободного падения —

$\frac{g}{g_{0}} = \frac{ρ R^{3} R_{0}^{2}}{ρ_{0} R_{0}^{3} R^{2}} = \frac{ρ R}{ρ_{0} R_{0}}$ ,

или с учетом R = 1,8R ₀ и ρ₀ = 3,6ρ —

$\frac{g}{g_{0}} = \frac{1,8 R_{0} ρ}{3,6 ρ R_{0}} = \frac{1}{2}$ .

Подставим полученное отношение в формулу для вычисления искомого периода математического маятника на поверхности планеты:

$T = T_{0} \sqrt{\frac{g_{0}}{g}} = T_{0} \sqrt{2}$ ,

где T ₀ — период колебаний этого маятника на поверхности Земли, T ₀ = 4,8 c.

Расчет дает значение:

$T = 4,8 \cdot \sqrt{2} = 6,8$ с.

Пример 3. Математический маятник поместили в ракету, стартующую с поверхности Земли с ускорением 12 м/с². Нить маятника имеет длину 20 см. Считая ускорение свободного падения постоянным и равным ускорению свободного падения на поверхности Земли, определить период колебаний маятника в ракете.

Решение. Если маятник находится в ракете, стартующей с поверхности Земли с ускорением, направленным вверх, то в формуле для периода колебаний следует заменить модуль ускорения свободного падения g ₀ его эффективным значением:

g _эфф = g ₀ + a,

где g ₀ — модуль ускорения свободного падения на поверхности Земли, g ₀ = 10 м/с²; a — модуль ускорения ракеты, a = 12 м/с².

Следовательно, период колебаний математического маятника в ракете определяется следующей формулой:

$T = 2 π \sqrt{\frac{l}{g_{эфф}}} = 2 π \sqrt{\frac{l}{g_{0} + a}}$ ,

где l — длина нити маятника, l = 20 см.

Вычислим:

$T = 2 \cdot 3,14 \sqrt{\frac{20 \cdot 10^{- 2}}{10 + 12}} = 0,60$ c.

Период колебаний маятника в ракете составляет 0,60 с.

Пример 4. Определить период колебаний математического маятника с длиной нити 60 см, находящегося в самолете, движущемся горизонтально с ускорением 10 м/с².

Решение. На рисунке показаны следующие векторы:

вектор ускорения свободного падения ${\vec{g}}_{0}$ , направленный вниз;
вектор ускорения $\vec{a}$ , направленный горизонтально (вправо); его появление вызвано силой инерции, действующей на маятник в самолете (ускорение самолета направлено влево);
результирующий вектор

${\vec{g}}_{эфф} = {\vec{g}}_{0} + \vec{a}$ .

Для маятника, находящегося в самолете, движущемся с горизонтальным ускорением, в формуле для периода колебаний следует заменить ускорение свободного падения g ₀ его эффективным значением:

$g_{эфф} = \sqrt{g_{0}^{2} + a^{2}}$ ,

где g ₀ — модуль ускорения свободного падения на поверхности Земли, g ₀ = 10 м/с²; a — модуль ускорения самолета, a = 10 м/с².

Следовательно, период колебаний математического маятника, находящегося в самолете, определяется формулой

$T = 2 π \sqrt{\frac{l}{g_{эфф}}} = 2 π \sqrt{\frac{l}{\sqrt{g_{0}^{2} + a^{2}}}}$ ,

где l — длина нити маятника, l = 60 см.

Вычислим:

$T = 2 \cdot 3,14 \sqrt{\frac{60 \cdot 10^{- 2}}{\sqrt{10^{2} + 10^{2}}}} = 1,3$ c.

Период колебаний маятника в самолете составляет 1,3 с.

Пример 5. Шарик математического маятника обладает массой 0,30 кг и зарядом −50 мкКл. Во сколько раз возрастет период колебаний математического маятника, если его поместить в вертикальное однородное электрическое поле с напряженностью 45 кВ/м?

Решение. Если груз маятника обладает зарядом, а маятник находится в электростатическом поле, то в формуле, определяющей период его колебаний, следует заменить ускорение свободного падения на эффективное значение:

${\vec{g}}_{эфф} = {\vec{g}}_{0} + \vec{a}$ ,

где ${\vec{g}}_{0}$ — ускорение свободного падения на поверхности Земли; $\vec{a}$ — ускорение, вызванное силой кулоновского взаимодействия заряда и поля, $\vec{a} = {\vec{F}}_{кул} / m$ ; ${\vec{F}}_{кул}$ — сила, действующая на шарик маятника со стороны поля, ${\vec{F}}_{кул} = q \vec{E}$ ; m — масса шарика; q — его заряд; $\vec{E}$ — напряженность электростатического поля.

Период колебаний математического маятника определяется следующими формулами:

в отсутствие электростатического поля —

$T_{0} = 2 π \sqrt{\frac{l}{g_{0}}}$ ,

где l — длина нити маятника; g ₀ — модуль ускорения свободного падения, g ₀ = 10 м/с²;

в вертикальном электростатическом поле —

$T = 2 π \sqrt{\frac{l}{g_{эфф}}} = 2 π \sqrt{\frac{l}{g_{0} \pm a}}$ ,

где a — модуль ускорения, вызванного наличием поля, a = |q|E/m; |q| — модуль заряда шарика маятника, |q| = 50 мкКл; m — масса шарика, m = 0,30 кг; E — модуль напряженности электростатического поля, E = 45 кВ/м.

По условию задачи период колебаний возрастает; следовательно, g _эфф должно быть меньше ускорения свободного падения g ₀ на поверхности Земли. Поэтому g _эфф определяется разностью:

g _эфф = g ₀ − a,

а формула для периода колебаний маятника в электростатическом поле принимает вид

$T = 2 π \sqrt{\frac{l}{g_{0} - a}}$ .

На рисунке показаны силы, действующие на шарик маятника в электростатическом поле. Сила тяжести $m {\vec{g}}_{0}$ и сила Кулона ${\vec{F}}_{кул}$ направлены в разные стороны, так как векторы ${\vec{g}}_{0}$ и $\vec{a}$ имеют противоположные направления. Шарик заряжен отрицательно, поэтому вектор напряженности электростатического поля $\vec{E}$ направлен в сторону, противоположную кулоновской силе ${\vec{F}}_{кул}$ , т.е. вниз.

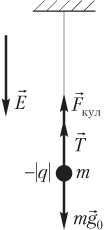
Искомое отношение периодов определяется формулой

$\frac{T}{T_{0}} = \sqrt{\frac{g_{0}}{g_{0} - a}} = \sqrt{\frac{g_{0}}{g_{0} - \frac{| q | E}{m}}}$ .

Вычислим:

$\frac{T}{T_{0}} = \sqrt{\frac{10}{10 - \frac{| - 50 \cdot 10^{- 6} | \cdot 45 \cdot 10^{3}}{0,30}}} = 2,0$ .

При включении электростатического поля, силовые линии которого направлены вниз, период колебаний маятника увеличивается в 2,0 раза.

Физика