Репетитор-онлайн — подготовка к ЦТ

9.4. Явление электромагнитной индукции

9.4.4. Мгновенные значения электродвижущей силы электромагнитной индукции и самоиндукции

Модуль мгновенного значения ЭДС электромагнитной индукции в указанный момент времени рассчитывают по формуле

|ℰ_i| = |Φ′(t)|,

где Ф′(t) — производная функции магнитного потока по времени.

Модуль мгновенного значения ЭДС самоиндукции в указанный момент времени рассчитывают по формуле

|ℰ_si| = |Φ′_s(t)|,

где Φ′_s(t) — производная функции магнитного потока, сцепленного с контуром, по времени.

Мгновенное значение ЭДС электромагнитной индукции может быть рассчитано графически как тангенс угла наклона графика функции Ф(t) к оси времени (рис. 9.22):

$|ℰ_{i}| = tg α$ ,

где tg α — скорость изменения магнитного потока с течением времени, tg α = |∆Ф|/∆t; α — угол наклона графика Ф(t) к положительному направлению оси времени.

Рис. 9.22

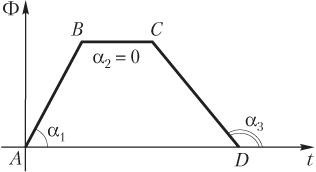
Следует заметить, что ЭДС электромагнитной индукции:

при возрастании магнитного потока с течением времени (угол наклона α₁ к положительному направлению оси времени — острый) имеет отрицательный знак (участок AB);
неизменном значении магнитного потока (угол наклона α₂ к положительному направлению оси времени — нулевой) не возникает (участок BC);
убывании магнитного потока с течением времени (угол наклона α₃ к положительному направлению оси времени — тупой) имеет положительный знак (участок CD).

Аналогично рассчитывается мгновенное значение ЭДС электромагнитной индукции с помощью следующих графических зависимостей:

1) по графику B _x(t) —

$| ℰ_{i} | = S tg α$ ,

где S — площадь, ограниченная контуром; tg α = ΔB _x/Δt;

2) по графику S(t) —

$| ℰ_{i} | = B_{x} tg α$ ,

где В _x — проекция вектора магнитной индукции на нормаль (перпендикуляр) к плоскости контура; tg α = ΔS/Δt.

Мгновенное значение ЭДС самоиндукции может быть определено графически как тангенс угла наклона графика функции Ф_s(t) к оси времени (рис. 9.23):

$| ℰ_{i s} | = tg β$ ,

где tg β — скорость изменения магнитного потока, сцепленного с контуром, с течением времени, tg β = |∆Ф_s|/∆t; β — угол наклона графика Ф_s(t) к положительному направлению оси времени.

Рис. 9.23

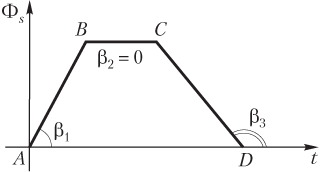
Следует заметить, что ЭДС самоиндукции:

при возрастании магнитного потока, сцепленного с контуром, с течением времени (угол наклона β₁ к положительному направлению оси времени — острый) имеет отрицательный знак (участок AB);
неизменном значении магнитного потока, сцепленного с контуром (угол наклона β₂ к положительному направлению оси времени — нулевой), не возникает (участок BC);
убывании магнитного потока, сцепленного с контуром, с течением времени (угол наклона β₃ к положительному направлению оси времени — тупой) имеет положительный знак (участок CD).

Аналогично рассчитывается мгновенное значение ЭДС самоиндукции с помощью следующих графических зависимостей:

1) по графику I(t) —

$| ℰ_{i s} | = L tg β$ ,

где L — индуктивность контура; tg β = ΔI/Δt;

2) по графику L(t) —

$| ℰ_{i s} | = I tg β$ ,

где I — сила тока в контуре; tg β =ΔL/Δt.

Пример 17. График зависимости величины индукции магнитного поля от времени B(t) показан на рисунке. В данное поле поместили замкнутый проводящий контур в виде квадрата со стороной 20,0 см таким образом, что его плоскость перпендикулярна силовым линиям поля. Определить мгновенное значение ЭДС индукции в контуре в начале шестой секунды.

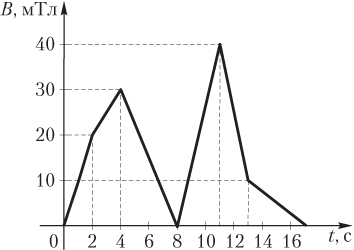
Решение. Мгновенное значение ЭДС индукции в указанный момент t = 5 c совпадает с ее средним значением в интервале времени от t ₁ = 4 с до t ₂ = 8 с, так как величина индукции магнитного поля в указанном интервале уменьшается равномерно от B ₁ = 30 мТл до B ₂ = 0:

$ℰ_{i} (5 с) = 〈 ℰ_{i} 〉$ .

Среднее значение ЭДС индукции, возникающей в контуре при изменении индукции магнитного поля:

$〈 ℰ_{i} 〉 = | \frac{Δ Ф}{Δ t} | = | \frac{(B_{2} - B_{1}) S \cos α}{Δ t} |$ ,

где S — площадь квадрата, S = a ²; a — сторона квадрата, a = 20,0 см; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата, α = 0°; ∆t — интервал времени, ∆t = t ₂ − t ₁.

С учетом выражения для площади квадрата и значения угла α получим формулу для искомой величины:

$ℰ_{i} (5 с) = | \frac{(B_{2} - B_{1}) a^{2}}{Δ t} |$ .

Рассчитаем:

$ℰ_{i} (5 с) = | \frac{(0 - 30 \cdot 10^{- 3}) {(20,0 \cdot 10^{- 2})}^{2}}{8 - 4} | = 0,30 \cdot 10^{- 3} = 0,30$ мВ.

Мгновенное значение ЭДС индукции в начале шестой секунды составляет 300 мкВ.

Пример 18. График зависимости силы тока в замкнутом контуре от времени I(t) показан на рисунке. Определить модуль ЭДС самоиндукции, которая возникнет в контуре в конце третьей секунды, если индуктивность контура равна 20 мГн.

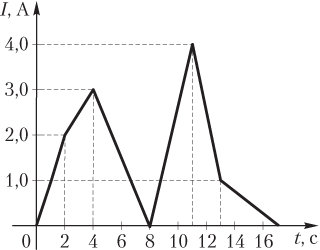
Решение. Мгновенное значение ЭДС самоиндукции в указанный момент t = 3 c совпадает с ее средним значением в интервале времени от t ₁ = 2 с до t ₂ = 4 с, так как сила тока в указанном интервале возрастает равномерно от I ₁ = 2,0 А до I ₂ = 3,0 А: $ℰ_{s i} (3 с) = 〈 ℰ_{s i} 〉$ .

Среднее значение ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем:

$〈 ℰ_{s i} 〉 = | \frac{Δ Ф_{s}}{Δ t} | = | \frac{L (I_{2} - I_{1})}{Δ t} |$ ,

где L — индуктивность контура, L = 20 мГн; ∆t — интервал времени, ∆t = t ₂ − t ₁.

Искомая величина также определяется полученной формулой:

$ℰ_{s i} (3 с) = | \frac{L (I_{2} - I_{1})}{Δ t} |$ .

Расчет дает:

$ℰ_{s i} (3 с) = | \frac{20 \cdot 10^{- 3} (3,0 - 2,0)}{4 - 2} | = 10 \cdot 10^{- 3} В = 10$ мВ.

Мгновенное значение ЭДС самоиндукции в конце третьей секунды составляет 10 мВ.

Пример 19. Сила тока, протекающего в замкнутом проводящем контуре, изменяется по закону I(t) = (25 + 150t), где сила тока задана в амперах, время — в секундах. Индуктивность контура составляет 0,20 мГн. Определить мгновенное значение ЭДС самоиндукции, возникающей в контуре, в конце семнадцатой секунды.

Решение. Поток самоиндукции, сцепленный с контуром, зависит от времени:

$Ф_{s} (t) = L I (t) = L (25 + 150 t)$ ,

где L — индуктивность контура, L = 0,20 мГн; I — сила тока, I(t) = = (25 + 150t); t — время.

Модуль мгновенного значения ЭДС электромагнитной самоиндукции в указанный момент рассчитывают по формуле

|ℰ_si| = |Φ′_s(t)|,

где Φ′_s(t) — производная функции магнитного потока, сцепленного с контуром, по времени, Φ′_s(t) = 150L.

Следует отметить, что при линейной зависимости силы тока от времени производная Φ′_s(t) (а значит, и ЭДС самоиндукции) является постоянной величиной, т.е. не зависит от времени. Поэтому величина ЭДС самоиндукции в любой момент времени, в том числе t = 17 с, определяется формулой

$| ℰ_{s i} | = 150 L$ .

Рассчитаем:

$| ℰ_{s i} | = 150 \cdot 0,20 \cdot 10^{- 3} = 30 \cdot 10^{- 3} В = 30$ мВ.

Физика