Репетитор-онлайн — подготовка к ЦТ

9.4. Явление электромагнитной индукции

9.4.2. Среднее значение электродвижущей силы электромагнитной индукции

При изменении потока вектора индукции магнитного поля через площадь, ограниченную замкнутым проводящим контуром, в нем появляется вихревое электрическое поле и течет индукционный ток — явление электромагнитной индукции.

Модуль средней электродвижущей силы ( ЭДС) индукции за определенный промежуток времени рассчитывают по формуле

$〈 | ℰ_{i} | 〉 = \frac{| Δ Ф |}{Δ t}$ ,

где ΔФ — изменение магнитного потока за время Δt.

Если магнитное поле изменяется с течением времени B = B(t), то:

изменение потока определяется формулой

∆Ф = ∆BS cos α,

где ΔB — изменение индукции магнитного поля за время Δt; S — площадь, ограниченная контуром; α — угол между нормалью (перпендикуляром) к площадке и вектором $\vec{B}$ ;

модуль средней ЭДС индукции рассчитывается с помощью выражения

$〈 | ℰ_{i} | 〉 = \frac{| Δ B |}{Δ t} S \cos α$ ,

где ΔB/Δt — скорость изменения модуля индукции магнитного поля.

Если площадь контура изменяется с течением времени S = S(t), то:

изменение потока определяется формулой

∆Ф = B∆S cos α,

где B — модуль индукции магнитного поля; ΔS — изменение площади, ограниченной контуром, за время Δt; α — угол между нормалью (перпендикуляром) к площадке и вектором $\vec{B}$ ;

модуль средней ЭДС индукции рассчитывается с помощью выражения

$〈 | ℰ_{i} | 〉 = B \frac{| Δ S |}{Δ t} \cos α$ .

Если ориентация контура в магнитном поле изменяется с течением времени α = α(t), то:

изменение потока определяется формулой

∆Ф = BS(cos α₂ − cos α₁),

где B — модуль индукции магнитного поля; S — площадь, ограниченная контуром; α₁ — угол между нормалью (перпендикуляром) к площадке и вектором $\vec{B}$ в начальный момент времени; α₂ — угол между нормалью (перпендикуляром) к площадке и вектором $\vec{B}$ через промежуток времени Δt;

модуль средней ЭДС индукции рассчитывается с помощью выражения

$〈 | ℰ_{i} | 〉 = B S \frac{| \cos α_{2} - \cos α_{1} |}{Δ t}$ .

При вращении замкнутого проводящего контура, помещенного в однородное магнитное поле:

угол между вектором магнитной индукции и нормалью (перпендикуляром) к контуру изменяется по закону

α = ωt,

где ω — угловая скорость вращения (циклическая частота) контура; t — время;

поток вектора магнитной индукции также зависит от времени:

Ф(t) = BS cos ωt,

где B — модуль вектора индукции магнитного поля; S — площадь ограниченной контуром площадки;

возникает ЭДС индукции, максимальное значение которой определяется выражением

$ℰ_{i \max} = ω B S$ ;

возникает ЭДС индукции, действующее (эффективное) значение которой определяется выражением

$ℰ_{д} = \frac{ℰ_{i \max}}{\sqrt{2}} = \frac{ω B S}{\sqrt{2}}$ .

Измерительные приборы (вольтметр, амперметр), подключенные к контуру, показывают именно действующие (эффективные) значения величин ЭДС и индукционного тока.

При движении проводника в однородном магнитном поле между его концами возникает разность потенциалов, значение которой равно ЭДС индукции и определяется по формуле

$ℰ_{i} = B l v \sin α$ ,

где B — модуль вектора индукции магнитного поля; l — длина проводника; v — модуль скорости движения проводника; α — угол между векторами $\vec{B}$ и $\vec{v}$ .

Пример 12. Замкнутый проводящий контур помещен в однородное магнитное поле, индукция которого с течением времени равномерно уменьшается со скоростью 0,50 Тл/с. Плоскость контура составляет угол 30° с направлением силовых линий поля, а площадь, ограниченная им, равна 100 см². Найти среднее значение ЭДС индукции, возникающей в контуре.

Решение. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.

Изменение потока вектора индукции магнитного поля определяется разностью:

∆Ф = ∆BS cos α,

где ∆B — изменение модуля индукции магнитного поля за выбранный интервал времени; S — площадь, ограниченная контуром, S = 100 см²; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура, α = 90° − 30° = 60°.

Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:

$〈 ℰ_{i} 〉 = | \frac{Δ Ф}{Δ t} | = | \frac{Δ B S \cos 60 °}{Δ t} | = \frac{Δ B S}{2 Δ t}$ ,

где ∆B/∆t — скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆B/∆t = 0,50 Тл/с.

Вычислим:

$〈 ℰ_{i} 〉 = \frac{0,50 \cdot 100 \cdot 10^{- 4}}{2} = 2,5 \cdot 10^{- 3} В = 2,5 мВ$ .

Пример 13. Проводящий контур, имеющий форму квадрата со стороной 20 см, помещен в однородное магнитное поле с индукцией 45 мТл. Плоскость контура составляет угол 30° с направлением силовых линий поля. За 0,15 с контур поворачивают таким образом, что его плоскость устанавливается перпендикулярно силовым линиям поля. Найти среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле.

Решение. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость квадрата, при повороте контура в магнитном поле.

Поток индукции магнитного поля через площадь квадрата определяется формулами:

в первом положении контура (до поворота)

Ф₁ = BS cos α₁,

где B — модуль индукции магнитного поля, B = 45 мТл; S — площадь квадрата, S = a ²; a — сторона квадрата, a = 20 см; α₁ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата в первом положении контура, α₁ = = 90° − 30° = 60°;

во втором положении контура (после поворота)

Ф₂ = BS cos α₂,

где α₂ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата во втором положении контура, α₂ = 0°.

Изменение потока вектора индукции магнитного поля определяется разностью

$Δ Ф = Ф_{2} - Ф_{1} = B S \cos 0 ° - B S \cos 60 ° = \frac{B S}{2}$ .

Среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле:

$〈 ℰ_{i} 〉 = | \frac{Δ Ф}{Δ t} | = - \frac{B S}{2 Δ t} = \frac{B a^{2}}{2 Δ t}$ ,

где ∆t — интервал времени, за который происходит поворот контура, ∆t = 0,15 с.

Расчет дает значение:

$〈 ℰ_{i} 〉 = \frac{45 \cdot 10^{- 3} \cdot {(20 \cdot 10^{- 2})}^{2}}{2 \cdot 0,15} = 6,0 \cdot 10^{- 3} В = 6,0$ мВ.

При повороте контура в нем возникает ЭДС индукции, среднее значение которой равно 6,0 мВ.

Пример 14. Скорость самолета направлена горизонтально и составляет 540 км/ч. Определить разность потенциалов, возникающую между концами крыльев самолета, если вертикальная составляющая индукции магнитного поля Земли равна 50,0 мкТл, а размах крыльев самолета равен 18,0 м.

Решение. На рисунке показано расстояние между концами крыльев самолета, направление скорости самолета и вертикальная составляющая магнитного поля Земли.

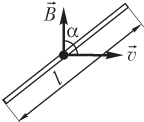
Разность потенциалов между концами проводника совпадает с электродвижущей силой индукции, которая возникает в проводнике, движущемся в магнитном поле:

∆ϕ = Blv sin α,

где B — модуль вертикальной составляющей магнитного поля Земли, B = 50,0 мкТл; l — расстояние между концами крыльев самолета, l = 18,0 м; v — модуль скорости самолета, v = 540 км/ч; α — угол между векторами $\vec{v}$ и $\vec{B}$ , показанный на рисунке, α = 90°.

Подставим указанные значения величин в формулу для расчета разности потенциалов и вычислим:

$Δ φ = 50,0 \cdot 10^{- 6} \cdot 18,0 \cdot 540 \cdot \frac{10^{3}}{3600} = 135 \cdot 10^{- 3} В = 135$ мВ.

Разность потенциалов между концами крыльев самолета при заданной в условии скорости составляет 135 мВ.

Пример 15. Замкнутая проводящая рамка вращается в однородном магнитном поле с некоторой частотой. Во сколько раз возрастет ЭДС индукции в этой рамке при увеличении частоты ее вращения на 60 %?

Решение. При вращении замкнутой проводящей рамки, помещенной в однородное магнитное поле, угол между вектором магнитной индукции и нормалью (перпендикуляром) к плоскости рамки изменяется по закону:

α = ωt,

где ω — угловая скорость вращения (циклическая частота) контура; t — время.

Поток вектора магнитной индукции, пронизывающий площадь, ограниченную рамкой, также зависит от времени:

Ф(t) = BS cos ωt,

где B — модуль вектора индукции магнитного поля; S — площадь, ограниченная рамкой.

Действующее значение ЭДС индукции определяется отношением

$ℰ_{д} = \frac{ω B S}{\sqrt{2}}$ ,

и зависит от частоты вращения рамки:

до изменения частоты вращения

$ℰ_{1 д} = \frac{ω_{1} B S}{\sqrt{2}}$ ,

где ω₁ — первоначальная циклическая частота вращения, ω₁ = 2πν₁; ν₁ — частота вращения рамки до ее изменения;

после изменения частоты вращения

$ℰ_{2 д} = \frac{ω_{2} B S}{\sqrt{2}}$ ,

где ω₂ — конечная циклическая частота вращения, ω₂ = 2πν₂; ν₂ — частота вращения рамки после ее изменения.

Искомым является отношение

$\frac{ℰ_{2 д}}{ℰ_{1 д}} = \frac{ω_{2} B S}{\sqrt{2}} \cdot \frac{\sqrt{2}}{ω_{1} B S} = \frac{ω_{2}}{ω_{1}} = \frac{ν_{2}}{ν_{1}}$ .

По условию задачи частота вращения рамки возрастает на 60 %, т.е.

ν₂ = 1,6ν₁.

Подстановка дает результат:

$\frac{ℰ_{2 д}}{ℰ_{1 д}} = \frac{1,6 ν_{1}}{ν_{1}} = 1,6$ .

При увеличении частоты вращения рамки в однородном магнитном поле на 60 % ЭДС индукции в этой рамке увеличивается в 1,6 раза.

Физика