Репетитор-онлайн — подготовка к ЦТ

9.4. Явление электромагнитной индукции

9.4.1. Поток вектора магнитной индукции, поток, сцепленный с контуром

Поток вектора магнитной индукции $\vec{B}$ через площадку, ограниченную контуром (рис. 9.19), определяется произведением

Рис. 9.19

Ф = BS cos α,

где B — модуль вектора индукции магнитного поля; S — площадь ограниченной контуром площадки; α — угол между нормалью (перпендикуляром) к площадке и вектором $\vec{B}$ .

В Международной системе единиц поток вектора магнитной индукции измеряется в веберах (1 Вб).

Поток вектора магнитной индукции через площадку, ограниченную контуром, зависит от взаимной ориентации площадки и поля, т.е. от взаимного расположения в пространстве векторов нормали (перпендикуляра) к площадке $\vec{n}$ и вектора индукции магнитного поля $\vec{B}$ :

Рис. 9.20

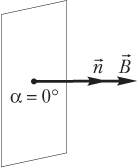
если плоскость площадки перпендикулярна полю (рис. 9.20), т.е. векторы магнитной индукции и нормали к площадке взаимно параллельны ( $\vec{n} | | \vec{B}$ ), то поток вектора магнитной индукции через данную площадку имеет максимальное значение:

Ф_max = BS;

если плоскость площадки параллельна полю (рис. 9.21), т.е. векторы магнитной индукции и вектор нормали к площадке взаимно-перпендикулярны ( $\vec{n} ⊥ \vec{B}$ ), то поток вектора магнитной индукции через данную площадку равен нулю:

Рис. 9.21

Ф = 0,

где B — модуль вектора магнитной индукции поля; S — площадь, ограниченная контуром.

Если магнитное поле образовано током, текущим в контуре, то говорят о потоке, сцепленном с данным контуром.

Поток, сцепленный с контуром, рассчитывается как произведение индуктивности контура на силу тока в данном контуре:

Ф_s = LI,

где L — индуктивность контура; I — сила тока в контуре.

В Международной системе единиц поток, сцепленный с контуром, измеряется в веберах (1 Вб).

Индуктивность контура равна отношению потока, сцепленного с данным контуром, к силе тока I в нем:

$L = \frac{Ф_{s}}{I}$ ,

где Ф_s — поток, сцепленный с контуром; I — сила тока в контуре.

В Международной системе единиц индуктивность контура измеряется в генри (1 Гн).

Индуктивность является собственной характеристикой данного контура; она зависит от геометрических размеров и формы контура и магнитных свойств среды, в которую помещен данный контур, и не зависит от силы тока в контуре.

Пример 10. Во сколько раз нужно уменьшить площадь плоского контура, чтобы при увеличении модуля индукции однородного магнитного поля на 40 % сохранить прежнее значение потока магнитной индукции? Ориентация контура остается неизменной.

Решение. Поток индукции магнитного поля через площадь, ограниченную контуром, определяется произведением:

в первом случае (до изменения величины индукции магнитного поля)

Ф₁ = B ₁S ₁ cos α₁,

где B ₁ — модуль индукции магнитного поля до ее изменения; S ₁ — площадь, ограниченная контуром, в первом случае; α₁ — угол между векторами ${\vec{B}}_{1}$ и ${\vec{n}}_{1}$ ; ${\vec{n}}_{1}$ — вектор нормали (перпендикуляра) к плоскости контура;

во втором случае (после деформации контура)

Ф₂ = B ₂S ₂ cos α₂,

где B ₂ — модуль индукции магнитного поля после ее изменения; S ₂ — площадь, ограниченная контуром, во втором случае; α₂ — угол между векторами ${\vec{B}}_{2}$ и ${\vec{n}}_{2}$ ; ${\vec{n}}_{2}$ — вектор нормали (перпендикуляра) к плоскости контура.

По условию задачи:

ориентация контура по отношению к магнитному полю не изменяется; следовательно, углы α₁ и α₂ равны между собой:

α₁ = α₂;

поток вектора магнитной индукции через площадь, ограниченную контуром, сохраняет свое значение:

Ф₁ = Ф₂.

С учетом сказанного, имеет место равенство

B ₁S ₁ = B ₂S ₂.

Отсюда следует

$\frac{S_{1}}{S_{2}} = \frac{B_{2}}{B_{1}}$ .

Модуль индукции однородного магнитного поля во втором случае превышает модуль индукции однородного магнитного поля в первом случае на 40 %, т.е. B ₂ = 1,4B ₁.

Искомое отношение площадей составляет

$\frac{S_{1}}{S_{2}} = \frac{1,4 B_{1}}{B_{1}} = 1,4$ .

Для сохранения неизменного значения потока индукции магнитного поля площадь, ограниченную контуром, необходимо уменьшить в 1,4 раза.

Пример 11. Сила тока в некотором контуре меняется по закону I = (25 + 15t) A, где t — время в секундах. Найти магнитный поток, сцепленный с контуром, в начале одиннадцатой секунды. Известно, что в начальный момент времени поток составляет 0,40 Вб.

Решение. Магнитный поток, сцепленный с контуром, определяется формулой

Ф = LI,

где L — индуктивность контура; I = (25 + 15t) — зависимость силы тока в контуре от времени; t — время.

Закон изменения потока, сцепленного с данным контуром, от времени:

Ф = L(25 + 15t).

В разные моменты времени поток, сцепленный с контуром, имеет различные значения, которые определяются следующими равенствами:

в начальный момент времени (t ₁ = 0)

Ф₁ = L(25 + 15t ₁) = L(25 + 15 ⋅ 0) = 25L;

в начале одиннадцатой секунды (t ₂ = 10 с)

Ф₂ = L(25 + 15t ₂) = L(25 + 15 ⋅ 10) = 175L.

Отношение

$\frac{Ф_{1}}{Ф_{2}} = \frac{25 L}{175 L} = \frac{1}{7}$

позволяет записать выражение для искомого значения потока

Ф₂ = 7Ф₁

и рассчитать его значение

Ф₂ = 7 ⋅ 0,40 = 2,8 Вб.

Физика