Репетитор-онлайн — подготовка к ЦТ

8.3. Закон Ома

8.3.1. Закон Ома для однородного участка цепи

Участок цепи считается однородным (рис. 8.5), если он не содержит источников тока (т.е. на участке цепи не действуют сторонние силы).

Рис. 8.5

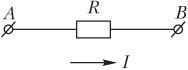
Электрический ток в однородном участке цепи появляется за счет разности потенциалов между точками A и B.

Сила тока в однородном участке цепи (см. рис. 8.5) определяется законом Ома: сила тока в однородном участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению участка:

$I = \frac{φ_{1} - φ_{2}}{R} = \frac{U}{R}$ ,

где ϕ₁ — потенциал точки A; ϕ₂ — потенциал точки B; U = ϕ₁ − ϕ₂ — напряжение на концах участка; R — общее сопротивление участка цепи.

Рис. 8.5

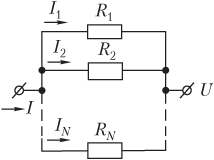
Для последовательно соединенных проводников (рис. 8.6) сила тока в каждом проводнике одинакова и определяется отношением

$I = \frac{U_{общ}}{R_{общ}}$ ,

где U _общ — напряжение на концах участка, U _общ = U ₁ + U ₂ + ... + U _N; U ₁ — падение напряжения на первом проводнике сопротивлением R ₁, U ₁ = IR ₁; U ₂ — падение напряжения на втором проводнике сопротивлением R ₂, U ₂ = IR ₂; ...; U _N — падение напряжения на N-м проводнике сопротивлением R _N, U _N = IR _N; R _общ — общее сопротивление участка, R _общ = R ₁ + R ₂ + ... + R _N.

Рис. 8.6

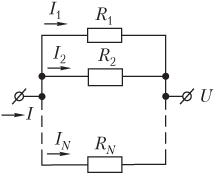
Для параллельно соединенных проводников (рис. 8.7) напряжение на каждом из проводников одинаково и равно напряжению на концах участка:

Рис. 8.7

U = I _общR _общ,

где I _общ — сила тока на всем участке, I _общ = = I ₁ + I ₂ + ... + I _N; I ₁ — сила тока в первом проводнике сопротивлением R ₁, I ₁ = U/R ₁; I ₂ — сила тока во втором проводнике сопротивлением R ₂, I ₂ = U/R ₂; ...; I _N — сила тока в N-м проводнике сопротивлением R _N, I _N = U/R _N; R _общ — общее сопротивление участка, определяемое формулой

$\frac{1}{R_{общ}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + ... + \frac{1}{R_{N}}$ .

Пример 6. Гирлянда из 25 одинаковых лампочек включена в сеть напряжением 220 В и потребляет ток силой 25 А. Определить сопротивление одной лампочки, если они включены параллельно.

Решение. Лампочки соединены параллельно, как показано на рисунке. Сопротивления лампочек одинаковы:

R ₁ = R ₂ = ... = R _N = R.

Общее сопротивление цепи определяется отношением

$R_{общ} = \frac{R}{N}$ ,

где R — сопротивление одной лампочки (искомая величина); N — количество лампочек.

Согласно закону Ома, сила тока в цепи определяется по формуле

$I = \frac{U}{R_{общ}}$ .

Подставим в записанный закон выражение для общего сопротивления

$I = \frac{N U}{R}$

и выразим искомое сопротивление

$R = \frac{N U}{I}$ .

Выполним расчет:

$R = \frac{25 \cdot 220}{25} = 220$ Ом.

Сопротивление одной лампочки составляет 220 Ом.

Пример 7. Участок цепи состоит из резистора сопротивлением 4,0 Ом, включенного последовательно резисторам сопротивлением 8,0 Ом и 16 Ом, которые соединены между собой параллельно. Определить напряжение на 4-омном резисторе, если в резисторе сопротивлением 8,0 Ом течет ток силой 10 А.

Решение. На рисунке показана схема цепи, на которой обозначены токи, протекающие в отдельных ее участках.

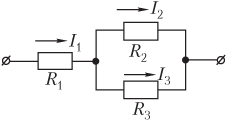
На участке сопротивлением R ₁ течет ток I ₁. Далее ток I ₁ разветвляется на две части:

на участке сопротивлением R ₂ течет ток I ₂;
на участке сопротивлением R ₃ течет ток I ₃.

Таким образом,

I ₁ = I ₂ + I ₃,

где I ₂ — сила тока в 8-омном резисторе, I ₂ = 10 А.

Участки сопротивлениями R ₂ и R ₃ соединены параллельно, поэтому падения напряжения на указанных участках одинаковы:

I ₂R ₂ = I ₃R ₃,

где R ₂ = 8,0 Ом; R ₃ = 16 Ом.

Записанные уравнения образуют систему

$\begin{array}{l} I_{1} = I_{2} + I_{3}, \\ I_{2} R_{2} = I_{3} R_{3}, \end{array}}$

позволяющую получить формулу для вычисления силы тока I ₁ в 4-омном резисторе:

$I_{1} = I_{2} (1 + \frac{R_{2}}{R_{3}})$ .

Искомое напряжение на 4-омном резисторе определяется выражением

$U = I_{1} R_{1} = I_{2} R_{1} (1 + \frac{R_{2}}{R_{3}})$ ,

где R ₁ = 4,0 Ом.

Произведем вычисление:

$U = 10 \cdot 4,0 (1 + \frac{8,0}{16}) = 60$ В.

Физика