Репетитор-онлайн — подготовка к ЦТ

7.7. Работа и энергия электростатического поля

7.7.2. Движение заряженной частицы в однородном электростатическом поле

Электростатическое поле, совершая работу, изменяет скорость и траекторию движения зарядов. Движение заряженной частицы в плоском конденсаторе (однородное электростатическое поле) наглядно иллюстрирует сказанное.

Начальная скорость частицы направлена перпендикулярно силовой линии поля

На рис. 7.24 показана положительно заряженная частица, влетающая в однородное электростатическое поле перпендикулярно силовым линиям.

Траекторией движения заряженной частицы под действием кулоновской силы (сила тяжести в этой ситуации пренебрежимо мала) является участок параболы.

Рис. 7.24

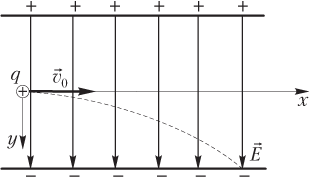
Проекции скорости частицы на координатные оси задаются следующим образом:

на горизонтальную ось —

v _x = v ₀ = const,

где v ₀ — модуль начальной скорости частицы;

вертикальную ось —

v _y = at,

где t — время движения частицы; a — модуль ускорения, вызванного кулоновской силой F _кул:

$a = \frac{F_{кул}}{m} = \frac{q E}{m}$ ,

где m — масса заряженной частицы; q — величина заряда частицы; E — модуль напряженности поля конденсатора; q/m — удельный заряд частицы.

Величина скорости заряженной частицы в произвольный момент времени определяется по формуле

$v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{v_{0}^{2} + {(\frac{q E t}{m})}^{2}}$ .

Изменения координат заряженной частицы на выходе из конденсатора определяются следующим образом:

по горизонтальной оси —

∆x = l = v ₀t,

где ∆x — смещение частицы по горизонтали; l — длина конденсатора; t — время движения частицы в конденсаторе;

вертикальной оси —

$Δ y = h = \frac{a t^{2}}{2} = \frac{q E t^{2}}{2 m}$ ,

где h — отклонение траектории частицы от первоначального направления.

Угол α, который составляет вектор скорости с его первоначальным направлением в произвольный момент времени, определяется формулой

$tg α = \frac{| v_{y} |}{v_{x}} = \frac{q E t}{m v_{0}}$ .

Начальная скорость частицы направлена под углом к силовой линии поля

На рис. 7.25 показана положительно заряженная частица, влетающая в однородное электростатическое поле под углом α к силовым линиям.

Рис. 7.25

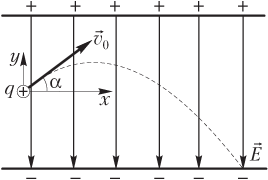
Траекторией движения частицы под действием кулоновской силы (сила тяжести в этой ситуации пренебрежимо мала) является участок параболы.

Проекции скорости частицы на координатные оси задаются следующим образом:

на горизонтальную ось —

v _x = v ₀ cos α = const,

где v ₀ — модуль начальной скорости частицы; α — угол, который составляет вектор начальной скорости частицы с горизонтом;

вертикальную ось —

v _y = v ₀ sin α − at,

где a — модуль ускорения, вызванного кулоновской силой F _кул:

$a = \frac{F_{кул}}{m} = \frac{q E}{m}$ ,

где m — масса заряженной частицы; q — величина заряда частицы; E — модуль напряженности поля конденсатора; q/m — удельный заряд частицы.

Величина скорости заряженной частицы в произвольный момент времени определяется по формуле

$v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{v_{0}^{2} \cos^{2} α + {(v_{0} \sin α - \frac{q E t}{m})}^{2}}$ .

Изменения координат заряженной частицы за промежуток времени ∆t = t от начала движения определяются следующим образом:

по горизонтальной оси —

∆x = l = v ₀t cos α,

где ∆x — смещение частицы по горизонтали;

вертикальной оси —

$Δ y = | v_{0} t \sin α - \frac{a t^{2}}{2} | = | v_{0} t \sin α - \frac{q E t^{2}}{2 m} |$ ,

где ∆y — смещение частицы по вертикали.

Угол β, который составляет вектор скорости с горизонтом в произвольный момент времени, определяется формулой

$tg β = \frac{| v_{0} \sin α - a t |}{v_{0} \cos α}$ .

Начальная скорость частицы направлена параллельно силовой линии поля

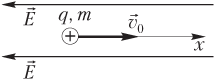
Траекторией движения положительно заряженной частицы в этом случае является прямая линия. Поэтому целесообразно рассматривать движения частицы вдоль одной из координатных осей (например, Ox); направление оси удобно выбирать по направлению начальной скорости частицы (рис. 7.26, 7.27). Силу тяжести, действующую на частицу, считаем пренебрежимо малой по сравнению с кулоновской силой F _кул.

Модуль ускорения частицы, вызванного действием кулоновской силы, определяется формулой

$a = \frac{F_{кул}}{m} = \frac{q E}{m}$ ,

где m — масса заряженной частицы; q — величина заряда частицы; E — модуль напряженности поля; q/m — удельный заряд частицы.

Проекция ускорения положительно заряженной частицы на выбранную ось может быть:

положительной, если скорость направлена по силовой линии (см. рис. 7.26);

Рис. 7.26

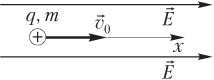
отрицательной, если скорость направлена противоположно силовой линии (см. рис. 7.27).

Рис. 7.27

Проекция скорости частицы на ось Ox изменяется с течением времени по закону

v _x(t) = v ₀ + a _xt,

где a _x — проекция ускорения на выбранную ось:

$a_{x} = \pm \frac{q E}{m}$ .

Модуль скорости заряженной частицы в произвольный момент времени определяется по формуле

$v = | v_{0} \pm \frac{q E t}{m} |$ .

Изменение координаты заряженной частицы за промежуток времени ∆t = t от начала движения (модуль перемещения) определяется следующим образом:

$Δ x = | x - x_{0} | = | v_{0} t \pm \frac{q E t^{2}}{m} |$ .

Пример 23. Заряженная частица с удельным зарядом 20,0 мКл/кг влетает со скоростью 10,0 м/с в плоский конденсатор перпендикулярно силовым линиям электростатического поля конденсатора, величина напряженности которого равна 300 В/м. Длина обкладок конденсатора составляет 8,00 мм. Пренебрегая силой тяжести частицы, найти ее смещение на выходе из конденсатора.

Решение. На рисунке показано направление силовых линий электростатического поля конденсатора и направление вектора скорости заряженной частицы.

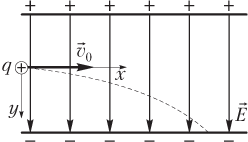
Уравнения движения заряженной частицы в электростатическом поле задаются следующими выражениями:

по горизонтальной оси Ox —

x = v ₀ _xt = v ₀t,

где v ₀ _x — проекция начальной скорости частицы на указанную ось, v ₀ _x = v ₀ = const; v ₀ — модуль начальной скорости частицы; t — время;

вертикальной оси Oy —

$y = v_{0 y} t + \frac{a_{y} t^{2}}{2} = \frac{a t^{2}}{2}$ ,

где v ₀ _y — проекция начальной скорости частицы на указанную ось, v ₀ _y = 0; a _y — проекция ускорения частицы на указанную ось, a _y = a; a — модуль ускорения.

Модуль ускорения, вызванного кулоновской силой F _кул, определяется формулой

$a = \frac{F_{кул}}{m} = \frac{q E}{m}$ ,

где q/m — удельный заряд частицы; E — величина напряженности электростатического поля конденсатора.

Пусть частица движется в конденсаторе в течение времени t = τ. Тогда на выходе из конденсатора ее координаты имеют следующие значения:

горизонтальная координата —

x = v ₀τ = l,

где l — длина обкладок конденсатора;

вертикальная координата —

$y = \frac{a τ^{2}}{2} = h$ ,

где h — смещение частицы от первоначального направления (искомая величина).

Записанные уравнения образуют систему, которая с учетом выражения для модуля ускорения приобретает вид

$\begin{array}{l} v_{0} τ = l, \\ \frac{q E τ^{2}}{2 m} = h . \end{array}}$

Решение системы относительно h дает формулу

$h = \frac{q E τ^{2}}{2 m} = \frac{q E l^{2}}{2 m v_{0}^{2}}$ .

Вычислим значение смещения частицы от первоначального направления:

$h = \frac{20,0 \cdot 10^{- 3} \cdot 300 \cdot {(8,00 \cdot 10^{- 3})}^{2}}{2 \cdot 10^{2}} = 1,92 \cdot 10^{- 6} м = 1,92$ мкм.

Смещение заряженной частицы от первоначального направления за время движения в конденсаторе составляет 1,92 мкм.

Физика