Репетитор-онлайн — подготовка к ЦТ

7.7. Работа и энергия электростатического поля

7.7.1. Работа сил электростатического поля по перемещению заряда

Работу сил электростатического поля можно рассчитать двумя способами в зависимости от того, является поле однородным или неоднородным.

В однородном электростатическом поле работа сил поля по перемещению заряда q определяется формулой

$A = (\vec{F}, Δ \vec{r}) = \vec{F} \cdot Δ \vec{r} = F Δ r \cos α$ ,

где $\vec{F}$ — сила, действующая на заряд q со стороны поля, $\vec{F} = q \vec{E}$ ; q — заряд; $\vec{E}$ — напряженность поля; $Δ \vec{r}$ — перемещение заряда; α — угол между векторами $\vec{F}$ и $Δ \vec{r}$ ;

В однородном поле сила, действующая на заряд, является постоянной величиной, так как вектор $\vec{E}$ имеет одинаковое значение и направление в любой точке поля).

При перемещении электрического заряда:

вдоль силовой линии электростатическим полем совершается максимальная положительная работа —

$A = q E Δ r \cos 0 ° = q E Δ r$ ;

противоположно силовой линии электростатическим полем совершается максимальная отрицательная работа —

$A = q E Δ r \cos 180 ° = - q E Δ r$ ;

перпендикулярно силовой линии электростатическим полем работа не совершается —

$A = q E Δ r \cos 90 ° = 0$ .

В любом ( в том числе в неоднородном) электростатическом поле работа сил поля не зависит от траектории перемещения заряда и может быть рассчитана по формуле

A = q(φ₁ − φ₂),

где φ₁ — потенциал точки поля, в которой заряд q находился в начальный момент времени; φ₂ — потенциал точки поля, в которой заряд q оказался в результате перемещения.

При перемещении электрического заряда по эквипотенциальной поверхности (φ₁ = φ₂) электростатическим полем работа не совершается:

A = q(φ₁ − φ₂) = 0.

В любом электростатическом поле (однородном и неоднородном) работа по перемещению электрического заряда может быть рассчитана графически как площадь трапеции (рис. 7.23) по графику зависимости проекции силы на направление перемещения F _r(r).

Рис. 7.23

Пример 21. Какую работу совершит однородное электростатическое поле напряженностью 300 В/м при перемещении заряда 5,00 мкКл на 50,0 мм в направлении, составляющем угол 120° с направлением силовых линий?

Решение. На рисунке показаны линии вектора напряженности однородного электростатического поля $\vec{E}$ и перемещаемый в данном поле заряд q. Перемещение заряда происходит из точки 1 в точку 2.

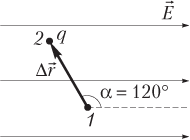
Работа сил однородного электростатического поля по перемещению точечного заряда определяется формулой

$A = q E | Δ \vec{r} | \cos α$ ,

где q — заряд, совершающий перемещение в указанном поле; E — модуль вектора напряженности поля; $| Δ \vec{r} |$ — величина перемещения; α — угол между направлениями векторов напряженности и перемещения.

Угол между векторами $\vec{E}$ и $Δ \vec{r}$ составляет 120°, поэтому

$A = q E | Δ \vec{r} | \cos 120 ° = - 0,5 q E | Δ \vec{r} |$ .

Расчет дает значение

A = −0,5 ⋅ 5,00 ⋅ 10⁻⁶ ⋅ 300 ⋅ 50,0 ⋅ 10⁻³ =

= −37,5 ⋅ 10⁻⁶ Дж = −37,5 мкДж.

При перемещении заряда в указанном направлении совершается отрицательная работа –37,5 мкДж, так как угол между направлением силовых линий и направлением перемещения является тупым.

Пример 22. Точечный заряд 3 мкКл расположен в начале прямоугольной системы координат xOy, где x и y заданы в метрах. Какую работу совершает электростатическое поле, образованное данным зарядом, при перемещении другого точечного заряда 2 мкКл из точки (5; 0) в точку (0; 5)? Система зарядов находится в вакууме.

Решение. На рисунке показаны линии вектора напряженности электростатического поля $\vec{E}$ , образованного точечным положительным зарядом Q, расположенным в начале системы координат. Перемещение $Δ \vec{r}$ другого точечного заряда q происходит из точки с координатами (5; 0) в точку с координатами (0; 5).

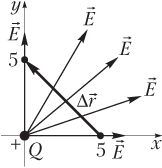
Электростатическое поле, образованное точечным зарядом, является неоднородным. Поэтому для вычисления работы сил поля используем формулу

A = q(φ₁ − φ₂),

где q — заряд, перемещаемый в поле; φ₁ — потенциал электростатического поля, образованного зарядом Q в точке (5; 0); φ₂ — потенциал электростатического поля, образованного зарядом Q в точке (0; 5).

Потенциал электростатического поля, образованного зарядом Q, задается следующими выражениями:

для точки (5; 0) —

$φ_{1} = \frac{k Q}{r_{1}}$ ,

где k — коэффициент пропорциональности, k = 9 ⋅ 10⁹ Н ⋅ м²/Кл²; r ₁ — расстояние от заряда Q до точки с координатами (5, 0), r ₁ = 5 м;

для точки (0; 5) —

$φ_{2} = \frac{k Q}{r_{2}}$ ,

где r ₂ — расстояние от заряда Q до точки с координатами (0, 5), r ₂ = 5 м.

С учетом выражений для потенциалов формула для вычисления работы приобретает следующий вид:

$A = q (\frac{k Q}{r_{1}} - \frac{k Q}{r_{2}}) = k q Q (\frac{1}{r_{1}} - \frac{1}{r_{2}})$ .

Подстановка числовых данных дает результат:

$A = 9 \cdot 10^{9} \cdot 3 \cdot 10^{- 6} \cdot 2 \cdot 10^{- 6} \cdot (\frac{1}{5} - \frac{1}{5}) = 0$ .

При перемещении заряда между точками с указанными координатами электростатическое поле не совершает работу, так как точки находятся на одинаковом расстоянии от заряда, создающего данное поле.

Физика