Репетитор-онлайн — подготовка к ЦТ

7.7. Работа и энергия электростатического поля

7.7.3. Энергия электростатического поля

Энергия однородного поля, заряженного конденсатора и уединенного проводника

Энергия однородного электростатического поля определяется значением его напряженности E, объемом пространства V, занятого полем, и электрическими свойствами пространства (ε₀, ε):

$W = \frac{ε_{0} ε E^{2} V}{2}$ ,

где ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды.

Объемная плотность энергии однородного электростатического поля (энергия единицы объема):

$W = \frac{W}{V} = \frac{ε_{0} ε E^{2}}{2}$ .

Энергия электростатического поля заряженного конденсатора может быть рассчитана по одной из трех формул:

$W = \frac{C U^{2}}{2}$ , $W = \frac{Q^{2}}{2 C}$ , $W = \frac{Q U}{2}$ ,

где C — емкость конденсатора; U — разность потенциалов (напряжение) между обкладками конденсатора; Q — заряд на его обкладках.

Энергия электростатического поля заряженного уединенного проводника может быть рассчитана по одной из трех формул:

$W = \frac{C φ^{2}}{2}$ , $W = \frac{Q^{2}}{2 C}$ , $W = \frac{Q φ}{2}$ ,

где C — емкость уединенного проводника; φ — потенциал уединенного проводника; Q — заряд уединенного проводника.

Энергия электростатического взаимодействия

Энергия электростатического взаимодействия заряда и поля (потенциальная энергия точечного заряда q в электростатическом поле) определяется формулой

W = qφ,

где φ — потенциал той точки поля, в которую помещен заряд q.

Потенциальная энергия электростатического взаимодействия двух точечных зарядов вычисляется по формуле

$W = \frac{k q_{1} q_{2}}{ε r}$ ,

где k — коэффициент пропорциональности $k = \frac{1}{4 π ε_{0}} \approx 9 \cdot 10^{9}$ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); q ₁, q ₂ — взаимодействующие заряды; ε — диэлектрическая проницаемость среды; r — расстояние между зарядами.

Энергия взаимодействия двух точечных зарядов:

положительна, если заряды имеют одинаковые знаки; в этом случае говорят о потенциальной энергии отталкивания;
отрицательна, если заряды имеют противоположные знаки; в этом случае говорят о потенциальной энергии притяжения.

Потенциальная энергия электростатического взаимодействия нескольких точечных зарядов вычисляется по формуле

$W = \frac{1}{2} (q_{1} φ_{1} + q_{2} φ_{2} + ... + q_{n} φ_{n})$ ,

где φ₁ — потенциал той точки поля, в которую помещен заряд q ₁ (создается всеми зарядами, кроме q ₁); φ₂ — потенциал той точки поля, в которую помещен заряд q ₂ (создается всеми зарядами, кроме q ₂); …; φ_n — потенциал той точки поля, в которую помещен заряд q _n (создается всеми зарядами, кроме q _n).

Электростатическое поле изменяет механическую энергию движущейся в нем заряженной частицы:

$\frac{m v_{2}^{2}}{2} - \frac{m v_{1}^{2}}{2} = q (φ_{1} - φ_{2})$ ,

где m — масса частицы; q — заряд частицы; v ₁ — модуль скорости частицы в точке поля с потенциалом φ₁; v ₂ — модуль скорости частицы в точке поля с потенциалом φ₂.

Пример 24. В вершинах правильного треугольника со стороной 300 мм находятся одинаковые точечные заряды по 30 мкКл каждый. Заряды удерживаются нитями одинаковой длины и находятся в воздухе. Найти максимальную кинетическую энергию каждого из зарядов, если одновременно пережечь нити.

Решение. На рисунке показаны заряды q ₁ = q ₂ = q ₃ = q, расположенные в вершинах равностороннего треугольника со стороной a.

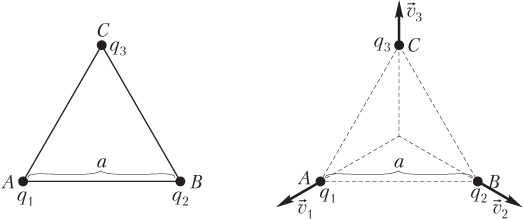
Рассчитаем потенциальную энергию взаимодействия зарядов. Для этого найдем потенциал электростатического поля, созданного указанными зарядами, в вершинах треугольника.

Каждый из зарядов, расположенных в одной из вершин треугольника, создает электростатическое поле в двух других вершинах, потенциал которого определяется формулами:

заряд q ₁ в вершинах B и C —

$φ_{1} = \frac{k q_{1}}{r_{1}} = \frac{k q}{a}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; q ₁ — заряд, расположенный в вершине A, q ₁ = q; r ₁ — расстояние от заряда q ₁ до каждой из вершин B и C, r ₁ = a;

заряд q ₂ в вершинах A и C —

$φ_{2} = \frac{k q_{2}}{r_{2}} = \frac{k q}{a}$ ,

где q ₂ — заряд, расположенный в вершине B, q ₂ = q; r ₂ — расстояние от заряда q ₂ до каждой из вершин A и C, r ₂ = a;

заряд q ₃ в вершинах A и B —

$φ_{3} = \frac{k q_{3}}{r_{3}} = \frac{k q}{a}$ ,

где q ₃ — заряд, расположенный в вершине C, q ₃ = q; r ₃ — расстояние от заряда q ₃ до каждой из вершин A и B, r ₃ = a.

Потенциал электростатического поля в определенной вершине треугольника складывается из потенциалов полей, созданных зарядами, помещенными в остальные вершины:

в вершине A (поле создается зарядами q ₂ и q ₃) —

$φ_{A} = φ_{2} + φ_{3} = \frac{k q}{a} + \frac{k q}{a} = \frac{2 k q}{a}$ ;

вершине B (поле создается зарядами q ₁ и q ₃) —

$φ_{B} = φ_{1} + φ_{3} = \frac{k q}{a} + \frac{k q}{a} = \frac{2 k q}{a}$ ;

вершине C (поле создается зарядами q ₁ и q ₂) —

$φ_{C} = φ_{1} + φ_{2} = \frac{k q}{a} + \frac{k q}{a} = \frac{2 k q}{a}$ .

Потенциальная энергия взаимодействия зарядов определяется формулой

$W_{p} = \frac{1}{2} (q_{1} φ_{A} + q_{2} φ_{B} + q_{3} φ_{C}) = \frac{1}{2} (q \frac{2 k q}{a} + q \frac{2 k q}{a} + q \frac{2 k q}{a}) = \frac{3 k q^{2}}{a}$ .

При пережигании нитей одноименные заряды отталкиваются и разлетаются симметрично в разные стороны. Потенциальная энергия электростатического взаимодействия зарядов переходит в кинетическую энергию их движения. На достаточно большом удалении зарядов друг от друга они перестают взаимодействовать, и потенциальная энергия полностью переходит в кинетическую:

W _p = W _k.

В силу симметричного расположения зарядов кинетическая энергия системы поровну делится на три части — каждый из зарядов имеет энергию

$W_{k 0} = \frac{1}{3} W_{k} = \frac{1}{3} W_{p} = \frac{1}{3} \cdot \frac{3 k q^{2}}{a} = \frac{k q^{2}}{a}$ .

Вычислим:

$W_{k 0} = \frac{9,0 \cdot 10^{9} {(30 \cdot 10^{- 6})}^{2}}{300 \cdot 10^{- 3}} = 27$ Дж.

Физика