Физика

Пример 17. Два конденсатора одинаковой электроемкости заряжены до разности потенциалов 120 и 240 В соответственно, а затем соединены одноименно заряженными пластинами. Какова станет разность потенциалов между обкладками конденсаторов после указанного соединения?

Решение. До соединения одноименных пластин конденсаторов каждый из них обладал зарядом:

• первый конденсатор —

Q ₁ = C ₁U ₁ = CU ₁,

где C ₁ — электроемкость первого конденсатора, C ₁ = C; U ₁ — разность потенциалов между обкладками первого конденсатора;

• второй конденсатор —

Q ₂ = C ₂U ₂ = CU ₂,

где C ₂ — электроемкость второго конденсатора, C ₂ = C; U ₂ — разность потенциалов между обкладками второго конденсатора.

При соединении одноименных обкладок получим параллельное соединение конденсаторов. Разность потенциалов между обкладками батареи конденсаторов определяется формулой

$U=\frac{Q_{\text{общ}}}{C_{\text{общ}}}$,

где Q _общ — общий заряд батареи; C _общ — общая электроемкость батареи.

Общий заряд батареи двух конденсаторов, полученной соединением их одноименных обкладок, определяется суммой зарядов каждого из них:

Q _общ = Q ₁ + Q ₂,

а общая электроемкость батареи двух одинаковых конденсаторов, соединенных параллельно, —

C _общ = C ₁ + C ₂ = 2C.

Следовательно, разность потенциалов между обкладками батареи определяется выражением

$U=\frac{Q_{\text{общ}}}{C_{\text{общ}}}=\frac{Q_1+Q_2}{2C}=\frac{C{U}_1+C{U}_2}{2C}=\frac{U_1+U_2}{2}$.

Вычислим:

$U=\frac{120+240}{2}=180$ В.

Разность потенциалов между обкладками конденсаторов после указанного соединения составит 180 В.

Пример 18. Два одинаковых плоских конденсатора заряжены до разности потенциалов 200 и 300 В. Определить разность потенциалов между обкладками конденсаторов после соединения их разноименных обкладок.

Решение. До соединения разноименных пластин конденсаторов каждый из них обладал зарядом:

• первый конденсатор —

Q ₁ = C ₁U ₁ = CU ₁,

где C ₁ — электроемкость первого конденсатора, C ₁ = C; U ₁ — разность потенциалов между обкладками первого конденсатора;

• второй конденсатор —

Q ₂ = C ₂U ₂ = CU ₂,

где C ₂ — электроемкость второго конденсатора, C ₂ = C; U ₂ — разность потенциалов между обкладками второго конденсатора.

При соединении разноименных обкладок получаем параллельное соединение конденсаторов. Разность потенциалов между обкладками батареи конденсаторов определяется формулой

$U=\frac{Q_{\text{общ}}}{C_{\text{общ}}}$,

где Q _общ — общий заряд батареи; C _общ — общая электроемкость батареи.

Общий заряд батареи двух конденсаторов, полученной соединением их разноименных обкладок, определяется модулем разности зарядов каждого из них:

Q _общ = |Q ₁ − Q ₂|,

а общая электроемкость батареи двух одинаковых конденсаторов, соединенных параллельно, —

C _общ = C ₁ + C ₂ = 2C.

Следовательно, разность потенциалов между обкладками батареи определяется выражением

$U=\frac{Q_{\text{общ}}}{C_{\text{общ}}}=\frac{\left|Q_1-Q_2\right|}{2C}=\frac{\left|C{U}_1-C{U}_2\right|}{2C}=\frac{\left|U_1-U_2\right|}{2}$.

Вычислим:

$U=\frac{\left|200-300\right|}{2}=50$ В.

Разность потенциалов между обкладками конденсаторов после указанного соединения составит 50 В.

Пример 19. Плоский воздушный конденсатор заряжен до 180 В и отключен от источника напряжения. В пространство между его обкладками, параллельно им, вводят незаряженную металлическую пластину, толщина которой в 3 раза меньше расстояния между обкладками. Считая, что металлическая пластина расположена симметрично относительно обкладок конденсатора, определить разность потенциалов, которая установится между ними.

Решение. При помещении металлической пластины в плоский конденсатор так, как показано на рисунке, свободные электроны в металле перераспределяются:

• плоскость, обращенная к положительно заряженной обкладке конденсатора, получает избыток электронов и заряжается отрицательным зарядом q ₁ = −q;

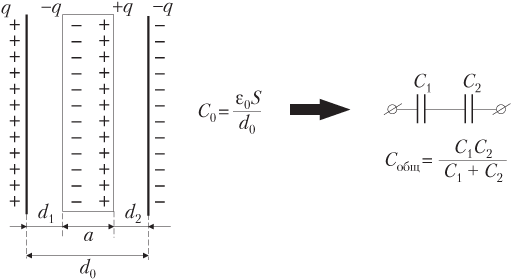
• плоскость, обращенная к отрицательно заряженной обкладке конденсатора, имеет недостаток электронов и заряжается положительным зарядом q ₂ = +q.

В результате перераспределения заряда пластина остается нейтральной:

Q = q ₁ + q ₂ = −q + q = 0.

Перераспределение заряда в металлической пластине приводит к образованию батареи двух конденсаторов:

• положительно заряженная обкладка конденсатора и отрицательно заряженная плоскость металлической пластины имеют одинаковые по модулю заряды противоположного знака; они могут рассматриваться как конденсатор с электроемкостью

$C_1=\frac{{\epsilon }_{0}S}{d_1}$,

где ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); S — площадь обкладки конденсатора; d ₁ — расстояние между положительно заряженной обкладкой конденсатора и отрицательно заряженной плоскостью металлической пластины;

• отрицательно заряженная обкладка конденсатора и положительно заряженная плоскость металлической пластины также имеют одинаковые по модулю заряды противоположного знака; они могут рассматриваться как конденсатор с электроемкостью

$C_2=\frac{{\epsilon }_{0}S}{d_2}$,

где d ₂ — расстояние между отрицательно заряженной обкладкой конденсатора и положительно заряженной плоскостью металлической пластины.

Оба конденсатора имеют одинаковые заряды и образуют последовательное соединение. Электроемкость батареи двух конденсаторов при последовательном соединении определяется формулой

$\frac{1}{C_{\text{общ}}}=\frac{1}{C_1}+\frac{1}{C_2}$, или $C_{\text{общ}}=\frac{C_1{C}_2}{C_1+C_2}$.

При симметричном расположении пластины в пространстве между обкладками конденсатора (d ₁ = d ₂ = d) электроемкости конденсаторов одинаковы:

$C_1=C_2=\frac{{\epsilon }_{0}S}{d}$,

общая электроемкость батареи задается выражением

$C_{\text{общ}}=\frac{C_1{C}_2}{C_1+C_2}=\frac{C}{2}=\frac{{\epsilon }_{0}S}{2d}$,

где d = (d ₀ − a)/2; d ₀ — расстояние между обкладками конденсатора до введения пластины; a — толщина металлической пластины.

Разность потенциалов между обкладками батареи

$U=\frac{Q_{\text{общ}}}{C_{\text{общ}}}=\frac{2dq}{{\epsilon }_{0}S}=\frac{q(d_0-a)}{{\epsilon }_{0}S}$,

где Q _общ — заряд батареи последовательно соединенных конденсаторов, Q _общ = q.

Первоначальная разность потенциалов определяется формулой

$U_0=\frac{Q_0}{C_0}=\frac{Q_0{d}_0}{{\epsilon }_{0}S}$,

где Q ₀ — заряд конденсатора до введения пластины, Q ₀ = q (конденсатор отключен от источника напряжения); C ₀ — электроемкость конденсатора до введения пластины.

Отношение разности потенциалов до и после введения металлической пластины определяется выражением

$\frac{U}{U_0}=\frac{d_0-a}{d_0}$.

Отсюда найдем искомую разность потенциалов

$U=U_0\frac{d_0-a}{d_0}$.

С учетом d ₀ = 3a выражение принимает вид:

$U=U_0\frac{3a-a}{3a}=\frac{2}{3}{U}_0$.

Рассчитаем:

$U=\frac{2}{3}\cdot 180=120$ В.

В результате введения в конденсатор металлической пластины разность потенциалов между его обкладками уменьшилась и составила 120 В.

Пример 20. Плоский воздушный конденсатор заряжен до 240 В и отключен от источника напряжения. Его вертикально погружают в некоторую жидкость с диэлектрической проницаемостью 2,00 на одну треть объема. Найти разность потенциалов, которая установится между обкладками конденсатора.

Решение. При частичном погружении плоского воздушного конденсатора в жидкий диэлектрик, как показано на рисунке, свободные электроны на его обкладках перераспределяются таким образом, что:

• часть обкладок конденсатора, погруженная в диэлектрик, имеет заряд q ₁;
• часть обкладок конденсатора, оставшаяся в воздухе, имеет заряд q ₂.

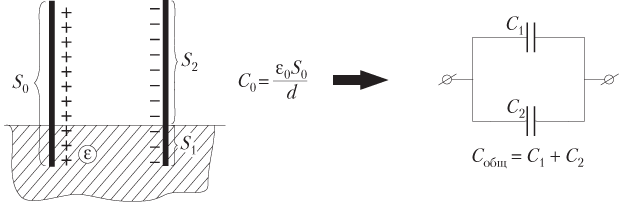
В результате перераспределения заряда по площади обкладок конденсатора на его обкладках устанавливается заряд:

Q _общ = q ₁ + q ₂.

Площадь обкладок конденсатора при частичном погружении его в жидкий диэлектрик разделяется на две части:

• часть, погруженная в диэлектрик, имеет площадь S ₁; соответствующая часть конденсатора может рассматриваться как отдельный конденсатор с электроемкостью

$C_1=\frac{{\epsilon }_0\epsilon S_1}{d}$,

где ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость конденсатора; d — расстояние между обкладками конденсатора;

• часть, оставшаяся в воздухе, имеет площадь S ₂; соответствующая часть конденсатора может рассматриваться как отдельный конденсатор с электроемкостью

$C_2=\frac{{\epsilon }_0{S}_2}{d}$.

Оба конденсатора обладают одинаковой разностью потенциалов между обкладками и образуют параллельное соединение. Электроемкость батареи двух конденсаторов при параллельном соединении определяется формулой

$C_{\text{общ}}=C_1+C_2=\frac{{\epsilon }_0\epsilon S_1}{d}+\frac{{\epsilon }_0{S}_2}{d}=\frac{{\epsilon }_0}{d}(\epsilon S_1+S_2)$,

а заряд на обкладках батареи —

$Q_{\text{общ}}=C_{\text{общ}}U=\frac{{\epsilon }_0}{d}(\epsilon S_1+S_2)U$,

где U — разность потенциалов между обкладками батареи.

Электроемкость конденсатора до погружения его в диэлектрик определяется выражением

$C_0=\frac{{\epsilon }_0{S}_0}{d}$,

а заряд на его обкладках —

$Q_0=C_0{U}_0=\frac{{\epsilon }_0{S}_0}{d}{U}_0$,

где U ₀ — разность потенциалов между обкладками конденсатора до введения пластины; S ₀ — площадь обкладки.

Конденсатор отключен от источника напряжения, поэтому его заряд после частичного погружения в диэлектрик не изменяется:

Q ₀ = Q _общ,

или, в явном виде,

$\frac{{\epsilon }_0{S}_0}{d}{U}_0=\frac{{\epsilon }_0}{d}(\epsilon S_1+S_2)U$.

После упрощения имеем:

S ₀U ₀ = (εS ₁ + S ₂)U.

Отсюда следует, что искомая разность потенциалов определяется выражением

$U=U_0\frac{S_0}{\epsilon S_1+S_2}$.

С учетом того, что в диэлектрик погружена часть пластин конденсатора, т.е.

S ₁ = ηS ₀, S ₂ = S ₀ − S ₁ = S ₀ − ηS ₀ = S ₀(1 − η), $\eta =\frac{1}{3}$,

получим:

$U=U_0\frac{S_0}{\epsilon \eta S_0+S_0(1-\eta )}=\frac{U_0}{\epsilon \eta +1-\eta }$.

Отсюда найдем искомую разность потенциалов:

$U=\frac{240}{\mathrm{2,00}\cdot \frac{1}{3}+1-\frac{1}{3}}=180$ В.