Репетитор-онлайн — подготовка к ЦТ

7.6. Конденсаторы

7.6.1. Электроемкость конденсатора и уединенного проводника

Конденсатор представляет собой два разноименно заряженных проводника (обкладки), находящихся на небольшом расстоянии друг от друга. Заряды обкладок равны по модулю и противоположны по знаку.

Электроемкость конденсатора определяется отношением

$C = \frac{Q}{φ_{1} - φ_{2}} = \frac{Q}{U}$ ,

где Q — заряд конденсатора (зарядом конденсатора принято считать заряд положительной обкладки); U — разность потенциалов между его обкладками, U = φ₁ − φ₂.

Электроемкость данного конденсатора

зависит от геометрических параметров конденсатора и электрических свойств среды, заполняющей пространство между его обкладками;
не зависит от заряда на его обкладках и разности потенциалов между ними.

В Международной системе единиц электрическая емкость измеряется в фарадах (1 Ф).

По форме проводящих поверхностей (обкладок) различают плоские, цилиндрические и сферические конденсаторы.

Плоский конденсатор представляет собой две параллельные пластины, заряженные одинаковыми по модулю, но противоположными по знаку зарядами (рис. 7.18).

Рис. 7.18

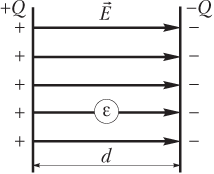
Электроемкость плоского конденсатора определяется формулой

$C = \frac{ε_{0} ε S}{d}$ ,

где ε₀ — электрическая постоянная, ε₀ = = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды, заполняющей пространство между обкладками конденсатора; S — площадь одной из обкладок конденсатора; d — расстояние между обкладками.

Поле в плоском конденсаторе является однородным.

Цилиндрический конденсатор представляет собой два коаксиальных цилиндра (цилиндры с общей осью), заряженных одинаковыми по модулю, но противоположными по знаку зарядами (рис. 7.19).

Рис. 7.19

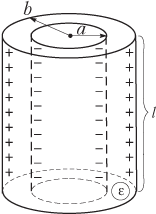
Емкость цилиндрического конденсатора определяется формулой

$C = \frac{2 π ε_{0} ε l}{\ln (b / a)}$ ,

где ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды, заполняющей пространство между обкладками конденсатора; l — длина цилиндра; a, b — радиусы внутреннего и внешнего цилиндров соответственно.

Сферический конденсатор представляет собой две концентрические сферы (сферы с общим центром), заряженные одинаковыми по модулю, но противоположными по знаку зарядами (рис. 7.20).

Рис. 7.20

Электроемкость сферического конденсатора определяется формулой

$C = \frac{4 π ε_{0} ε}{1 / a - 1 / b}$ ,

где ε₀ — электрическая постоянная, ε₀ = = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды, заполняющей пространство между обкладками конденсатора; a, b — радиусы внутренней и внешней сфер соответственно.

Электроемкость уединенного проводника определяется отношением

$C = \frac{Q}{φ}$ ,

где Q — заряд уединенного проводника; φ — потенциал уединенного проводника. Проводник считается уединенным, если он расположен на значительном расстоянии от других тел, которые могут повлиять на его электрические свойства.

Электроемкость данного уединенного проводника:

зависит от геометрических параметров проводника и электрических свойств среды, в которую этот проводник помещен;
не зависит от заряда и потенциала проводника.

Электроемкость уединенного шара радиусом R определяется формулой

C = 4πε₀εR,

где ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды, в которой находится уединенный шар.

Пример 15. Во сколько раз уменьшится электроемкость плоского конденсатора при увеличении расстояния между пластинами в 3,0 раза и одновременном уменьшении объема между ними в 4,0 раза?

Решение. При изменении габаритов конденсатора (расстояния между обкладками и объема пространства, занятого полем) изменяется его электроемкость.

Электроемкость плоского конденсатора определяется следующими формулами:

до изменения габаритов (начальное состояние) —

$C_{1} = \frac{ε_{0} ε S_{1}}{d_{1}}$ ,

где ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды, заполняющей пространство между обкладками; S ₁ — площадь одной из обкладок конденсатора; d ₁ — расстояние между обкладками;

после изменения габаритов (конечное состояние) —

$C_{2} = \frac{ε_{0} ε S_{2}}{d_{2}}$ ,

где S ₂ — площадь одной из обкладок конденсатора после изменения объема пространства между ними; d ₂ — новое расстояние между обкладками.

Искомой величиной является отношение (C ₁/C ₂):

$\frac{C_{1}}{C_{2}} = \frac{ε ε_{0} S_{1}}{d_{1}} \cdot \frac{d_{2}}{ε ε_{0} S_{2}} = \frac{S_{1}}{S_{2}} \cdot \frac{d_{2}}{d_{1}}$ .

Установим, как изменяется площадь пластин при изменении объема пространства между обкладками конденсатора. Для этого запишем указанный объем в виде произведения:

V = d ⋅ S.

Отсюда следует, что площади обкладок конденсатора определяются следующими выражениями:

до изменения габаритов (начальное состояние) —

$S_{1} = \frac{V_{1}}{d_{1}}$ ,

где V ₁ — первоначальный объем пространства между обкладками конденсатора;

после изменения габаритов (конечное состояние) —

$S_{2} = \frac{V_{2}}{d_{2}}$ ,

V ₂ — новый объем пространства между обкладками конденсатора.

Отношение площадей

$\frac{S_{1}}{S_{2}} = \frac{V_{1}}{d_{1}} \cdot \frac{d_{2}}{V_{2}}$

позволяет получить формулу для расчета искомой величины

$\frac{C_{1}}{C_{2}} = \frac{V_{1}}{d_{1}} \cdot \frac{d_{2}}{V_{2}} \cdot \frac{d_{2}}{d_{1}} = \frac{V_{1}}{V_{2}} \cdot {(\frac{d_{2}}{d_{1}})}^{2}$ .

С учетом заданных в условии задачи изменений объема

V ₁ = 4,0V ₂

и расстояния между его обкладками

d ₂ = 3,0d ₁

полученное отношение электроемкостей конденсатора преобразуется к виду

$\frac{C_{1}}{C_{2}} = \frac{4,0 V_{2}}{V_{2}} \cdot {(\frac{3,0 d_{1}}{d_{1}})}^{2} = 4,0 \cdot {(3,0)}^{2} = 36$ .

При заданном изменении габаритов конденсатора его электроемкость уменьшается в 36 раз.

Физика