Репетитор-онлайн — подготовка к ЦТ

7.5. Принцип суперпозиции электростатических полей

7.5.2 Принцип суперпозиции для потенциала

Принцип суперпозиции для потенциала позволяет рассчитать потенциал поля, образованного несколькими заряженными объектами.

Потенциал φ результирующего электростатического поля, образованного несколькими зарядами в заданной точке пространства, рассчитывается как сумма потенциалов полей, образованных каждым из зарядов в отдельности:

φ = φ₁ + φ₂ + … + φ_n,

где φ₁ — потенциал поля, образованного первым зарядом; φ₂ — потенциал поля, образованного вторым зарядом; …; φ_n — потенциал поля, образованного n-м зарядом.

Для того чтобы рассчитать потенциал поля, созданного несколькими зарядами Q ₁, Q ₂, …, Q _n в заданной точке пространства, используют следующий алгоритм:

1) записывают потенциалы полей, образованных каждым из зарядов Q ₁, Q ₂, …, Q _n (в отдельности) с учетом знака зарядов:

φ₁, φ₂, …, φ_n,

где φ₁ — потенциал поля, образованного первым зарядом; φ₂ — потенциал поля, образованного вторым зарядом; …; φ_n — потенциал поля, образованного n-м зарядом;

2) вычисляют потенциал результирующего поля как алгебраическую сумму записанных выше потенциалов:

φ = φ₁ + φ₂ + … + φ_n.

Пример 12. Два точечных заряда q ₁ = 5 мкКл и q ₂ = −2 мкКл находятся в точках (5; 0) и (0; 2) прямоугольной системы координат xOy, где координаты x, y выражены в метрах. Рассчитать потенциал результирующего поля в начале системы координат, если диэлектрическая проницаемость среды равна единице.

Решение. На рисунке показана система координат и заряды, расположенные в точках с заданными координатами. Потенциал результирующего электростатического поля в начале системы координат представляет собой алгебраическую сумму

φ = φ₁ + φ₂,

где φ₁ — потенциал поля, образованного первым зарядом; φ₂ — потенциал поля, образованного вторым зарядом.

Рассчитаем потенциал результирующего поля в начале системы координат, пользуясь алгоритмом:

1) потенциалы полей, созданных каждым из зарядов в отдельности, определяются следующими формулами:

поля, образованного зарядом q ₁, —

$φ_{1} = \frac{k q_{1}}{r_{1}}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; q ₁ — заряд, расположенный в точке с координатами (5; 0); r ₁ — расстояние от заряда q ₁ до начала системы координат, r ₁ = 5 м;

поля, образованного зарядом q ₂, —

$φ_{2} = \frac{k q_{2}}{r_{2}}$ ,

где q ₂ — заряд (с учетом знака), расположенный в точке с координатами (0; 2); r ₂ — расстояние от заряда q ₂ до начала системы координат, r ₂ = 2 м;

2) потенциал результирующего поля есть алгебраическая сумма записанных выше потенциалов

$φ = φ_{1} + φ_{2} = φ_{1} - | φ_{2} | = \frac{k q_{1}}{r_{1}} - \frac{k | q_{2} |}{r_{2}}$ .

Вычисление дает искомое значение потенциала:

$φ = \frac{9 \cdot 10^{9} \cdot 5 \cdot 10^{- 6}}{5} - \frac{9 \cdot 10^{9} \cdot 2 \cdot 10^{- 6}}{2} = 0$ В.

В начале координат потенциал результирующего поля равен нулю.

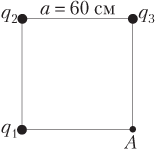
Пример 13. В трех вершинах квадрата со стороной 60 см находятся положительные заряды по 0,30 мкКл каждый. Найти потенциал результирующего поля в четвертой вершине квадрата. Диэлектрическая проницаемость среды, в которой находится система зарядов, равна единице.

Решение. На рисунке показан квадрат, в трех вершинах которого расположены одинаковые положительные заряды. Потенциал результирующего поля требуется определить в вершине A.

Рассчитаем потенциал результирующего поля в четвертой вершине квадрата, пользуясь алгоритмом:

1) потенциалы полей, образованных в точке A зарядами q ₁, q ₂ и q ₃ по отдельности, определяются следующими формулами:

поля, образованного зарядом q ₁, —

$φ_{1} = \frac{k q_{1}}{r_{1}} = \frac{k q}{a}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; q ₁ = q; r ₁ — расстояние от q ₁ до точки A, r ₁ = a;

поля, образованного зарядом q ₂, —

$φ_{2} = \frac{k q_{2}}{r_{2}} = \frac{k q}{a \sqrt{2}}$ ,

где q ₂ = q; r ₂ — расстояние от q ₂ до точки A, $r_{2} = a \sqrt{2}$ ;

поля, образованного зарядом q ₃, —

$φ_{3} = \frac{k q_{3}}{r_{3}} = \frac{k q}{a}$ ,

где q ₃ = q; r ₃ — расстояние от q ₃ до точки A, r ₃ = a;

2) потенциал результирующего поля есть алгебраическая сумма записанных выше потенциалов

$φ = φ_{1} + φ_{2} + φ_{3} = \frac{k q}{a} + \frac{k q}{a \sqrt{2}} + \frac{k q}{a} = \frac{k q}{a} (2 + \frac{1}{\sqrt{2}}) = \frac{k q}{a} \cdot \frac{4 + \sqrt{2}}{2}$ .

Вычислим:

$φ = \frac{9,0 \cdot 10^{9} \cdot 0,30 \cdot 10^{- 6}}{60 \cdot 10^{- 2}} \cdot \frac{4 + \sqrt{2}}{2} = 12 \cdot 10^{3} В = 12$ кВ.

Потенциал электростатического поля в четвертой вершине квадрата составляет 12 кВ.

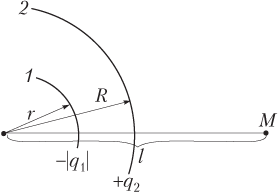
Пример 14. Две концентрические сферы радиусами 0,25 и 0,50 м заряжены равномерно зарядами –0,80 и 0,50 мкКл соответственно. Найти потенциал точки поля, расположенной на расстоянии 1,0 м от центра сфер. Система зарядов находится в вакууме.

Решение. Выполним иллюстрацию к условию задачи. Концентрические сферы имеют общий центр, сфера меньшего радиуса 1 заряжена отрицательным зарядом, а сфера большего радиуса 2 — положительным.

Потенциал электростатического поля в точке М есть алгебраическая сумма потенциалов полей, образованных первой φ₁ и второй φ₂ сферами:

φ = φ₁ + φ₂.

Рассчитаем потенциал результирующего поля, пользуясь алгоритмом:

1) потенциалы полей, образованных в точке M зарядами q ₁ и q ₂, распределенными по поверхности внутренней и внешней сферы соответственно, по отдельности определяются следующими формулами:

поля, образованного зарядом q ₁, —

$φ_{1} = \frac{k q_{1}}{r_{1}} = \frac{k q_{1}}{l}$ ,

где k — коэффициент пропорциональности, k ≈ 9 ⋅ 10⁹ Н ⋅ м²/Кл²; q ₁ — заряд, распределенный по поверхности внутренней сферы, q ₁ = −|q ₁|; r ₁ — расстояние от центра сфер до точки M, r ₁ = l;

поля, образованного зарядом q ₂, —

$φ_{2} = \frac{k q_{2}}{r_{2}} = \frac{k q_{2}}{l}$ ,

где q ₂ — заряд, распределенный по поверхности внешней сферы; r ₂ — расстояние от центра сферы до точки M, r ₂ = r ₁ = l;

2) потенциал результирующего поля есть алгебраическая сумма записанных выше потенциалов

$φ = φ_{1} + φ_{2} = \frac{k q_{1}}{l} + \frac{k q_{2}}{l} = \frac{k}{l} (q_{1} + q_{2}) = \frac{k}{l} (- | q_{1} | + q_{2})$ .

Вычислим:

$φ = \frac{9 \cdot 10^{9}}{1,0} (- 0,80 + 0,50) \cdot 10^{- 6} = - 2,7 \cdot 10^{3} В = - 2,7$ кВ.

Потенциал результирующего электростатического поля в точке М составляет −2,7 кВ. Результат не зависит от радиусов сфер.

Физика