Репетитор-онлайн — подготовка к ЦТ

7.5. Принцип суперпозиции электростатических полей

7.5.1. Принцип суперпозиции для вектора напряженности

Электростатическое поле может быть образовано не одним, а несколькими объектами. Характеристики (напряженность и потенциал) такого поля рассчитывают, используя принцип суперпозиции.

Принцип суперпозиции для напряженности позволяет рассчитать напряженность поля, образованного несколькими заряженными объектами.

Напряженность $\vec{E}$ результирующего электростатического поля, образованного несколькими зарядами в заданной точке пространства, рассчитывается как векторная сумма напряженностей полей, образованных каждым из зарядов в отдельности:

$\vec{E} = {\vec{E}}_{1} + {\vec{E}}_{2} + ... + {\vec{E}}_{n}$ ,

где ${\vec{E}}_{1}$ — напряженность поля, образованного первым зарядом; ${\vec{E}}_{2}$ — напряженность поля, образованного вторым зарядом; …; ${\vec{E}}_{n}$ — напряженность поля, образованного n-м зарядом.

Для того чтобы рассчитать напряженность поля, образованного несколькими зарядами Q ₁, Q ₂, …, Q _n в определенной точке пространства, используют следующий алгоритм:

1) на рисунке указывают направления векторов ${\vec{E}}_{1}$ , ${\vec{E}}_{2}$ , ..., ${\vec{E}}_{n}$ в заданной точке пространства с учетом знаков зарядов, их образующих;

2) записывают модули напряженностей полей, образованных каждым из зарядов Q ₁, Q ₂, …, Q _n (в отдельности):

E ₁, E ₂, …, E _n,

где E ₁ — модуль напряженности поля, образованного первым зарядом; E ₂ — модуль напряженности поля, образованного вторым зарядом; …; E _n — модуль напряженности поля, образованного n-м зарядом;

3) вводят систему координат и записывают проекции векторов ${\vec{E}}_{1}$ , ${\vec{E}}_{2}$ , ..., ${\vec{E}}_{n}$ на координатные оси:

E ₁ _x; E ₂ _x; ...; E _nx; E ₁ _y; E ₂ _y; ...; E _ny;

4) вычисляют проекции вектора напряженности результирующего поля как алгебраическую сумму записанных выше проекций:

E _x = E ₁ _x + E ₂ _x + ... + E _nx; E _y = E ₁ _y + E ₂ _y + ... + E _ny;

5) модуль напряженности результирующего поля вычисляют по формуле:

$E = \sqrt{E_{x}^{2} + E_{y}^{2}}$ .

Пример 9. Электростатическое поле образовано наложением двух однородных взаимно-перпендикулярных полей с напряженностями 300 и 400 В/м. Найти модуль напряженности результирующего поля.

Решение. Рассчитаем модуль напряженности результирующего поля, пользуясь алгоритмом:

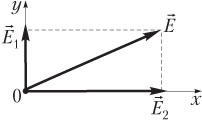
1) на рисунке показаны векторы напряженности ${\vec{E}}_{1}$ и ${\vec{E}}_{2}$ ;

2) модули векторов напряженности равны

$E_{1} = | {\vec{E}}_{1} | = 300$ В/м; $E_{2} = | {\vec{E}}_{2} | = 400$ В/м;

3) система координат показана на рисунке; проекции векторов напряженности на координатные оси равны:

E ₁ _x = 0; E ₂ _x = E ₂;

E ₁ _y = E ₁; E ₂ _y = 0;

4) проекции вектора напряженности результирующего поля рассчитаем как алгебраическую сумму записанных выше проекций:

E _x = 0 + E ₂ = E ₂; E _y = E ₁ + 0 = E ₁;

5) модуль напряженности результирующего поля найдем по формуле

$E = \sqrt{E_{x}^{2} + E_{y}^{2}} = \sqrt{E_{2}^{2} + E_{1}^{2}}$ .

Расчет дает значение:

$E = \sqrt{300^{2} + 400^{2}} = 500$ В/м.

Пример 10. В трех вершинах квадрата со стороной 25 см находятся точечные заряды по 0,25 мкКл каждый. Определить модуль напряженности электростатического поля, образованного этими зарядами в четвертой вершине квадрата.

Решение. Рассчитаем модуль напряженности результирующего поля, пользуясь алгоритмом:

1) на рисунке показаны векторы напряженности ${\vec{E}}_{1}$ , ${\vec{E}}_{2}$ и ${\vec{E}}_{3}$ полей, образованных зарядами q ₁, q ₂ и q ₃ соответственно, в четвертой вершине квадрата;

2) модули векторов напряженности определяются следующими формулами:

поля, образованного зарядом q ₁, —

$E_{1} = \frac{k q_{1}}{r_{1}^{2}} = \frac{k q}{a^{2}}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; r ₁ — расстояние между зарядом q ₁ и четвертой вершиной квадрата, r ₁ = a; q ₁ = q;

поля, образованного зарядом q ₂, —

$E_{2} = \frac{k q_{2}}{r_{2}^{2}} = \frac{k q}{2 a^{2}}$ ,

где q ₂ = q; r ₂ — расстояние между зарядом q ₂ и четвертой вершиной квадрата, $r_{2} = a \sqrt{2}$ ;

поля, образованного зарядом q ₃, —

$E_{3} = \frac{k q_{1}}{r_{3}^{2}} = \frac{k q}{a^{2}}$ ,

где q ₃ = q; r ₃ — расстояние между зарядами q ₃ и четвертой вершиной квадрата, r ₃ = a;

3) система координат показана на рисунке; проекции векторов напряженности на координатные оси равны:

E ₁ _x = E ₁; E ₂ _x = E ₂ cos 45°; E ₃ _x = 0;

E ₁ _y = 0; E ₂ _y = E ₂ sin 45°; E ₃ _x = E ₃;

4) проекции вектора напряженности результирующего поля рассчитаем как алгебраическую сумму записанных выше проекций:

$E_{x} = E_{1} + E_{2} \cos 45 ° = \frac{k q}{a^{2}} + \frac{k q}{2 a^{2}} \cos 45 ° = \frac{k q}{a^{2}} (1 + \frac{\sqrt{2}}{4})$ ;

$E_{y} = E_{2} \sin 45 ° + E_{3} = \frac{k q}{2 a^{2}} \sin 45 ° + \frac{k q}{a^{2}} = \frac{k q}{a^{2}} (1 + \frac{\sqrt{2}}{4})$ ;

5) модуль напряженности результирующего поля найдем по формуле

$E = \sqrt{E_{x}^{2} + E_{y}^{2}} = \frac{k q}{a^{2}} (1 + \frac{\sqrt{2}}{4}) \sqrt{2} = \frac{k q}{a^{2}} (\sqrt{2} + \frac{1}{2}) = \frac{k q}{a^{2}} \cdot \frac{2 \sqrt{2} + 1}{2}$ .

Вычислим:

$E = \frac{9 \cdot 10^{9} \cdot 0,25 \cdot 10^{- 6}}{{(0,25)}^{2}} \cdot \frac{2 \sqrt{2} + 1}{2} = 69 \cdot 10^{3} В/м = 69 кВ/м$ .

Величина напряженности поля в четвертой вершине квадрата составляет 69 кВ/м.

Пример 11. На двух проводящих концентрических сферах радиусами 0,25 и 0,50 м находятся заряды −0,25 и 0,55 мкКл соответственно. Определить модуль напряженности электрического поля на расстоянии 0,50 м от поверхности внешней сферы.

Решение. Выполним иллюстрацию к условию задачи. Концентрические сферы имеют общий центр, сфера меньшего радиуса 1 заряжена отрицательным зарядом, а сфера большего радиуса 2 — положительным.

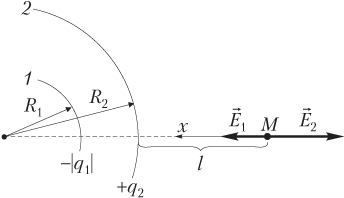
Напряженность поля в точке М есть векторная сумма напряженностей полей, образованных первой ${\vec{E}}_{1}$ и второй ${\vec{E}}_{2}$ сферами:

$\vec{E} = {\vec{E}}_{1} + {\vec{E}}_{2}$ .

Рассчитаем модуль напряженности результирующего поля, пользуясь алгоритмом:

1) на рисунке показаны векторы напряженности ${\vec{E}}_{1}$ и ${\vec{E}}_{2}$ полей, образованных зарядами q ₁ и q ₂, распределенными по поверхности внутренней и внешней сфер соответственно. Вектор ${\vec{E}}_{1}$ направлен к центру сфер, так заряд q ₁ является отрицательным, а вектор ${\vec{E}}_{2}$ — от центра сфер, так заряд q ₂ является положительным;

2) модули векторов напряженности определяются следующими формулами:

поля, образованного зарядом q ₁, —

$E_{1} = \frac{k | q_{1} |}{r_{1}^{2}} = \frac{k | q_{1} |}{{(R_{2} + l)}^{2}}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; |q ₁| — модуль заряда, распределенного по поверхности внутренней сферы; r ₁ — расстояние от центра внутренней сферы до точки M, r ₁ = R ₂ + l; R ₂ — радиус внешней сферы; l — расстояние от поверхности внешней сферы до точки M;

поля, образованного зарядом q ₂, —

$E_{2} = \frac{k q_{2}}{r_{2}^{2}} = \frac{k q_{2}}{{(R_{2} + l)}^{2}}$ ,

где q ₂ — заряд, распределенный по поверхности внешней сферы, r ₂ — расстояние от центра внешней сферы до точки M, r ₂ = r ₁ = R ₂ + l;

3) векторы напряженности направлены вдоль одной прямой в противоположные стороны; проекции векторов напряженности на координатную ось, направленную к центру сфер, равны:

E ₁ _x = E ₁; E ₂ _x = −E ₂;

4) проекция вектора напряженности результирующего поля:

$E_{x} = E_{1} - E_{2} = \frac{k | q_{1} |}{{(R_{2} + l)}^{2}} - \frac{k q_{2}}{{(R_{2} + l)}^{2}} = \frac{k}{{(R_{2} + l)}^{2}} (| q_{1} | - q_{2})$ ;

5) модуль напряженности результирующего поля найдем по формуле

$E = | E_{x} | = | E_{1} - E_{2} | = \frac{k | | q_{1} | - q_{2} |}{{(R_{2} + l)}^{2}}$ .

Вычислим:

$E = \frac{9 \cdot 10^{9} | | - 0,25 | - 0,55 | \cdot 10^{- 6}}{{(0,50 + 0,50)}^{2}} = 2,7 \cdot 10^{3} В/м = 2,7 кВ/м$ .

Величина напряженности поля в точке М составляет 2,7 кВ/м.

Физика