Физика

Напряженность и потенциал — две характеристики электростатического поля: напряженность — силовая (векторная), а потенциал — энергетическая (скалярная). Между двумя характеристиками одного и того же поля существует связь.

Однородное поле — электростатическое поле, напряженность которого в любой его точке одинакова по величине и направлению

$\overrightarrow{E}=\text{const}$.

Примерами однородных электростатических полей могут служить: поле, созданное двумя параллельными бесконечными пластинами, равномерно заряженными одинаковыми, но противоположными по знаку зарядами (поле конденсатора); поле, созданное бесконечной равномерно заряженной плоскостью.

Поле точечного заряда и поле равномерно заряженной сферы являются неоднородными, так как величина и направление вектора напряженности зависят от положения точки поля в пространстве.

Эквипотенциальная поверхность (ЭПП) — геометрическое место точек электростатического поля, в которых значения потенциала одинаковы:

φ = const.

Правила изображения электростатических полей (рис. 7.15):

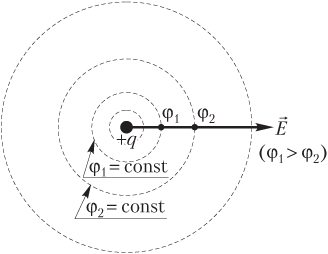
• ЭПП вокруг каждого заряда (системы зарядов) можно провести бесчисленное множество;
• для наглядности ЭПП проводят так, чтобы разности потенциалов между любыми двумя соседними поверхностями были одинаковы;
• напряженность электростатического поля имеет большее значение там, где ЭПП расположены гуще;
• линии вектора напряженности $\overrightarrow{E}$ (силовые линии) всегда перпендикулярны к эквипотенциальным поверхностям (ЭПП);
• вектор напряженности $\overrightarrow{E}$ направлен в сторону убывания потенциала.

Для однородных электростатических полей можно установить аналитическую связь между значением вектора напряженности и разностью потенциалов.

Напряженность электростатического поля характеризует изменение потенциала на единице длины. Если две точки A и B, имеющие потенциалы φ _A и φ _B соответственно, расположены:

• на разных силовых линиях (рис. 7.16), то величина напряженности и разность потенциалов связаны формулой

$E=\frac{\Delta \phi }{d}$,

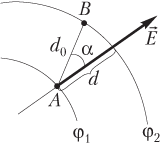
где ∆φ — разность потенциалов между точками A и B, $\Delta \phi =\left|{\phi }_B-{\phi }_A\right|$; d — расстояние между точками A и B вдоль силовой линии, на которой расположена одна из точек, d = d ₀ cos α; d ₀ — расстояние между точками A и B; α — угол между d ₀ и силовой линией $\overrightarrow{E}$;

• на одной силовой линии (рис. 7.17), то внешний вид формулы не изменятся:

$E=\frac{\Delta \phi }{d}$,

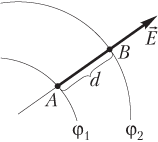
однако под величиной d подразумевают расстояние между точками A и B не вдоль силовой линии, а в пространстве (d = d ₀).