Физика
Потенциал является энергетической характеристикой электростатического поля и для данной точки пространства (занятого полем) определяется отношением энергии взаимодействия точечного электрического заряда, помещенного в данную точку, с полем к величине этого заряда:
,
где W p — энергия, которой обладает заряд q, помещенный в указанную точку поля.
Данная формула позволяет рассчитать энергию, которой обладает помещенный в поле заряд:
W p = qφ,
где φ — потенциал поля той точки пространства, в которой находится указанный заряд.
Потенциал может быть как положительным, так и отрицательным. В Международной системе единиц потенциал электростатического поля измеряется в вольтах (1 В).
Точечный заряд Q создает электростатическое поле, потенциал которого определяется формулой
,
где k — коэффициент пропорциональности (в Международной системе единиц), Н ⋅ м2/Кл2; ε0 — электрическая постоянная, ε0 = 8,85 ⋅ 10−12 Кл2/(Н ⋅ м2); ε — диэлектрическая проницаемость среды; r — расстояние между зарядом Q и той точкой поля, в которой определяется потенциал.
Потенциал поля точечного заряда является:
- положительным, если поле создается положительным зарядом Q > 0;
- отрицательным, если поле создается отрицательным зарядом Q < 0.
Сфера, равномерно заряженная зарядом Q, создает электростатическое поле, величина потенциала которого рассчитывается по-разному в разных точках пространства:
- внутри сферы и на ее поверхности потенциал поля одинаков и принимает максимальное значение, определяемое формулой
,
где k — коэффициент пропорциональности (в Международной системе единиц), Н ⋅ м2/Кл2; ε0 — электрическая постоянная, ε0 = 8,85 ⋅ 10−12 Кл2/(Н ⋅ м2); ε — диэлектрическая проницаемость среды; R — радиус сферы;
- вне сферы потенциал поля вычисляется по формуле
,
где r — расстояние от центра сферы до той точки поля, в которой определяется потенциал.
График зависимости величины потенциала от расстояния от центра сферы φ(r) изображен на рис. 7.14.
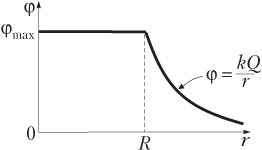
Потенциал электростатического поля заряженной сферы является:
- положительным, если поле создается положительным зарядом Q > 0;
- отрицательным, если поле создается отрицательным зарядом Q < 0.
При заземлении сферы ее потенциал обращается в нуль:
φ = 0.
Пример 8. 512 одинаковых шарообразных капелек воды заряжены до одинакового потенциала 50,0 мВ. Определить потенциал большой шарообразной капли, получившейся в результате слияния малых капель.
Решение. Сделаем иллюстрацию к условию задачи.
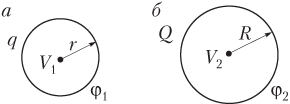
На рис. а изображена малая капля воды и введены следующие обозначения: q — заряд малой капли воды; r — радиус малой капли воды; V 1 — объем малой капли воды,
.
Потенциал электростатического поля малой капли воды определяется формулой
,
где k — коэффициент пропорциональности, k ≈ 9 ⋅ 109 Н ⋅ м2/Кл2.
На рис. б изображена большая капля воды и введены следующие обозначения: Q — заряд большой капли воды; R — радиус большой капли воды; V 2 — объем большой капли воды:
.
Потенциал электростатического поля большой капли воды определяется формулой
.
Искомое значение потенциала электростатического поля большой капли воды найдем из отношения
, т.е. .
Из закона сохранения электрического заряда следует, что отношение зарядов большой и малой капли равно
,
где n — число малых капель воды, образовавших большую каплю.
Из равенства объема большой капли воды и суммарного объема n малых капель следует, что отношение радиусов малой и большой капель равно
.
С учетом полученных выражений формула для вычисления искомого потенциала приобретает вид
,
а расчет дает его значение:
В.










