Репетитор-онлайн — подготовка к ЦТ

7.4. Характеристики электростатического поля

7.4.1. Напряженность электростатического поля

Электростатическое поле создается неподвижными зарядами. Существование в пространстве электростатического поля также определяется по наличию воздействия на электрический заряд.

Напряженность является силовой характеристикой электростатического поля и для данной точки пространства (занятого полем) определяется отношением силы, действующей на точечный электрический заряд, помещенный в эту точку поля, к величине этого заряда:

$\vec{E} = \frac{\vec{F}}{q}$ ,

где $\vec{F}$ — сила, действующая на заряд q, помещенный в указанную точку поля.

Данная формула позволяет рассчитать силу, действующую со стороны электростатического поля на помещенный в него заряд,

$\vec{F} = q \vec{E}$ .

Направление вектора напряженности электростатического поля:

совпадает с направлением силы, действующей на положительный заряд (рис. 7.4);

Рис. 7.4

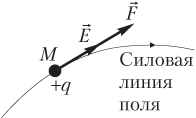
противоположно направлению силы, действующей на отрицательный заряд (рис. 7.5).

Рис. 7.5

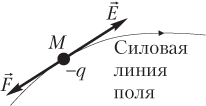
В Международной системе единиц напряженность электростатического поля измеряется в вольтах, деленных на метр (1 В/м), или в ньютонах, деленных на кулон (1 Н/Кл).

Точечный заряд Q создает электростатическое поле, модуль напряженности которого определяется формулой

$E = \frac{k | Q |}{ε r^{2}}$ ,

где k — коэффициент пропорциональности, $k = \frac{1}{4 π ε_{0}} \approx 9 \cdot 10^{9}$ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды; r — расстояние между зарядом Q и той точкой поля, в которой определяется напряженность.

Вектор напряженности электростатического поля точечного заряда $\vec{E}$ направлен:

от заряда, если поле создается положительным зарядом Q > 0 (рис. 7.6);

Рис. 7.6

к заряду, если поле создается отрицательным зарядом Q < 0 (рис. 7.7).

Рис. 7.7

Сфера, равномерно заряженная зарядом Q, создает электростатическое поле, модуль напряженности которого рассчитывается по-разному в разных точках пространства:

внутри сферы напряженность поля равна нулю:

E = 0;

на поверхности сферы модуль напряженности имеет максимальное значение и определяется формулой

$E_{\max} = \frac{k | Q |}{ε R^{2}}$ ,

где k — коэффициент пропорциональности (в Международной системе единиц), $k = \frac{1}{4 π ε_{0}} \approx 9 \cdot 10^{9}$ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды; R — радиус сферы;

вне сферы модуль напряженности поля вычисляется по формуле

$E = \frac{k | Q |}{ε r^{2}}$ ,

где r — расстояние между центром сферы и той точкой поля, в которой определяется напряженность.

График зависимости модуля напряженности от расстояния от центра сферы E(r) изображен на рис. 7.8.

Рис. 7.8

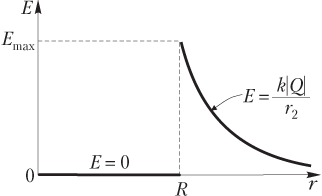
Вектор напряженности $\vec{E}$ электростатического поля направлен:

от центра сферы, если поле создается сферой, равномерно заряженной положительным зарядом Q > 0 (рис. 7.9);Рис. 7.9
к центру сферы, если поле создается сферой, равномерно заряженной отрицательным зарядом Q < 0 (рис. 7.10).Рис. 7.10

Бесконечная равномерно заряженная плоскость создает электростатическое поле, модуль напряженности которого в любой точке пространства (с каждой стороны от плоскости) одинаков и определяется формулой

$E = \frac{| σ |}{2 ε_{0} ε}$ ,

где σ — поверхностная плотность заряда; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды.

Поверхностная плотность заряда — заряд, приходящийся на единицу площади поверхности,

$σ = \frac{Q}{S}$ ,

где Q — заряд, равномерно распределенный по площади S.

В Международной системе единиц поверхностная плотность заряда измеряется в кулонах, деленных на квадратный метр (1 Кл/м²).

Вектор напряженности $\vec{E}$ электростатического поля направлен:

от плоскости, если плоскость равномерно заряжена положительным зарядом Q > 0 (рис. 7.11);

Рис. 7.11

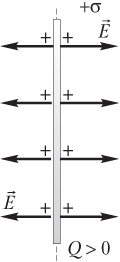
к плоскости, если плоскость равномерно заряжена отрицательным зарядом Q < 0 (рис. 7.12).

Рис. 7.12

По обе стороны от плоскости (с каждой стороны) электростатическое поле является однородным: напряженность поля $\vec{E}$ одинакова в любой точке пространства как по модулю, так и по направлению:

$\vec{E} = const$ .

Две бесконечных параллельных плоскости, равномерно заряженные одинаковыми по величине, но противоположными по знаку зарядами, создают электростатическое поле, модуль напряженности которого

в любой точке пространства между плоскостями определяется по формуле

$E = \frac{σ}{ε_{0} ε}$ ,

где σ — поверхностная плотность заряда (положительно заряженной плоскости); ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды; σ = Q/S; Q — положительный заряд, равномерно распределенный по площади S;

в остальном пространстве (снаружи от заряженных плоскостей) равна нулю:

E = 0.

Вектор напряженности $\vec{E}$ в пространстве между плоскостями направлен от положительно заряженной пластины к отрицательно заряженной пластине (рис. 7.13).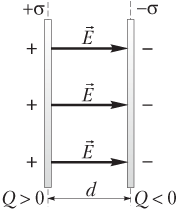Рис. 7.13

Поле во внутреннем пространстве между заряженными плоскостями является однородным (т.е. напряженность поля одинакова как по модулю, так и по направлению):

$\vec{E} = const$ .

Пример 5. Расстояние между обкладками плоского конденсатора 150 мм. На каждой из обкладок поверхностная плотность заряда одинакова и равна 800 нКл/м². Считая конденсатор воздушным, определить силу, действующую на заряд 8,85 мкКл, помещенный посередине между обкладками.

Решение. Плоский конденсатор представляет собой две разноименно заряженные пластины. Поле внутри конденсатора является однородным. Следовательно, на заряд, помещенный в любую точку пространства между обкладками конденсатора, действует одна и та же сила, модуль которой определяется формулой

F = qE,

где q — величина заряда; E — напряженность электрического поля конденсатора.

В пространстве между пластинами плоского конденсатора модуль напряженности поля может быть рассчитан с помощью выражения

$E = \frac{σ}{ε ε_{0}}$ ,

где σ — поверхностная плотность заряда; ε — диэлектрическая проницаемость воздуха, ε = 1; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²).

Подставив выражение для модуля напряженности электростатического поля в формулу для силы, получим

$F = \frac{q σ}{ε ε_{0}}$ .

Вычислим:

$F = \frac{8,85 \cdot 10^{- 6} \cdot 800 \cdot 10^{- 9}}{8,85 \cdot 10^{- 12}} = 800 \cdot 10^{- 3} Н = 800$ мН.

На заряд, помещенный между обкладками плоского воздушного конденсатора, в любой точке пространства действует сила 800 мН. Следует заметить, что результат не зависит от положения заряда между обкладками конденсатора.

Пример 6. Капля росы в форме шара получилась в результате слияния 125 одинаковых заряженных капелек тумана. Во сколько раз напряженности поля на поверхности капли росы больше напряженности на поверхности капельки тумана?

Решение. Сделаем иллюстрацию к условию задачи.

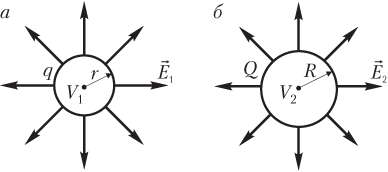
Капелька тумана изображена на рис. а и введены следующие обозначения: q — заряд капельки тумана; r — радиус капельки тумана; V ₁ — объем капельки тумана,

$V_{1} = \frac{4}{3} π r^{3}$ .

Напряженность электростатического поля на поверхности капельки тумана определяется формулой

$E_{1} = \frac{k q}{r^{2}}$ ,

где k — коэффициент пропорциональности, k = 9 ⋅ 10⁹ Н ⋅ м²/Кл².

Капля росы изображена на рис. б и введены следующие обозначения: Q — заряд капли росы; R — радиус капли росы; V ₂ — объем капли росы,

$V_{2} = \frac{4}{3} π R^{3}$ .

Напряженность электростатического поля на поверхности капли росы определяется формулой

$E_{2} = \frac{k Q}{R^{2}}$ .

Искомым является отношение

$\frac{E_{2}}{E_{1}} = \frac{Q}{q} \cdot {(\frac{r}{R})}^{2}$ .

Согласно закону сохранения электрического заряда, заряд капли росы равен суммарному заряду капелек тумана:

Q = nq,

где n — число капелек тумана, образовавших каплю росы.

При слиянии указанного количества капелек тумана в каплю росы, объемы капелек тумана складываются. Отношение радиусов капельки тумана и капли росы найдем из равенства

V ₂ = nV ₁.

Подставляя выражения для V ₁ и V ₂ в записанное соотношение между объемами, получим

$\frac{4}{3} π R^{3} = n \frac{4}{3} π r^{3}$ .

Отсюда следует, что

$\frac{r}{R} = \frac{1}{\sqrt[3]{n}}$ .

С учетом полученных выражений искомое отношение напряженностей приобретает вид

$\frac{E_{2}}{E_{1}} = \frac{Q}{q} \cdot {(\frac{r}{R})}^{2} = \frac{n}{{(\sqrt[3]{n})}^{2}} = \sqrt[3]{n}$ .

Расчет дает значение

$\frac{E_{2}}{E_{1}} = \sqrt[3]{125} = 5$ .

Напряженность электростатического поля на поверхности капли росы в 5 раз больше напряженности поля на поверхности капельки тумана.

Пример 7. Электрическое поле создано электрическим зарядом 5,0 мкКл, расположенным в начале координат плоскости xOy, где x и y заданы в метрах. Определить модуль напряженности электростатического поля в точке с координатами (3,0; 4,0), считая, что заряд находится в вакууме.

Решение. На рисунке представлена система координат xOy, в начале которой расположен заряд Q, создающий электростатическое поле в окружающем его пространстве, и точка M, в которой требуется определить величину напряженности поля этого заряда.

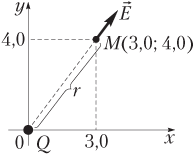
Заряд, образующий поле, является точечным, поэтому модуль напряженности электростатического поля рассчитаем по формуле

$E = \frac{k Q}{r^{2}}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; r — расстояние между зарядом Q и точкой пространства с указанными координатами, $r = \sqrt{{(3,0)}^{2} + {(4,0)}^{2}} = 5,0$ м.

Вычислим:

$E = \frac{9,0 \cdot 10^{9} \cdot 5,0 \cdot 10^{- 6}}{{5,0}^{2}} = 1,8 \cdot 10^{3} В/м = 1,8 кВ/м$ .

Физика