Репетитор-онлайн — подготовка к ЦТ

7.3. Взаимодействие зарядов

7.3.2. Взаимодействие нескольких зарядов

Закон Кулона позволяет рассчитать силу взаимодействия нескольких зарядов.

Сила, с которой на заряд Q действуют n точечных зарядов (q ₁, q ₂, …, q _n), определяется суммой (рис. 7.3)

$\vec{F} = {\vec{F}}_{1} + {\vec{F}}_{2} + ... + {\vec{F}}_{n}$ ,

где ${\vec{F}}_{1}$ — сила взаимодействия заряда Q с зарядом q ₁; ${\vec{F}}_{2}$ — сила взаимодействия заряда Q с зарядом q ₂; …; ${\vec{F}}_{n}$ — сила взаимодействия заряда Q с зарядом q _n.

Для вычисления модуля равнодействующей силы $\vec{F}$ используют следующий алгоритм:

1) на рисунке показывают все силы, действующие на заряд Q со стороны каждого из зарядов q ₁, q ₂, …, q _n в отдельности (с учетом знаков взаимодействующих зарядов);

Рис. 7.3

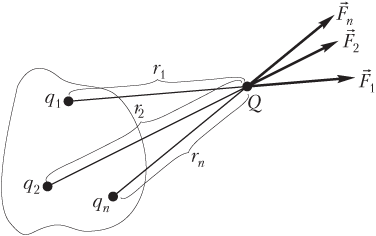
2) записывают модули сил взаимодействия заряда Q с каждым из зарядов q ₁, q ₂, …, q _n в отдельности:

$F_{1} = \frac{k | q_{1} Q |}{ε r_{1}^{2}}$ , $F_{2} = \frac{k | q_{2} Q |}{ε r_{2}^{2}}$ , …, $F_{n} = \frac{k | q_{n} Q |}{ε r_{n}^{2}}$ ,

где k — коэффициент пропорциональности, $k = \frac{1}{4 π ε_{0}} \approx 9 \cdot 10^{9}$ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/Н ⋅ м²; ε — диэлектрическая проницаемость среды, в которой находятся заряды; r ₁ — расстояние между зарядами Q и q ₁; r ₂ — расстояние между зарядами Q и q ₂; …; r _n — расстояние между зарядами Q и q _n;

3) вводят систему координат и записывают проекции всех сил на координатные оси:

F ₁ _x; F ₂ _x; ...; F _nx;

F ₁ _y; F ₂ _y; ...; F _ny;

4) вычисляют проекции равнодействующей как алгебраическую сумму проекций сил:

F _x = F ₁ _x + F ₂ _x + ... + F _nx;

F _y = F ₁ _y + F ₂ _y + ... + F _ny;

5) модуль равнодействующей вычисляют по формуле

$F = \sqrt{F_{x}^{2} + F_{y}^{2}}$ .

Пример 3. В трех вершинах квадрата со стороной 50 см находятся заряды по 1,0 мкКл. Определить силу, действующую на заряд 0,10 мКл, помещенный в четвертую вершину квадрата. Система зарядов находится в вакууме.

Решение. Выполним рисунок, на котором покажем силы взаимодействия заряда Q = 0,10 мКл с каждым из зарядов q ₁ = q ₂ = q ₃ = q = 1,0 мкКл.

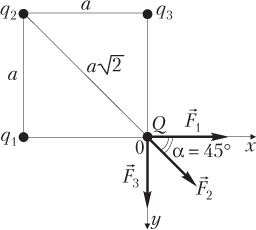
Согласно алгоритму:

1) модули сил взаимодействия зарядов q ₁, q ₂ и q ₃ с зарядом Q могут быть рассчитаны по формулам

$F_{1} = \frac{k q_{1} Q}{r_{1}^{2}} = \frac{k q Q}{a^{2}}$ ;

$F_{2} = \frac{k q_{2} Q}{r_{2}^{2}} = \frac{k q Q}{2 a^{2}}$ ;

$F_{3} = \frac{k q_{3} Q}{r_{3}^{2}} = \frac{k q Q}{a^{2}}$ ,

где k — коэффициент пропорциональности в законе Кулона, k = = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; r ₁ — расстояние между зарядами q ₁ и Q; r ₂ — расстояние между зарядами q ₂ и Q; r ₃ — расстояние между зарядами q ₃ и Q; r ₁ = r ₃ = a, $r_{2} = a \sqrt{2}$ ; a — сторона квадрата;

2) проекции сил ${\vec{F}}_{1}$ , ${\vec{F}}_{2}$ и ${\vec{F}}_{3}$ на оси системы координат:

$F_{1 x} = F_{1} = \frac{k q Q}{a^{2}}$ ; $F_{2 x} = F_{2} \cos 45 ° = \frac{k q Q}{2 a^{2}} \cdot \frac{\sqrt{2}}{2}$ ; F ₃ _x = 0;

F ₁ _y = 0; $F_{2 y} = F_{2} \sin 45 ° = \frac{k q Q}{2 a^{2}} \cdot \frac{\sqrt{2}}{2}$ ; $F_{3 y} = F_{3} = \frac{k q Q}{a^{2}}$ ;

3) проекции результирующей силы на координатные оси:

$F_{x} = F_{1 x} + F_{2 x} + F_{3 x} = \frac{k q Q}{2 a^{2}} (1 + \frac{\sqrt{2}}{4})$ ;

$F_{y} = F_{1 y} + F_{2 y} + F_{3 y} = \frac{k q Q}{a^{2}} (1 + \frac{\sqrt{2}}{4})$ ;

4) модуль искомой силы:

$F = \sqrt{F_{x}^{2} + F_{y}^{2}} = \sqrt{2} \frac{k q Q}{a^{2}} (1 + \frac{\sqrt{2}}{4}) = \frac{k q Q}{a^{2}} (\sqrt{2} + 0,5)$ .

Вычислим:

$F = \frac{9,0 \cdot 10^{9} \cdot 1,0 \cdot 10^{- 6} \cdot 0,10 \cdot 10^{- 3}}{50^{2} \cdot 10^{- 4}} (\sqrt{2} + 0,5) = 6,9$ Н.

Пример 4. Три одинаковых положительных точечных заряда величиной по $\sqrt{3}$ мкКл расположены в вершинах равностороннего треугольника, находящегося в вакууме. Какой заряд нужно поместить в центр этого треугольника, чтобы вся система находилась в равновесии?

Решение. Выполним рисунок, иллюстрирующий условие задачи, на котором покажем силы взаимодействия заряда, расположенного в одной из вершин треугольника с остальными зарядами.

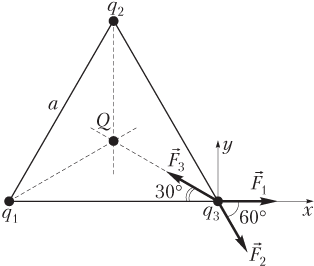
Величина и знак заряда Q, помещенного в центр треугольника, должны обеспечивать равновесие системы зарядов, т.е. должно выполняться условие равновесия

${\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{3} = 0$ ,

где ${\vec{F}}_{1}$ — сила взаимодействия заряда q ₃ с зарядом q ₁; ${\vec{F}}_{2}$ — сила взаимодействия заряда q ₃ с зарядом q ₂; ${\vec{F}}_{3}$ — сила взаимодействия заряда q ₃ с зарядом Q; заряд Q должен иметь отрицательный знак, а соответствующая сила должна быть силой притяжения.

Модули указанных сил взаимодействия зарядов системы имеют следующий вид:

силы взаимодействия заряда q ₃ с зарядом q ₁ –

$F_{1} = \frac{k q_{1} q_{3}}{r_{1}^{2}} = \frac{k q^{2}}{a^{2}}$ ,

где k — коэффициент пропорциональности в законе Кулона, k = = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; q ₁ = q ₃ = q; r ₁ — расстояние между зарядами q ₁ и q ₂, r ₁ = a; a — сторона треугольника;

силы взаимодействия заряда q ₃ с зарядом q ₂ —

$F_{2} = \frac{k q_{2} q_{3}}{r_{2}^{2}} = \frac{k q^{2}}{a^{2}}$ ,

где q ₂ = q ₃ = q; r ₂ — расстояние между зарядами q ₂ и q ₃, r ₂ = a;

силы взаимодействия заряда q ₃ с зарядом Q —

$F_{3} = \frac{k q_{1} | Q |}{r_{3}^{2}} = \frac{3 k q | Q |}{a^{2}}$ ,

где q ₃ = q; r ₃ — расстояние между зарядами q ₃ и Q, $r_{3} = a / \sqrt{3}$ .

Проекции указанных сил на координатные оси определяются выражениями:

$F_{1 x} = F_{1} = \frac{k q^{2}}{a^{2}}$ ;

$F_{2 x} = F_{2} \cos 60 ° = \frac{k q^{2}}{2 a^{2}}$ ;

$F_{3 x} = - F_{3} \cos 30 ° = - \frac{3 \sqrt{3} k q | Q |}{2 a^{2}}$ ;

F ₁ _y = 0;

$F_{2 y} = - F_{2} \sin 60 ° = - \frac{\sqrt{3} k q^{2}}{2 a^{2}}$ ;

$F_{3 y} = F_{3} \sin 30 ° = \frac{3 k q | Q |}{2 a^{2}}$ .

Условие равновесия в проекциях на координатные оси принимает вид $\begin{array}{l} F_{1 x} + F_{2 x} + F_{3 x} = 0, \\ F_{1 y} + F_{2 y} + F_{3 y} = 0, \end{array}}$

или $\begin{array}{l} \frac{k q^{2}}{a^{2}} + \frac{k q^{2}}{2 a^{2}} - \frac{3 \sqrt{3} k q | Q |}{2 a^{2}} = 0, \\ - \frac{\sqrt{3} k q^{2}}{2 a^{2}} + \frac{3 k q | Q |}{2 a^{2}} = 0. \end{array}}$

Уравнения системы одинаковы; решение одного из них относительно |Q| дает результат

$| Q | = \frac{q}{\sqrt{3}} = \frac{q \sqrt{3}}{3} = \frac{\sqrt{3 \cdot} 10^{- 6} \cdot \sqrt{3}}{3} = 1 \cdot 10^{- 6} Кл = 1$ мкКл.

Для того чтобы система зарядов находилась в равновесии, в центр треугольника следует поместить отрицательный заряд (−1 мкКл).

Физика