Репетитор-онлайн — подготовка к ЦТ

7.3. Взаимодействие зарядов

7.3.1. Взаимодействие двух зарядов (закон Кулона)

Два неподвижных точечных заряда q ₁ и q ₂ действуют друг на друга с силой, модуль которой вычисляется по закону Кулона:

$F = \frac{k | q_{1} q_{2} |}{ε r^{2}}$ ,

где k — коэффициент пропорциональности (в Международной системе единиц), $k = \frac{1}{4 π ε_{0}} = 9,0 \cdot 10^{9}$ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/(Н ⋅ м²); ε — диэлектрическая проницаемость среды, в которой находятся заряды; r — расстояние между точечными зарядами.

Закон Кулона также можно применять для расчета силы взаимодействия двух заряженных тел сферической формы; в этом случае r — расстояние между центрами сфер (шаров).

Силы Кулона, действующие на каждый из взаимодействующих зарядов, равны по модулю, противоположны по направлению и приложены к разным зарядам:

${\vec{F}}_{1} = - {\vec{F}}_{2}$ ,

где ${\vec{F}}_{1}$ — сила, действующая на заряд q ₁; ${\vec{F}}_{2}$ — сила, действующая на заряд q ₂.

Сила Кулона, направленная по линии, соединяющей заряды, является:

силой отталкивания (рис. 7.1), если заряды q ₁ и q ₂ — одноименные (имеют одинаковый знак);

Рис. 7.1

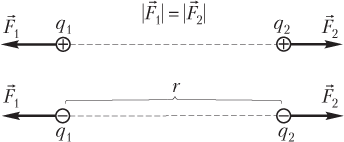
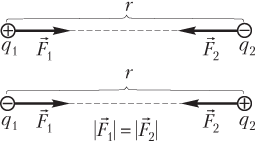
силой притяжения (рис. 7.2), если заряды q ₁ и q ₂ — разноименные (имеют разные знаки).

Рис. 7.2

Для зарядов, находящихся в вакууме (воздухе), закон Кулона принимает вид

$F = \frac{k | q_{1} q_{2} |}{r^{2}}$ ,

где k — коэффициент пропорциональности (в Международной системе единиц), $k = \frac{1}{4 π ε_{0}} \approx 9 \cdot 10^{9}$ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Кл²/Н ⋅ м²; q ₁, q ₂ — взаимодействующие заряды; r — расстояние между зарядами.

Диэлектрическая проницаемость вакуума (воздуха) считается равной единице: ε = 1.

Пример 1. Во сколько раз уменьшится сила взаимодействия двух одинаковых точечных зарядов, если каждый из них уменьшить в 4,0 раза и перенести из вакуума в среду с диэлектрической проницаемостью, равной 2,5? Расстояние между зарядами не изменяется.

Решение. Запишем дважды закон Кулона:

для зарядов q ₁ = q ₂ = q, находящихся в вакууме, —

$F_{1} = \frac{k q^{2}}{r^{2}}$ ,

где k — коэффициент пропорциональности, k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; r — расстояние между зарядами;

для зарядов ${q^{'}}_{1} = {q^{'}}_{2} = q^{'} = q / 4$ , находящихся в среде с диэлектрической проницаемостью ε = 2,5, —

$F_{2} = \frac{k {(q^{'})}^{2}}{ε r^{2}}$ .

Отношение сил (F ₁/F ₂) является искомым и определяется формулой

$\frac{F_{1}}{F_{2}} = \frac{q^{2} ε}{{(q^{'})}^{2}} = \frac{16 q^{2} ε}{q^{2}} = 16 ε$ .

Расчет дает значение

$\frac{F_{1}}{F_{2}} = 16 \cdot 2,5 = 40$ .

Следовательно, сила кулоновского взаимодействия уменьшится в 40 раз.

Пример 2. Два одинаковых шарика, заряженных одинаковыми зарядами, подвешены на длинных непроводящих нитях одинаковой длины и находятся в керосине. Плотность керосина равна 0,80 г/см³, а плотность материала, из которого изготовлены шарики, — 1,6 г/см³. Определить относительную диэлектрическую проницаемость керосина, если в воздухе нити расходятся на такой же угол, как и в керосине.

Решение. Проиллюстрируем условие задачи рисунками. На рисунках показаны силы, действующие на один из шариков в керосине (рис. а) и в воздухе (рис. б).

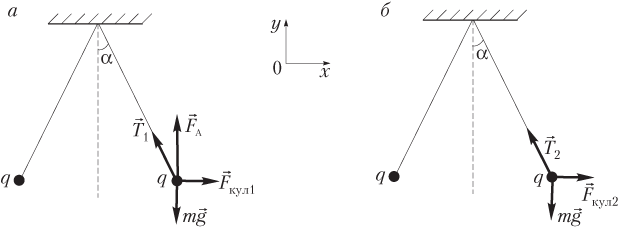
Условия равновесия шариков имеют следующий вид:

в керосине —

$m \vec{g} + {\vec{T}}_{1} + {\vec{F}}_{A} + {\vec{F}}_{кул 1} = 0$ ,

где $m \vec{g}$ — сила притяжения шарика к Земле; ${\vec{T}}_{1}$ — сила натяжения нити в керосине; ${\vec{F}}_{A}$ — сила Архимеда; ${\vec{F}}_{кул 1}$ — кулоновская сила, действующая на шарик в керосине;

в воздухе —

$m \vec{g} + {\vec{T}}_{2} + {\vec{F}}_{кул 2} = 0$ ,

где ${\vec{T}}_{2}$ — сила натяжения нити в воздухе; ${\vec{F}}_{кул 2}$ — кулоновская сила, действующая на шарик в воздухе.

Условия равновесия в проекциях на координатные оси образуют систему уравнений:

$\begin{array}{l} F_{кул 1} - T_{1} \sin (α / 2) = 0, \\ F_{кул 2} - T_{2} \sin (α / 2) = 0, \\ F_{A} + T_{1} \cos (α / 2) - m g = 0, \\ T_{2} \cos (α / 2) - m g = 0, \end{array}}$

где F _кул1 — сила кулоновского взаимодействия зарядов, находящихся в керосине, $F_{кул 1} = k q^{2} / ε r^{2}$ ; k — коэффициент пропорциональности, k ≈ 9 ⋅ 10⁹ Н ⋅ м²/Кл²; q — величина каждого из зарядов; ε — диэлектрическая проницаемость керосина; r — расстояние между зарядами; F _кул2 — сила кулоновского взаимодействия зарядов, находящихся в воздухе, $F_{кул 2} = k q^{2} / r^{2}$ ; F _A — сила Архимеда, действующая на каждый из шариков в керосине, F _A = ρ_кgV; ρ_к — плотность керосина; g — модуль ускорения свободного падения; V — объем каждого из шариков; m — масса каждого из шариков; α — угол, на который разошлись шарики.

Исключим из системы силы натяжения нити. Для этого преобразуем систему к виду

$\begin{array}{l} T_{1} \sin (α / 2) = F_{кул 1}, \\ T_{2} \sin (α / 2) = F_{кул 2}, \\ T_{1} \cos (α / 2) = m g - F_{A}, \\ T_{2} \cos (α / 2) = m g \end{array}}$

и попарно разделим уравнения

$\begin{array}{l} \frac{T_{1}}{T_{2}} = \frac{F_{кул 1}}{F_{кул 2}}, \\ \frac{T_{1}}{T_{2}} = \frac{m g - F_{A}}{m g} . \end{array}}$

Равенство правых частей уравнений, записанное с учетом явных выражений кулоновских сил и силы Архимеда, т.е.

$\frac{1}{ε} = \frac{m - ρ_{к} V}{m}$ ,

позволяет найти диэлектрическую проницаемость керосина:

$ε = \frac{m}{m - ρ_{к} V}$ .

Выразив массу шарика через плотность материала, из которого он изготовлен, и его объем (m = ρV), получим формулу для искомой величины и рассчитаем:

$ε = \frac{ρ}{ρ - ρ_{к}} = \frac{1,6 \cdot 10^{3}}{1,6 \cdot 10^{3} - 0,80 \cdot 10^{3}} = 2,0$ .

Керосин обладает диэлектрической проницаемостью, равной 2,0.

Физика