Физика
Решая задачи о связанных телах, рекомендуется записывать второй закон Ньютона для каждого тела в отдельности.
Два тела, связанные нерастяжимой нитью, движутся с одинаковым (по величине) ускорением (рис. 2.22):
a1 = a2,
где a1 — модуль ускорения первого тела; a2 — модуль ускорения второго тела.
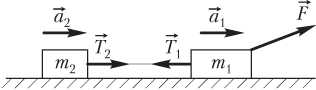
На каждое из двух тел, связанных невесомой нитью, со стороны нити действует одинаковая (по величине) сила реакции (натяжения) нити:
T1 = T2,
где T1 — модуль силы реакции (натяжения) нити, действующей на первое тело; T2 — модуль силы реакции (натяжения) нити, действующей на второе тело.
Если тела связаны невесомой нерастяжимой нитью, перекинутой через блок, то натяжение нити будет одинаковым по обе стороны от блока в том случае, когда блок считается невесомым и трением в его оси можно пренебречь (рис. 2.23).
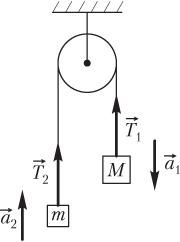
Задачу о взаимодействующих телах (или о взаимодействующих частях одного тела) рекомендуется сводить к задаче о связанных телах.
Пример 29. Два тела, связанные невесомой нерастяжимой нитью, движутся по горизонтальной поверхности под действием силы, численно равной и приложенной под углом 30° к горизонту к одному из тел. Определить модуль силы натяжения нити, если коэффициент трения между телами и поверхностью равен 0,8. Масса тела, к которому приложена сила, равна 0,8 кг, масса второго тела — 1,2 кг.
Решение. Силы, действующие на тела, показаны на рисунке.
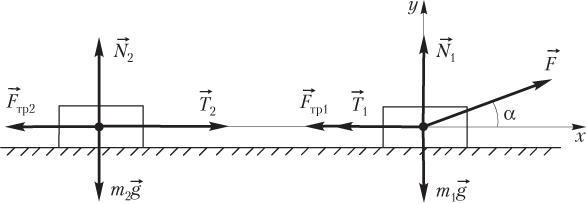
Запишем второй закон Ньютона:
- для первого тела —
,
или в проекциях на координатные оси
где m 1 — масса первого тела; a 1 — модуль ускорения первого тела; g — модуль ускорения свободного падения; N 1 — модуль силы нормальной реакции опоры, действующей на первое тело; F тр1 — модуль силы трения, действующей на первое тело; F — модуль силы, приложенной к первому телу под углом α к горизонту; T 1 — модуль силы натяжения нити, действующей на первое тело;
- для второго тела —
,
или в проекциях на координатные оси
где m 2 — масса второго тела; a 2 — модуль ускорения второго тела; N 2 — модуль силы нормальной реакции опоры, действующей на второе тело; F тр2 — модуль силы трения, действующей на второе тело; T 2 — модуль силы натяжения нити, действующей на второе тело.
С учетом
- выражений для сил трения
F тр1 = µN 1,
F тр2 = µN 2;
- условия невесомости нити
T 1 = T 2 = T;
- условия нерастяжимости нити
a 1 = a 2 = a
составим полную систему уравнений:
Из второго и четвертого уравнений системы выразим силы нормальной реакции опоры, действующие на первое и второе тела:
N 1 = m 1g − F sin α,
N 2 = m 2g.
Полученные выражения подставим в первое и третье уравнения:
Система содержит два неизвестных: a и T. Величина силы натяжения нити T является искомой.
Деление уравнений
и последующие преобразования данного отношения позволяют получить формулу для вычисления силы натяжения нити:
.
Произведем расчет:
Н.
Пример 30. Два тела, связанные нитью, перекинутой через невесомый блок, закреплены на вершине наклонной плоскости с углом 45° при основании. На наклонной плоскости находится тело массой 1,5 кг, масса свешивающегося тела равна 6,0 кг. Определить модуль силы натяжения нити, если коэффициент трения между первым телом и плоскостью равен 0,5. Трением в оси блока пренебречь.
Решение. Силы, действующие на тела, и оси системы координат, выбранные для каждого тела, показаны на рисунке.
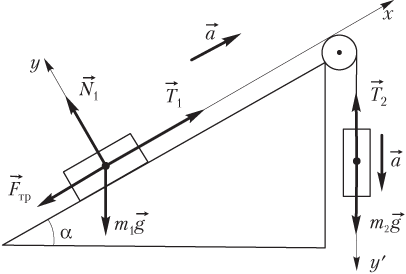
Запишем второй закон Ньютона:
- для тела, находящегося на наклонной плоскости —
,
или в проекциях на координатные оси
где m 1 — масса тела, находящегося на наклонной плоскости; a 1 — модуль ускорения тела, находящегося на наклонной плоскости; g — модуль ускорения свободного падения; N — модуль силы нормальной реакции наклонной плоскости; F тр = µN — модуль силы трения, действующей на тело со стороны наклонной плоскости; µ — коэффициент трения; T 1 — модуль силы натяжения нити, действующей на тело, находящееся на наклонной плоскости; α — угол наклона плоскости к горизонту;
- для свешивающегося тела —
,
или в проекции на координатную ось Oy′:
,
где m 2 — масса свешивающегося тела; a 2 — модуль ускорения свешивающегося тела; T 2 — модуль силы натяжения нити, действующей на свешивающееся тело.
С учетом
- выражения для силы трения
F тр = µN;
- условия невесомости нити
T 1 = T 2 = T;
- условия нерастяжимости нити
a 1 = a 2 = a
составим полную систему уравнений:
Из второго уравнения системы следует, что модуль силы нормальной реакции опоры, действующей на тело со стороны наклонной плоскости, определяется формулой
N = m 1g cos α.
Подстановка полученного выражения в первое уравнение системы приводит ее к следующему виду:
Система содержит два неизвестных: a и T. Величина силы натяжения нити T является искомой.
Деление уравнений
и последующие преобразования данного отношения позволяют получить формулу для вычисления величины силы натяжения нити:
.
Произведем расчет:
Н.
Пример 31. К грузу массой 12 кг прикреплен груз массой 3,0 кг. Крепление произведено при помощи однородной веревки массой 6,0 кг. Определить модуль силы натяжения веревки в точке, расположенной на расстоянии 1/3 ее длины от первого груза, если систему поднимают вверх с ускорением 2,0 м/с2.
Решение. Для решения задачи целесообразно использовать следующую модель (рисунок иллюстрирует ее применение):
1) веревка заменяется на невесомую;
2) одна треть массы веревки m 0 прибавляется к массе первого груза m 1:
;
3) две трети массы веревки m 0 прибавляются к массе второго груза m 2:
.
Далее решение задачи является традиционным.
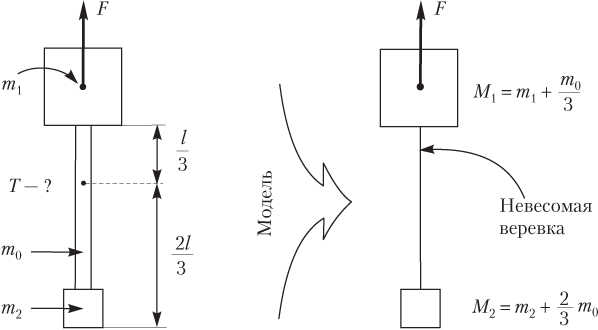
На рисунке изображены тела массами M 1 и M 2, связанные невесомой нерастяжимой нитью.
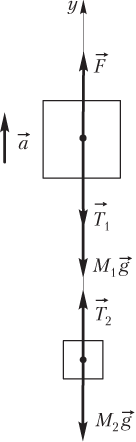
Запишем второй закон Ньютона:
- для первого тела —
,
или в проекции на координатную ось Oy
,
где — суммарная масса первого тела и одной трети веревки; a 1 — модуль ускорения тела массой M 1; g — модуль ускорения свободного падения; F — модуль силы, приложенной к первому телу; T 1 — модуль силы натяжения нити, действующей на тело массой M 1;
- для второго тела —
,
или в проекции на координатную ось Oy
T 2 − M 2g = M 2a 2,
где — суммарная масса второго тела и двух третей веревки; a 2 — модуль ускорения тела массой M 2; T 2 — модуль силы натяжения нити, действующей на тело массой M 2.
С учетом
- условия невесомости нити
T 1 = T 2 = T;
- условия нерастяжимости нити
a 1 = a 2 = a
составим полную систему уравнений:
Второе уравнение позволяет найти величину искомой силы натяжения нити:
Н.
Пример 32. На горизонтальной поверхности лежат вплотную два одинаковых кубика массой по 200 г. К первому кубику приложена горизонтальная сила 10,0 Н, действующая в направлении второго кубика. Коэффициент трения между первым кубиком и поверхностью равен 0,2, между вторым и поверхностью — 0,3. Определить модуль результирующей силы, действующей на второй кубик.
Решение. Рассмотрим взаимодействующие кубики, используя модель связанных тел. На рисунке показаны связанные (взаимодействующие) кубики.
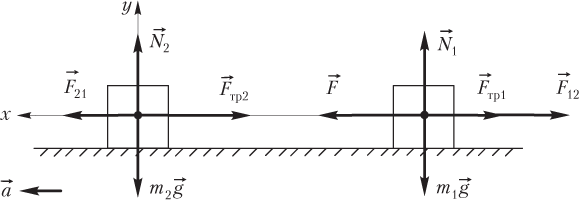
Первый кубик действует на второй с силой , а второй на первый — с силой . Согласно третьему закону Ньютона, эти силы равны между собой по величине и противоположны по направлению:
.
Запишем второй закон Ньютона:
- для первого кубика —
,
или в проекциях на координатные оси
где m 1 — масса первого кубика; a 1 — модуль ускорения первого кубика; g — модуль ускорения свободного падения; N 1 — модуль силы нормальной реакции опоры, действующей на первый кубик; F тр1 — модуль силы трения, действующей на первый кубик; F — модуль силы, приложенной к первому кубику; F 12 — модуль силы, действующей на первый кубик со стороны второго;
- для второго кубика —
,
или в проекциях на координатные оси
где m 2 — масса второго кубика; a 2 — модуль ускорения второго кубика; N 2 — модуль силы нормальной реакции опоры, действующей на второй кубик; F тр2 — модуль силы трения, действующей на второй кубик; F 21 — модуль силы, действующей на второй кубик со стороны первого.
Левая часть уравнения, выражающего второй закон Ньютона, представляет собой искомую результирующую силу, действующую на второй кубик:
.
Следовательно, искомой величиной может считаться произведение
,
представляющее собой правую часть указаного уравнения.
С учетом
- выражений для сил трения
F тр1 = µ1N 1,
F тр2 = µ2N 2;
- равенства модулей сил взаимодействия
F вз = F 12 = F 21;
- равенства модулей ускорений взаимодействующих тел
a 1 = a 2 = a;
- равенства масс кубиков
m 1 = m 2 = m
составим полную систему уравнений:
где µ1 — коэффициент трения между первым кубиком и плоскостью; µ2 — коэффициент трения между вторым кубиком и плоскостью.
Из второго и четвертого уравнений системы выразим силы нормальной реакции опоры, действующие на первый и второй кубики:
N 1 = mg,
N 2 = mg.
Полученные выражения подставим в первое и третье уравнения:
Система содержит два неизвестных: a и F вз. Для нахождения результирующей силы, действующей на второй кубик, целесообразно найти модуль ускорения a.
Суммирование уравнений
и последующие преобразования позволяют получить формулы для вычисления величины ускорения:
и для модуля результирующей силы, действующей на второй кубик:
.
Выполним вычисление:
Н.
Решение данной задачи можно существенно упростить, если записать второй закон Ньютона для системы, состоящей из двух кубиков, и рассмотреть ее движение как целого. Однако при таком решении силы взаимодействия между телами остаются вне поля зрения.
Пример 33. Два бруска одинаковой массы по 0,4 кг поставили на наклонную плоскость с углом наклона 60° так, чтобы они соприкасались друг с другом. Коэффициент трения верхнего бруска о плоскость равен 0,2, нижнего — 0,8. Определить силу взаимодействия брусков.
Решение. Рассмотрим взаимодействующие бруски, используя модель связанных тел. На рисунке показаны связанные (взаимодействующие) бруски.
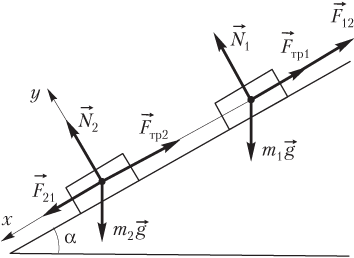
Верхний брусок действует на нижний с силой , а нижний на верхний — с силой . Согласно третьему закону Ньютона, эти силы равны между собой по величине и противоположны по направлению:
.
Запишем второй закон Ньютона:
- для верхнего бруска —
,
или в проекциях на координатные оси
где m 1 — масса верхнего бруска; a 1 — модуль ускорения верхнего бруска; g — модуль ускорения свободного падения; N 1 — модуль силы нормальной реакции наклонной плоскости, действующей на верхний брусок; F тр1 — модуль силы трения, действующей на верхний брусок; F 12 — модуль силы, действующей на верхний брусок со стороны нижнего; α — угол наклона плоскости к горизонту;
- для нижнего бруска —
,
или в проекциях на координатные оси
где m 2 — масса нижнего бруска; a 2 — модуль ускорения нижнего бруска; N 2 — модуль силы нормальной реакции наклонной плоскости, действующей на нижний брусок; F тр2 — модуль силы трения, действующей на нижний брусок; F 21 — модуль силы, действующей на нижний брусок со стороны верхнего.
С учетом
- выражений для сил трения
F тр1 = µ1N 1,
F тр2 = µ2N 2;
- равенства модулей сил взаимодействия
F вз = F 12 = F 21;
- равенства модулей ускорений взаимодействующих тел
a 1 = a 2 = a;
- равенства масс брусков
m 1 = m 2 = m
составим полную систему уравнений:
где µ1 — коэффициент трения между верхним бруском и наклонной плоскостью; µ2 — коэффициент трения между нижним бруском и наклонной плоскостью.
Из второго и четвертого уравнений системы выразим силы реакции наклонной плоскости, действующие на верхний и нижний бруски:
N 1 = mg cos α,
N 2 = mg cos α.
Полученные выражения подставим в первое и третье уравнения:
Система содержит два неизвестных: a и F вз. Величина силы взаимодействия между брусками F вз является искомой.
Равенство правых частей уравнений системы позволяет записать равенство их левых частей:
.
Преобразования данного выражения позволяют получить формулу для вычисления величины силы взаимодействия между брусками:
.
Произведем расчет:
Н.










