Репетитор-онлайн — подготовка к ЦТ

2.4. Основные законы классической динамики

2.4.2. Применение второго закона Ньютона к решению задач о движении одного тела

Второй закон Ньютона по праву считается основным законом динамики.

Ускорение $\vec{a}$ , приобретаемое материальной точкой, пропорционально равнодействующей всех сил $\vec{F}$ и обратно пропорционально массе m материальной точки (второй закон Ньютона):

$\vec{a} = \frac{\vec{F}}{m}$ .

Направление ускорения совпадает с направлением действия равнодействующей сил, приложенных к телу.

При поступательном движении материальной точки (тела) с постоянной скоростью $(\vec{a} = 0)$ равнодействующая сил равна нулю (рис. 2.19):

$\vec{F} = 0$ ,

т.е. проекции равнодействующей на координатные оси равны нулю:

F ₁ _x + F ₂ _x + ... + F _Nx = 0;

F ₁ _y + F ₂ _y + ... + F _Ny = 0,

где F ₁ _x, F ₂ _x, ..., F _Nx — проекции приложенных к телу сил на ось Ox; F ₁ _y, F ₂ _y, ..., F _Ny — проекции приложенных к телу сил на ось Oy.

Рис. 2.19

При поступательном движении материальной точки (тела) с ускорением $(\vec{a} \neq 0)$ равнодействующая сил равна произведению массы тела m на ускорение $\vec{a}$ (рис. 2.20):

$\vec{F} = m \vec{a}$ ,

т.е. при наличии ускорения вдоль одной из координатных осей (например, Ox) проекции равнодействующей на координатные оси определяются равенствами

F ₁ _x + F ₂ _x + ... + F _Nx = ma _x;

F ₁ _y + F ₂ _y + ... + F _Ny = 0,

где F ₁ _x, F ₂ _x, ..., F _Nx — проекции сил, приложенных к телу, на ось Ox; F ₁ _y, F ₂ _y, ..., F _Ny — проекции сил, приложенных к телу, на ось Oy.

Рис. 2.20

Выбор координатной оси целесообразно производить по направлению ускорения $(\vec{O x} ↑ ↑ \vec{a})$ ; тогда знак проекции ускорения (и проекции равнодействующей всех сил на указанную ось) будет положительным.

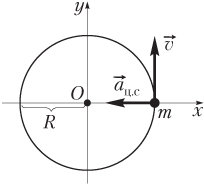
При движении материальной точки (тела) по окружности с постоянной по величине скоростью (рис. 2.21):

${\vec{F}}_{1} + {\vec{F}}_{2} + ... + {\vec{F}}_{N} = m {\vec{a}}_{ц . с}$ ,

где ${\vec{F}}_{1}$ , ${\vec{F}}_{2}$ , ..., ${\vec{F}}_{N}$ — силы, приложенные к телу; m — масса тела; ${\vec{a}}_{ц . с}$ — его центростремительное ускорение, направленное по радиусу к центру окружности, модуль которого может быть вычислен по одной из формул:

$a_{ц . с} = \frac{v^{2}}{R}$ , a _ц.с = ω²R, a _ц.с = vω,

где v — модуль скорости тела; R — радиус окружности; ω — величина угловой скорости тела.

Рис. 2.21

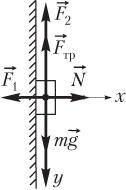
Пример 25. К вертикальной стене горизонтальной силой 12 Н прижимается брусок массой 0,50 кг. Найти модуль вертикально направленной силы, под действием которой брусок будет скользить вниз с постоянной скоростью. Коэффициент трения принять равным 0,10.

Решение. Силы, действующие на тело, показаны на рисунке.

При движении тела без ускорения второй закон Ньютона записывается в виде:

${\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{тр} + \vec{N} + m \vec{g} = 0$ ,

или в проекциях на координатные оси

$\begin{array}{l} O x : - F_{1} + N = 0, \\ O y : m g - F_{2} - F_{тр} = 0, \end{array}}$

где F _тр = µN — модуль силы трения; µ — коэффициент трения; N — модуль силы нормальной реакции опоры; F ₁ — модуль прижимающей силы; m — масса тела; g — модуль ускорения свободного падения; F ₂ — модуль искомой силы.

Из первого уравнения системы следует, что

N = F ₁;

следовательно, модуль силы трения определяется выражением

F _тр = µF ₁.

Подставляя F _тр во второе уравнение, получим формулу для расчета силы F ₂:

F ₂ = mg − F _тр = mg − µF ₁.

Произведем вычисление:

$F_{2} = 0,50 \cdot 10 - 0,10 \cdot 12 = 3,8$ Н.

Пример 26. Под действием двух взаимно перпендикулярных сил, модули которых равны 30 H и 40 Н, тело из состояния покоя за 4,0 с переместилось на 20 м вдоль направления равнодействующей силы. Найти массу тела.

Решение. Силы, действующие на тело, изображены на рисунке.

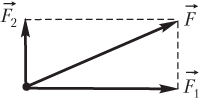
Перемещение тела происходит под действием двух сил по направлению их равнодействующей

$\vec{F} = {\vec{F}}_{1} + {\vec{F}}_{2}$ ,

величина которой в данном случае (силы взаимно перпендикулярны) вычисляется по формуле

$F = \sqrt{F_{1}^{2} + F_{2}^{2}}$ .

Значение ускорения определяется выражением

$S = \frac{a t^{2}}{2}$ ,

т.е.

$a = \frac{2 S}{t^{2}}$ ,

где S — пройденный телом путь; t — время движения тела.

С другой стороны, величина ускорения может быть определена по второму закону Ньютона:

$a = \frac{F}{m}$ ,

где m — масса тела; F — модуль равнодействующей.

Равенство

$\frac{2 S}{t^{2}} = \frac{F}{m}$ ,

записанное в явном виде

$\frac{2 S}{t^{2}} = \frac{\sqrt{F_{1}^{2} + F_{2}^{2}}}{m}$ ,

позволяет найти массу тела:

$m = \frac{t^{2} \sqrt{F_{1}^{2} + F_{2}^{2}}}{2 S} = \frac{{(4,0)}^{2} \sqrt{30^{2} + 40^{2}}}{2 \cdot 20} = 20$ кг.

Пример 27. Брусок массой 2,5 кг лежит на горизонтальной поверхности с коэффициентом трения 0,2. К бруску приложена сила, модуль которой возрастает линейно от 0 до 16 Н за 4,0 с. Определить ускорение тела через 5,0 с после начала действия силы. Сила направлена под углом 45° к горизонту.

Решение. Силы, действующие на тело, показаны на рисунке.

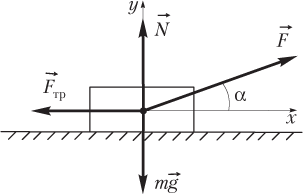
Определим, начнет ли тело двигаться в указанном интервале времени. Для этого найдем значение t ₀, при котором сила трения покоя достигнет максимального значения:

$F_{тр . пок}^{max} = μ N$ ,

где µ — коэффициент трения; $N = m g - F_{0} \sin α$ — модуль силы нормальной реакции опоры; m — масса тела; g — модуль ускорения свободного падения; F ₀ — значение силы, приложенной к телу под углом α, в момент начала движения.

С другой стороны, сила трения покоя определяется выражением

$F_{тр . пок} = F_{x}$ .

В момент достижения максимального значения она равна

$F_{тр . пок}^{max} = F_{0} \cos α$ .

Установим закон изменения величины силы F(t) с течением времени. Сила зависит от времени линейно; линейная зависимость силы от времени показана на рисунке и описывается уравнением

F(t) = kt,

где k = tg β; t — время, т.е. F(t) = 4t.

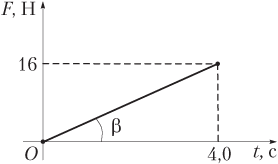
Подставим F ₀ = 4t ₀ в выражения для N и $F_{тр .пок}^{max}$ :

$N = m g - 4 t_{0} \sin α$ ,

$F_{тр . пок}^{max} = 4 t_{0} \cos α$ .

Из равенства

$μ (m g - 4 t_{0} \sin α) = 4 t_{0} \cos α$

следует, что искомый момент времени определяется формулой

$t_{0} = \frac{μ m g}{4 (μ \sin α + \cos α)}$ .

Вычисление дает значение

$t_{0} = \frac{0,2 \cdot 2,5 \cdot 10}{4 (0,2 \cdot 0,5 \sqrt{2} + 0,5 \sqrt{2})} \approx 1,5$ c.

Следовательно, тело начнет двигаться через 1,5 с после начала действия силы.

Для нахождения ускорения тела запишем основной закон динамики в виде

${\vec{F}}_{тр} + \vec{N} + \vec{F} + m \vec{g} = m \vec{a}$ ,

или в проекциях на координатные оси:

$\begin{array}{l} O x : - F_{тр} + 4 t \cos α = m a, \\ O y : - m g + N + 4 t \sin α = 0. \end{array}}$

Из второго уравнения системы выразим силу реакции опоры

$N = m g - 4 t \sin α$

и получим формулу для вычисления силы трения:

$F_{тр} = μ N = μ (m g - 4 t \sin α)$ .

Подставим это выражение в первое уравнение системы:

$a = \frac{4 t \cos α - μ (m g - 4 t \sin α)}{m} = 4 t \frac{\cos α + μ \sin α}{m} - μ g$

и найдем значение ускорения в момент времени t = 5 c:

$a = 4 \cdot 5,0 \cdot \frac{0,5 \sqrt{2} + 0,2 \cdot 0,5 \sqrt{2}}{2,5} - 0,2 \cdot 10 \approx 4,8$ м/с².

Пример 28. На легкой нерастяжимой нити длиной 1,5 м подвешен шарик массой 50 г. Пуля массой 10 г попадает в шарик и застревает в нем. В результате шарик приобретает скорость 12 м/с. Найти силу натяжения нити сразу после соударения шарика и пули.

Решение. Движение шарика с застрявшей в нем пулей происходит по окружности радиусом l под действием сил, показанных на рисунке.

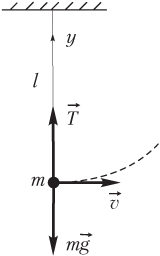
Следовательно, равнодействующая силы тяжести $m \vec{g}$ и силы натяжения нити $\vec{T}$ является центростремительной силой:

${\vec{F}}_{ц . с} = m \vec{g} + \vec{T}$ ,

где m = 50 + 10 = 60 г — масса шарика с застрявшей в нем пулей.

В проекции на ось Oy уравнение имеет вид:

$F_{ц . с} = T - m g$ ,

где T — модуль силы натяжения нити; m — суммарная масса шарика и пули; g — модуль ускорения свободного падения.

Однако движение шарика происходит с непостоянной скоростью. Второй закон Ньютона можно записать только для мгновенных значений T и v:

$T - m g = \frac{m v^{2}}{R}$ ,

где v — модуль мгновенной скорости; R = l — радиус окружности, равный длине нити.

Отсюда выразим искомое значение силы натяжения нити и рассчитаем ее значение:

$T = m (g + \frac{v^{2}}{R}) = (50 + 10) \cdot 10^{- 3} (10 + \frac{12^{2}}{1,5}) \approx 6,4$ Н.

Физика