Физика

Пример 34. На горизонтальном диске лежит маленький шарик. Определить угловую скорость вращения диска относительно вертикальной оси, при которой начнется скольжение шарика. Шарик расположен на расстоянии 10 см от указанной оси, а коэффициент трения между шариком и диском равен 0,5.

Решение. Данную задачу можно решать как в инерциальной системе отсчета (ИСО), так и в неинерциальной (НИСО).

1. Инерциальную систему отсчета свяжем с Землей.

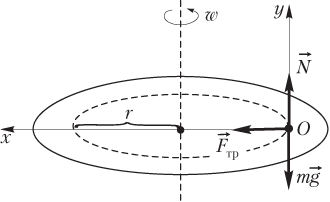
Силы, действующие на шарик в указанной системе отсчета, показаны на рисунке. Шарик относительно ИСО равномерно движется по окружности и обладает центростремительным ускорением.

Второй закон Ньютона в ИСО имеет вид:

${\overrightarrow{F}}_{\text{тр}}+m\overrightarrow{g}+\overrightarrow{N}=m{\overrightarrow{a}}_{\text{ц}.\text{с}}$,

или в проекциях на координатные оси:

$\begin{array}{l}Ox\text{: }{F}_{\text{тр}}=m{a}_{\text{ц}.\text{с}},\\ Oy\text{: }N-mg=\mathrm{0,}\end{array}\}$

где m — масса шарика; g — модуль ускорения свободного падения; F _тр = µN — модуль силы трения; N — модуль силы нормальной реакции опоры; µ — коэффициент трения; $a_{\text{ц}.\text{с}}={\omega }^{2}r$ — модуль центростремительного ускорения шарика; ω — модуль угловой скорости диска; r — радиус окружности, по которой происходит движение шарика (расстояние от центра диска до шарика).

С учетом явного вида выражений для a _ц.с и F _тр решение системы относительно угловой скорости дает:

$\omega =\sqrt{\frac{\mu g}{r}}=\sqrt{\frac{\mathrm{0,5}\cdot 10}{\mathrm{0,10}}}\approx \mathrm{7,1}$ рад/с.

2. Неинерциальную систему отсчета свяжем с той точкой диска, в которой находится шарик. Данная точка обладает центростремительным ускорением ${\overrightarrow{a}}^{*}$; именно поэтому система отсчета, связанная с указанной точкой, является неинерциальной.

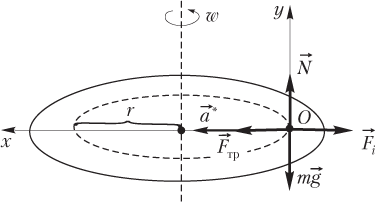
В НИСО, помимо сил взаимодействия шарика с другими телами, действует еще одна сила — сила инерции ${\overrightarrow{F}}_i$; направление данной силы противоположно направлению ускорения НИСО, т.е. ${\overrightarrow{a}}^{*}$.

Силы, действующие на шарик в указанной системе отсчета, показаны на рисунке. Шарик относительно НИСО покоится.

Второй закон Ньютона в НИСО имеет вид:

${\overrightarrow{F}}_{\text{тр}}+m\overrightarrow{g}+\overrightarrow{N}+{\overrightarrow{F}}_i=0$,

или в проекциях на координатные оси:

$\begin{array}{l}Ox\text{: }{F}_{\text{тр}}-F_i=\mathrm{0,}\\ Oy\text{: }N-mg=\mathrm{0,}\end{array}\}$

где $F_i=m{a}^{*}=m{\omega }^{2}r$ — модуль силы инерции.

С учетом явного вида выражений для силы трения и силы инерции решение системы относительно ω дает тот же результат, что и решение данной задачи в ИСО:

$\omega =\sqrt{\frac{\mu g}{r}}=\sqrt{\frac{\mathrm{0,5}\cdot 10}{\mathrm{0,10}}}\approx \mathrm{7,1}$ рад/с.

Таким образом, результат не зависит от выбора системы отсчета.

Пример 35. Бусинка скользит по обручу радиусом 50 см, который вращается относительно вертикальной оси, проходящей через его центр. На какую максимальную высоту может подняться бусинка относительно первоначального положения? Угловая скорость обруча равна 5,0 рад/c. Трением пренебречь.

Решение. Данную задачу можно решать как в инерциальной системе отсчета (ИСО), так и в неинерциальной (НИСО).

1. Инерциальную систему отсчета свяжем с Землей.

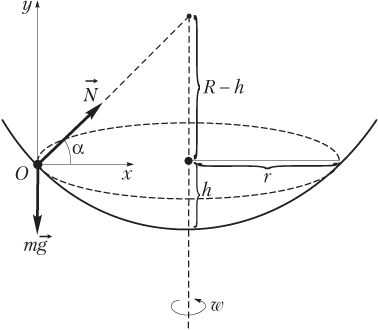
Силы, действующие на бусинку в указанной системе отсчета, показаны на рисунке. Бусинка относительно ИСО равномерно движется по окружности в горизонтальной плоскости и обладает центростремительным ускорением.

Второй закон Ньютона в ИСО имеет вид:

$\overrightarrow{N}+m\overrightarrow{g}=m{\overrightarrow{a}}_{\text{ц}.\text{с}}$,

или в проекциях на координатные оси:

$\begin{array}{l}Ox\text{: }N\cos \alpha =m{a}_{\text{ц}.\text{с}},\\ Oy\text{: }N\sin \alpha -mg=\mathrm{0,}\end{array}\}$

где m — масса бусинки; g — модуль ускорения свободного падения; N — модуль силы нормальной реакции обруча; $a_{\text{ц}.\text{с}}={\omega }^{2}r$ — модуль центростремительного ускорения бусинки; ω — модуль угловой скорости обруча; r — радиус окружности, по которой происходит движение бусинки; α — угол между силой $\overrightarrow{N}$ и осью Ox.

С учетом явного вида a _ц.с система уравнений может быть записана в виде:

$\begin{array}{l}Ox\text{: }N\cos \alpha =m{\omega }^{2}r,\\ Oy\text{: }N\sin \alpha =mg.\end{array}\}$

Деление уравнений дает:

$\frac{N\sin \alpha }{N\cos \alpha }=\frac{mg}{m{\omega }^{2}r}$,

или, после упрощения,

$\mathrm{tg}\alpha =\frac{g}{{\omega }^{2}r}$.

Однако радиус окружности, по которой происходит движение бусинки, неизвестен. Из геометрических соображений tg α определяется формулой

$\mathrm{tg}\alpha =\frac{R-h}{r}$,

где R — радиус обруча; h — высота, на которую поднялась бусинка относительно своего начального положения.

Равенство левых частей уравнений для tg α позволяет записать равенство их правых частей:

$\frac{g}{{\omega }^{2}r}=\frac{R-h}{r}$,

или

$\frac{g}{{\omega }^2}=R-h$.

Отсюда — искомая высота подъема бусинки

$h=R-\frac{g}{{\omega }^2}=\mathrm{0,5}-\frac{10}{{\mathrm{5,0}}^2}=\mathrm{0,1}\text{ м}=10\text{ см}$.

2. Неинерциальную систему отсчета свяжем с той точкой обруча, в которой находится бусинка. Данная точка обладает центростремительным ускорением ${\overrightarrow{a}}^{*}$; именно поэтому система отсчета, связанная с указанной точкой, является неинерциальной.

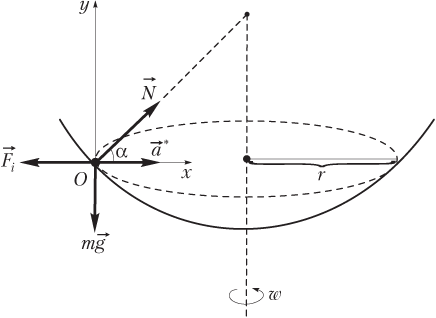
В НИСО, помимо сил взаимодействия бусинки с другими телами, действует еще одна сила — сила инерции ${\overrightarrow{F}}_i$; направление данной силы противоположно направлению ускорения указанной системы отсчета, т.е. ${\overrightarrow{a}}^{*}$.

Силы, действующие на бусинку в указанной системе отсчета, показаны на рисунке. Бусинка относительно НИСО покоится.

Второй закон Ньютона в НИСО имеет вид:

$m\overrightarrow{g}+\overrightarrow{N}+{\overrightarrow{F}}_i=0$,

или в проекциях на координатные оси:

$\begin{array}{l}Ox\text{: }N\cos \alpha -F_i=\mathrm{0,}\\ Oy\text{: }N\sin \alpha -mg=\mathrm{0,}\end{array}\}$

где $F_i=m{a}^{*}=m{\omega }^{2}r$ — модуль силы инерции.

С учетом явного вида F _i система уравнений может быть записана в виде:

$\begin{array}{l}Ox\text{: }N\cos \alpha =m{\omega }^{2}r,\\ Oy\text{: }N\sin \alpha =mg.\end{array}\}$

Полученная система уравнений полностью совпадает с системой уравнений, записанной при решении задачи в инерциальной системе отсчета. Следовательно, решение системы даст то же значение высоты подъема бусинки относительно ее начального положения.

Таким образом, выбор системы отсчета не влияет на полученный результат.