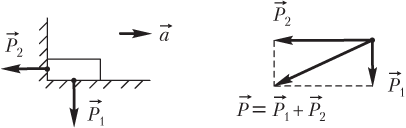Физика
Вес тела — это сила, с которой тело давит на опору или растягивает подвес. Вес всегда приложен к опоре или подвесу (но не к самому телу). Вес тела вычисляется по-разному в различных ситуациях.
Если опора или подвес неподвижны (или движутся равномерно и прямолинейно), то вес тела численно равен силе тяжести:
P = mg,
где m — масса тела; g — модуль ускорения свободного падения.
Если опора движется с ускорением , направленным вверх, то наблюдается увеличение веса на величину ma:
P = m(g + a),
где m — масса тела; g — модуль ускорения свободного падения; a — модуль ускорения опоры.
Если опора движется с ускорением , направленным вниз, то наблюдается уменьшение веса на величину ma:
P = m(g − a),
где m — масса тела; g — модуль ускорения свободного падения; a — модуль ускорения опоры.
Если ускорение опоры (или подвеса) направлено вниз и равно ускорению свободного падения (как по величине, так и по направлению), то вес тела обращается в ноль:
P = 0
и наступает состояние невесомости — тело перестает давить на опору (или растягивать подвес).
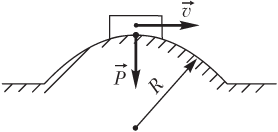
При движении тела по выпуклой поверхности с постоянной скоростью сила давления тела на опору (вес тела) в верхней точке траектории определяется формулой (рис. 2.3):
,
где m — масса тела; g — модуль ускорения свободного падения; v — модуль скорости тела; R — радиус кривизны траектории.
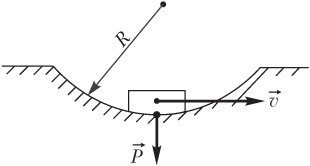
При движении тела по вогнутой поверхности с постоянной скоростью сила давления тела на опору (вес тела) в нижней точке траектории определяется формулой (рис. 2.4):
,
где m — масса тела; g — модуль ускорения свободного падения; v — модуль скорости тела; R — радиус кривизны траектории.
При движении комбинированной опоры, имеющей вертикальную и горизонтальную части (например, кресло водителя), с горизонтальным ускорением вес тела складывается из сил давлений на ее горизонтальную и вертикальную части, т.е. из P1 = mg и P2 = ma (рис. 2.5):
,
а модуль веса рассчитывается по формуле
,
где m — масса тела; g — модуль ускорения свободного падения; a — модуль (горизонтального) ускорения опоры.
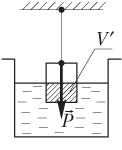
Если тело погружено в жидкость (или газ), то вес тела рассчитывается с учетом силы Архимеда, действующей на тело со стороны жидкости (или газа) (рис. 2.6):
,
где V′ — объем погруженной в жидкость (или газ) части тела; m — масса тела; g — модуль ускорения свободного падения; ρ0 — плотность жидкости (или газа).
Пример 8. Тело массой 1,5 кг лежит на дне сосуда с водой, причем 1/4 его объема остается над водой. Вычислить силу давления тела на дно сосуда, если плотность тела в 1,25 раза больше плотности воды. Считать, что вода подтекает под тело.
Решение. Для вычисления силы давления на дно сосуда воспользуемся формулой, позволяющей рассчитать вес тела, частично погруженного в жидкость:
,
где — объем погруженной части тела; — объем тела; ρ0 — плотность жидкости; m — масса тела; ρт — плотность тела; g — модуль ускорения свободного падения.
Запишем в явном виде формулу для расчета веса:
и произведем вычисления:
Н.
Пример 9. Найти силу давления пассажира на кресло гоночного автомобиля, движущегося по горизонтальному шоссе с ускорением 8,0 м/с2. Массу пассажира принять равной 75 кг.
Решение. Воспользуемся формулой для вычисления веса тела, оказывающего давление как на горизонтальную (mg), так и на вертикальную (ma) части опоры:
,
где m — масса пассажира; a — величина ускорения автомобиля; g — модуль ускорения свободного падения.
Произведем вычисления:
кН.
Пример 10. Во сколько раз вес пассажира гоночного автомобиля, движущегося с постоянной скоростью 25 м/с по выпуклому мосту радиусом 75 м, меньше его веса на участке траектории, имеющем вогнутую форму? Сравнить вес для самой высокой и самой низкой точек траектории.
Решение. Запишем формулы для вычисления веса пассажира:
- в самой высокой точке выпуклой траектории
,
- в самой низкой точке вогнутой траектории
,
где m — масса пассажира; v — величина скорости автомобиля; g — модуль ускорения свободного падения; R — радиус кривизны траектории.
Вес пассажира при движении автомобиля по вогнутой траектории превышает вес пассажира при движении по выпуклой траектории. Найдем отношение:
.
Расчет дает значение:
.
Таким образом, вес пассажира гоночного автомобиля в самой низкой точке траектории больше его веса в самой высокой точке траектории в 11 раз.
Пример 11. Во сколько раз будут отличаться показания пружинных весов, находящихся в кабине лифта при его движении с ускорением, направленным вверх, и с ускорением, направленным вниз? Величина ускорения равна 2,5 м/с2.
Решение. Вес тела, подвешенного к пружинным весам, находящимся в лифте, определяется формулами:
- при ускорении лифта, направленном вверх,
P1 = m(g + a),
- при ускорении лифта, направленном вниз,
P2 = m(g − a),
где m — масса тела; a — величина ускорения лифта; g — модуль ускорения свободного падения.
Вес тела при движении лифта с ускорением, направленным вверх, превышает вес тела при движении лифта с ускорением, направленным вниз. Найдем отношение веса тела в первом случае к весу тела во втором случае
.
Расчет дает значение:
.
Таким образом, вес тела при движении лифта с ускорением, направленным вверх, больше его веса при движении лифта с ускорением, направленным вниз, приблизительно в 1,7 раза.
Пример 12. Некоторое тело, подвешенное к пружинным весам, полностью погружено в жидкость, плотность которой в 2,5 раза меньше плотности тела, и находится в лифте. Показания пружинных весов различаются в зависимости от направления ускорения лифта. Найти отношение максимального показания весов к их минимальному показанию при значении ускорения 2,5 м/с2.
Решение. Вес тела, погруженного в жидкость и подвешенного к пружинным весам, находящимся в лифте, определяется формулами:
- при ускорении лифта, направленном вверх, —
P1 = m(g + a) − ρ0gV,
- при ускорении лифта, направленном вниз, —
P2 = m(g − a) − ρ0gV,
где m — масса тела; a — величина ускорения лифта; g — модуль ускорения свободного падения; V = m/ρт — объем тела; ρ0 — плотность жидкости; ρт — плотность тела.
Вес тела при движении лифта с ускорением, направленным вверх, превышает вес тела при движении лифта с ускорением, направленным вниз. Отношение веса тела в первом случае к весу тела во втором случае определяется формулой
.
Произведем преобразование записанной формулы, выполнив замену:
,
т.е.
.
Подстановка данных дает значение искомого отношения:
.
Таким образом, вес тела при движении лифта с ускорением, направленным вверх, больше его веса при движении лифта с ускорением, направленным вниз, в 2,4 раза.