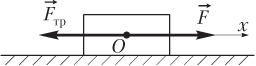Предметы

Физика

Динамика

2.2. Силы

2.2.4. Сила трения

Теория Тренинг

Физика

Общий тест

2.2. Силы

2.2.4. Сила трения

Сила трения действует не только на движущееся тело, но и на тело, находящееся в покое, если существуют силы, которые стремятся этот покой нарушить. На тело, которое катится по опоре, также действует сила трения.

Сила трения покоя численно равна составляющей силы, направленной вдоль поверхности, на которой находится данное тело, и стремящейся сдвинуть его с места (рис. 2.7):

F_тр.пок = F_x.

Рис. 2.7

При достижении указанной составляющей некоторого критического значения (F_x = F_крит) тело начинает двигаться. Критическое значение силы, которое соответствует началу движения, определяется формулой

F_x = F_крит = µ_покN,

где µ_пок — коэффициент трения покоя; N — модуль силы нормальной реакции опоры (эта сила численно равна весу тела).

В момент начала движения сила трения покоя достигает максимального значения:

$F_{тр . пок}^{max} = μ_{пок} N$ .

Сила трения скольжения постоянна и определяется произведением:

F_тр.ск = µ_скN,

где µ_ск — коэффициент трения скольжения; N — модуль силы нормальной реакции опоры.

При решении задач считают, что коэффициенты трения покоя µ_пок и скольжения µ_ск равны между собой:

µ_пок = µ_ск = µ.

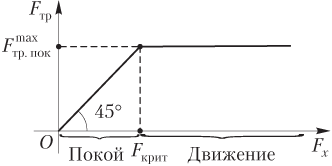
На рис. 2.8 изображен график зависимости величины силы трения F_тр от проекции силы F_x, стремящейся сдвинуть тело, на ось, направленную вдоль поверхности предполагаемого движения.

Рис. 2.8

Для того чтобы определить, будет ли данное тело находиться в покое или начнет двигаться под действием приложенной силы определенной величины и направления, необходимо:

1) рассчитать критическое значение силы, достаточной для того, чтобы вызвать движение тела, по формуле

F_крит = µN,

где µ — коэффициент трения; N — модуль силы нормальной реакции опоры;

2) рассчитать значение составляющей приложенной силы F_x вдоль оси предполагаемого движения исходя из условия задачи;

3) сравнить значения F_крит и F_x:

если F_x > F_крит, то тело движется под действием приложенной силы; в этом случае сила трения скольжения рассчитывается как

F_тр.ск = µN;

если F_x < F_крит, то тело покоится под действием приложенной силы; в этом случае сила трения покоя рассчитывается как

F_тр.пок = F_x.

Модуль силы трения качения F_тр.кач пропорционален коэффициенту трения качения µ_кач, модулю силы нормальной реакции опоры N и обратно пропорционален радиусу R катящегося тела:

$F_{тр . кач} = μ_{кач} \frac{N}{R}$ .

Пример 13. К телу массой 6,0 кг, лежащему на горизонтальной поверхности, приложена сила 25 Н, направленная вдоль поверхности. Найти силу трения, если коэффициент трения равен 0,5.

Решение. Произведем оценку величины силы, способной вызвать движение тела, по формуле

F_кр = µN,

где µ — коэффициент трения; N — модуль силы нормальной реакции опоры, численно равной весу тела (P = mg).

Величина критической силы, достаточной для начала движения тела, составляет

$F_{кр} = μ m g = 0,5 \cdot 6,0 \cdot 10 = 30$ Н.

Проекция силы, приложенной к телу в горизонтальном направлении, на ось предполагаемого движения Ox (см. рисунок) равна

F_x = F = 25 Н.

Таким образом, имеет место неравенство

F_x < F_кр,

т.е. величина приложенной к телу силы меньше величины силы, способной вызвать его движение. Следовательно, тело находится в состоянии покоя.

Искомая сила трения — сила трения покоя — равна внешней горизонтальной силе, стремящейся этот покой нарушить:

F_тр.пок = F_x = 25 Н.

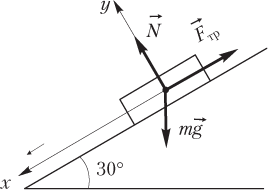
Пример 14. Тело находится на наклонной плоскости с углом при основании 30°. Вычислить силу трения, если коэффициент трения равен $0,5 \sqrt{3}$ . Масса тела равна 3,0 кг.

Решение. На рисунке стрелкой показано направление предполагаемого движения.

Выясним, останется ли тело в покое или начнет двигаться. Для этого рассчитаем величину критической силы, способной вызвать движение, т.е.

F_кр = µN,

где µ — коэффициент трения; N = mg cos α — величина силы нормальной реакции наклонной плоскости.

Расчет дает значение указанной силы:

$F_{кр} = μ m g \cos 30 ° = 0,5 \sqrt{3} \cdot 3,0 \cdot 10 \cdot \frac{\sqrt{3}}{2} = 22,5$ Н.

Из состояния покоя тело стремится вывести проекция силы тяжести на ось Ox, величина которой составляет

F_x = mg sin 30° = 15 Н.

Таким образом, имеет место неравенство

F_x < F_кр,

т.е. проекция силы, стремящейся вызвать движение тела, меньше величины силы, способной это сделать. Следовательно, тело сохраняет состояние покоя.

Искомая сила — сила трения покоя — равна

F_тр = F_x = 15 Н.

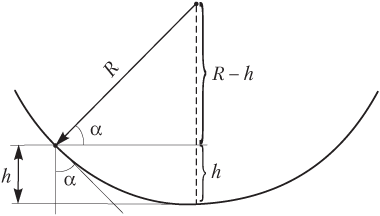
Пример 15. Шайба находится на внутренней поверхности полусферы на высоте 10 см от нижней точки. Радиус полусферы составляет 50 см. Вычислить коэффициент трения шайбы о сферу, если известно, что указанная высота является максимально возможной.

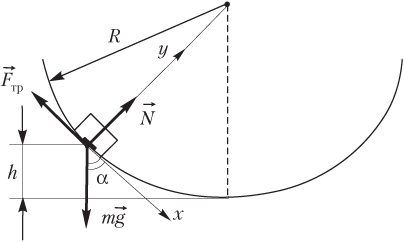
Решение. Проиллюстрируем условие задачи рисунком.

Шайба, согласно условию задачи, находится на максимально возможной высоте. Следовательно, сила трения покоя, действующая на шайбу, имеет максимальное значение, совпадающее с проекцией силы тяжести на ось Ox:

$F_{тр . пок}^{max} = F_{x}$ ,

где F_x = mg cos α — модуль проекции силы тяжести на ось Ox; m — масса шайбы; g — модуль ускорения свободного падения; α — угол, показанный на рисунке.

Максимальная сила трения покоя совпадает с силой трения скольжения:

$F_{тр . пок}^{max} = F_{тр . ск}$ ,

где F_тр.ск = µN — модуль силы трения скольжения; N = mg sin α — величина силы нормальной реакции поверхности полусферы; µ — коэффициент трения.

Коэффициент трения определим, записав указанное равенство в явном виде:

mg cos α = µmg sin α.

Отсюда следует, что искомый коэффициент трения определяется тангенсом угла α:

$μ = \frac{1}{tg α}$ .

Указанный угол определим из дополнительного построения:

$tg α = \frac{R - h}{\sqrt{2 h R - h^{2}}}$ ,

где h — предельная высота, на которой может находиться шайба; R — радиус полусферы.

Расчет дает значение тангенса:

$tg α = \frac{0,5 - 0,1}{\sqrt{2 \cdot 0,1 \cdot 0,5 - {(0,1)}^{2}}} = \frac{4}{3}$

и позволяет вычислить искомый коэффициент трения:

$μ = \frac{1}{tg α} = \frac{3}{4} = 0,75$ .