Предметы

Физика

Динамика

2.2. Силы

2.2.1. Сила гравитационного притяжения (сила тяжести)

Теория Тренинг

Физика

Общий тест

2.2. Силы

2.2.1. Сила гравитационного притяжения (сила тяжести)

Сила тяжести действует на любое тело, находящееся вблизи поверхности планеты. Без учета суточного вращения планеты (вращения планеты вокруг собственной оси) сила тяжести совпадает с силой притяжения тела к планете и определяется законом всемирного тяготения.

Закон всемирного тяготения: любые две материальные точки притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

$F = \frac{G m_{1} m_{2}}{r^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ м³/(кг ⋅ с²) — универсальная гравитационная постоянная; m₁ и m₂ — массы материальных точек; r — расстояние между материальными точками.

Универсальную гравитационную постоянную можно также измерять в (Н ⋅ м²/кг²), что непосредственно вытекает из закона всемирного тяготения. Для удобства далее будем использовать значение G = 6,67 ⋅ 10⁻¹¹ Н ⋅ м²/кг².

Закон всемирного тяготения применим не только для материальных точек, но и для тел, имеющих сферически симметричное распределение массы; однако в этом случае под r следует понимать расстояние между центрами тел.

На любое тело, находящееся на поверхности планеты, действует сила притяжения:

$F_{0} = \frac{G m M}{R^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ Н ⋅ м²/кг² — универсальная гравитационная постоянная; m — масса тела; M — масса планеты; R — ее радиус.

Сила притяжения (далее — сила тяжести) может быть рассчитана также по формуле

F₀ = mg₀,

где g₀ — ускорение свободного падения на поверхности планеты.

На любое тело, находящееся на высоте h над поверхностью планеты, действует сила притяжения:

$F = \frac{G m M}{{(R + h)}^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ Н ⋅ м²/кг² — универсальная гравитационная постоянная; m — масса тела; M — масса планеты; R — радиус.

Сила тяжести в этом случае может быть записана в виде:

F = mg,

где g — ускорение свободного падения на указанной высоте.

В зависимости от положения тела по отношению к поверхности планеты ускорение свободного падения определяется по-разному:

на поверхности планеты

$g_{0} = \frac{G M}{R^{2}}$ ;

на высоте h над поверхностью планеты

$g = \frac{G M}{{(R + h)}^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ Н ⋅ м²/кг² — универсальная гравитационная постоянная; M — масса планеты; R — радиус планеты;

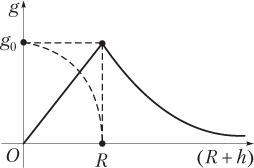
на глубине h под поверхностью планеты ускорение свободного падения убывает по линейному закону (рис. 2.1).

Рис. 2.1

На поверхности Земли ускорение свободного падения определяется формулой

$g_{З} = \frac{G M_{З}}{R_{З}^{2}}$

и составляет g_З ≈ 10 м/с², где G = 6,67 ⋅ 10⁻¹¹ Н ⋅ м²/кг² — универсальная гравитационная постоянная; M_З — масса Земли; R_З — радиус Земли.

Пример 1. Радиус некоторой планеты в 3 раза больше радиуса Земли, а плотность — в 2 раза меньше. Определить ускорение свободного падения на этой планете.

Решение. Дважды запишем формулу для ускорения свободного падения:

для поверхности Земли

$g_{0} = \frac{G M_{З}}{R_{З}^{2}}$ ;

для поверхности планеты

$g = \frac{G M}{R^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ Н · м²/кг² — универсальная гравитационная постоянная; M_З — масса Земли; R_З — радиус Земли; M — масса планеты; R — радиус планеты.

Отношение уравнений

$\frac{g_{0}}{g} = \frac{M_{З}}{M} \frac{R^{2}}{R_{З}^{2}}$

позволяет получить формулу для вычисления ускорения свободного падения для поверхности планеты:

$g = g_{0} \frac{M}{M_{З}} {(\frac{R_{З}}{R})}^{2}$ .

Считая, что планеты имеют шарообразную форму, определим их массы:

масса Земли

$M_{З} = \frac{4}{3} π R_{З}^{3} ρ_{З}$ ;

масса планеты

$M = \frac{4}{3} π R^{3} ρ$ ,

где ρ_З — плотность Земли; $V_{З} = \frac{4}{3} π R_{З}^{3}$ — объем Земли (шара радиусом R_З); ρ — плотность планеты; $V = \frac{4}{3} π R^{3}$ — объем планеты (шара радиусом R).

Отношение масс определяется выражением

$\frac{M}{M_{З}} = \frac{ρ}{ρ_{З}} {(\frac{R}{R_{З}})}^{3}$ .

Подставим (M/M_З) в формулу для вычисления g:

$g = g_{0} \frac{M}{M_{З}} {(\frac{R_{З}}{R})}^{2} = g_{0} \frac{ρ}{ρ_{З}} {(\frac{R}{R_{З}})}^{3} {(\frac{R_{З}}{R})}^{2} = g_{0} \frac{ρ}{ρ_{З}} \frac{R}{R_{З}}$ ,

где R = 3R_З — заданное в условии соотношение радиусов Земли и планеты; ρ_З = 2ρ — заданное в условии соотношение между их плотностями.

Преобразования дают окончательную формулу для расчета ускорения свободного падения на поверхности планеты:

$g = g_{0} \frac{ρ}{2 ρ} \frac{3 R_{З}}{R_{З}} = 1,5 g_{0}$ .

Считая, что ускорение свободного падения на поверхности Земли имеет значение g₀ ≈ 10 м/с², получим величину ускорения свободного падения на поверхности планеты:

$g = 1,5 g_{0} \approx 1,5 \cdot 10 = 15$ м/с².

Пример 2. Два одинаковых шара радиусами 1,5 м соприкасаются поверхностями. Считая шары однородными, найти, во сколько раз уменьшится модуль силы притяжения, если один из шаров сдвинуть на 1,0 м вдоль линии, соединяющей центры шаров.

Решение. Покажем расположение шаров на рисунке: первоначальное (a), конечное (б).

Для решения задачи применим закон всемирного тяготения, записав соответствующую формулу дважды:

для первоначального расположения шаров —

$F_{1} = \frac{G m^{2}}{r_{1}^{2}} = \frac{G m^{2}}{{(2 R)}^{2}}$ ,

для конечного расположения шаров —

$F_{2} = \frac{G m^{2}}{r_{2}^{2}} = \frac{G m^{2}}{{(2 R + l)}^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ Н · м²/кг² — универсальная гравитационная постоянная; m — масса каждого шара; R — радиус каждого шара; r₁ = 2R — первоначальное расстояние между центрами шаров; r₂ = (2R + l) — расстояние между центрами шаров после перемещения шаров на расстояние l.

Искомое отношение сил составляет

$\frac{F_{1}}{F_{2}} = \frac{G m^{2}}{{(2 R)}^{2}} \frac{{(2 R + l)}^{2}}{G m^{2}} = \frac{{(2 R + l)}^{2}}{{(2 R)}^{2}} = {(\frac{2 R + l}{2 R})}^{2}$ .

Произведем вычисление:

$\frac{F_{1}}{F_{2}} = {(\frac{2 \cdot 1,5 + 1,0}{2 \cdot 1,5})}^{2} = {(\frac{4,0}{3,0})}^{2} \approx 1,8$ .

Сила притяжения между шарами после увеличения расстояния между ними уменьшилась приблизительно в 1,8 раза.

Пример 3. Какая сила притягивает тело, находящееся на поверхности Луны? Известно, что это же тело, находясь на поверхности Земли, притягивается к ней с силой 0,20 кН. Ускорение свободного падения на поверхности Луны считать равным 1,7 м/с².

Решение. На поверхности Луны и на поверхности Земли на одно и то же тело действуют различные силы притяжения:

на поверхности Луны —

F_Л = mg;

на поверхности Земли —

F_З = mg₀,

где m — масса тела; g₀ = 10 м/с² — модуль ускорения свободного падения на поверхности Земли; g = 1,7 м/с² — модуль ускорения свободного падения на поверхности Луны.

Отношение сил (F_Л/F_З) равно отношению соответствующих модулей ускорения свободного падения (g/g₀), т.е.

$\frac{F_{Л}}{F_{З}} = \frac{g}{g_{0}}$ ,

и позволяет вычислить искомую силу:

$F_{Л} = F_{З} \frac{g}{g_{0}} = 0,2 \cdot 10^{3} \cdot \frac{1,7}{10} = 34$ Н.

Пример 4. Вычислить ускорение свободного падения на высоте, равной утроенному радиусу планеты, если известно, что на ее поверхности тело массой 3,0 кг притягивается силой 45 Н.

Решение. Ускорение свободного падения на некоторой высоте над поверхностью планеты определяется формулой

$g = \frac{G M}{{(R + h)}^{2}}$ ,

где G = 6,67 ⋅ 10⁻¹¹ Н · м²/кг² — универсальная гравитационная постоянная; M — масса планеты; R — радиус планеты; h = 3R — высота над поверхностью планеты.

Подстановка h = 3R в записанную формулу дает:

$g = \frac{G M}{{(R + 3 R)}^{2}} = \frac{G M}{16 R^{2}}$ .

Однако в задаче не заданы ни масса, ни радиус планеты.

Величину (GM/R²) найдем, записав формулу для расчета силы притяжения, действующей на тело, находящееся на поверхности данной планеты:

$F_{0} = \frac{G M m}{R^{2}}$ ,

где m — масса тела; F₀ — величина силы, действующей на тело, находящееся на поверхности планеты.

Отсюда следует, что

$\frac{G M}{R^{2}} = \frac{F_{0}}{m}$ .

Подставляя полученное отношение в формулу для вычисления g, получим:

$g = \frac{G M}{16 R^{2}} = \frac{F_{0}}{16 m} = \frac{45}{16 \cdot 3,0} \approx 0,94$ м/с².