Предметы

Физика

Законы сохранения

3.5. Законы сохранения и изменения энергии

3.5.2. Закон сохранения полной механической энергии. Сохранение энергии при абсолютно упругом столкновении

Теория Тренинг

Физика

Общий тест

3.5. Законы сохранения и изменения энергии

3.5.2. Закон сохранения полной механической энергии. Сохранение энергии при абсолютно упругом столкновении

При соблюдении определенных условий полная механическая энергия системы тел не изменяется.

Если на систему не действуют внешние силы (система замкнута), а между телами системы не действуют силы трения (сопротивления), то полная механическая энергия системы сохраняется. Это утверждение носит название закона сохранения полной механической энергии и записывается в виде:

∆E = 0, или E₂ = E₁,

где E₁ — полная механическая энергия системы в начальном состоянии; E₂ — полная механическая энергия системы в конечном состоянии.

При решении задач закон сохранения полной механической энергии удобно записывать в явном виде:

W_k₁ + W_p₁ = W_k₂ + W_p₂,

где W_k₁ + W_p₁ = E₁ — полная механическая энергия системы в начальном состоянии; W_k₁ — начальная кинетическая энергия системы; W_p₁ — ее начальная потенциальная энергия; W_k₂ + W_p₂ = E₂ — полная механическая энергия системы в конечном состоянии; W_k₂ — конечная кинетическая энергия системы; W_p₂ — ее конечная потенциальная энергия.

Из закона сохранения полной механической энергии, записанного в явном виде, следует:

∆W_k = −∆W_p,

т.е. изменение кинетической энергии системы ∆W_k равно убыли (знак «минус») ее потенциальной энергии ∆W_p.

Таким образом, механическая энергия может превращаться из одного ее вида в другой (потенциальная в кинетическую и наоборот).

Важным приложением закона сохранения полной механической энергии является абсолютно упругое столкновение (удар) двух и более тел.

Абсолютно упругий удар — это столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после него снова превращается в кинетическую энергию.

При абсолютно упругом ударе выполняются:

закон сохранения полной механической (кинетической) энергии:

$\frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} = \frac{m_{1} u_{1}^{2}}{2} + \frac{m_{2} u_{2}^{2}}{2}$ ;

закон сохранения импульса:

$m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} = m_{1} {\vec{u}}_{1} + m_{2} {\vec{u}}_{2}$ ,

где m₁ и m₂ — массы соударяющихся тел; ${\vec{v}}_{1}$ и ${\vec{v}}_{2}$ — скорости первого и второго тела до столкновения; ${\vec{u}}_{1}$ и ${\vec{u}}_{2}$ — скорости тел после столкновения.

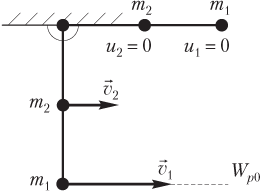
Пример 33. Вертикальный невесомый стержень длиной 12 м подвешен одним концом к оси вращения. На другом конце и в середине стержня закреплены две равные точечные массы. Какую минимальную скорость нужно сообщить нижнему концу стержня, чтобы он отклонился в горизонтальное положение?

Решение. На рисунке показаны два положения стержня с закрепленными на нем точечными массами: вертикальное (первое) и горизонтальное (второе); также показан нулевой уровень потенциальной энергии.

Обозначим величину минимальной скорости, которую необходимо сообщить точечной массе m₁, закрепленной на нижнем конце стержня, для отклонения стержня в горизонтальное положение — v₁. Тогда точечная масса m₂, закрепленная в середине стержня, имеет скорость, величина которой равна v₂. Стержень является твердым телом, поэтому угловая скорость всех его точек одинакова:

$ω = \frac{v_{1}}{l} = \frac{v_{2}}{0,5 l}$ ,

где l — расстояние от точечной массы m₁ до оси вращения; 0,5l — расстояние от точечной массы m₂ до оси вращения.

Отсюда следует соотношение между модулями скоростей конца и середины стержня:

v₂ = 0,5v₁.

Полная механическая энергия стержня с закрепленными на нем массами складывается из потенциальной и кинетической энергий указанных масс:

в первом состоянии системы

$E_{1} = m_{1} g h_{1} + m_{2} g h_{2} + \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2}$ ;

во втором состоянии системы

$E_{2} = m_{1} g H_{1} + m_{2} g H_{2} + \frac{m_{1} u_{1}^{2}}{2} + \frac{m_{2} u_{2}^{2}}{2}$ ,

где h₁ = 0 — высота, на которой расположена масса m₁ над нулевым уровнем потенциальной энергии в первом состоянии стержня; h₂ = 0,5l — высота, на которой расположена масса m₂ над нулевым уровнем в первом состоянии стержня; v₁ и v₂ — модули скоростей масс m₁ и m₂ в первом состоянии стержня соответственно; H₁ = H₂ = l — высоты, на которых расположены массы m₁ и m₂ во втором состоянии стержня соответственно; u₁ = u₂ = 0 — скорости масс m₁ и m₂ во втором состоянии стержня соответственно; g — модуль ускорения свободного падения.

С учетом значений высот и скоростей полная механическая энергия системы в явном виде определяется формулами:

в первом состоянии системы

$E_{1} = 0,5 m_{2} g l + 0,5 m_{1} v_{1}^{2} + 0,125 m_{2} v_{1}^{2}$ ;

во втором состоянии системы

E₂ = m₁gl + m₂gl.

В процессе движения внешние силы на систему не действуют; скорость, сообщенная концу стержня, будет иметь минимальное значение в отсутствие трения в системе. Поэтому полная механическая энергия системы сохраняется:

E₁ = E₂,

или в явном виде с учетом равенства масс (m₁ = m₂ = m)

$0,5 g l + 0,625 v_{1}^{2} = 2 g l$ .

Выразим отсюда модуль искомой скорости:

$v_{1} = \sqrt{2,4 g l}$

и рассчитаем ее значение:

$v_{1} = \sqrt{2,4 \cdot 10 \cdot 12} \approx 17$ м/с.

Пример 34. При выстреле вертикально вверх пуля массой 10,0 г вылетает из ствола ружья со скоростью 500 м/с. Определить изменение потенциальной энергии пули к моменту достижения максимальной высоты. Сопротивление воздуха отсутствует.

Решение. Нулевой уровень потенциальной энергии пули выберем на поверхности Земли.

Полная механическая энергия пули относительно поверхности Земли определяется суммой потенциальной и кинетической энергии:

при вылете пули из ствола ружья

E₁ = W_p₁ + W_k₁;

к моменту поднятия пули на максимальную высоту

E₂ = W_p₂ + W_k₂,

где W_p₁ — потенциальная энергия пули при вылете из ствола ружья; W_k₁ — кинетическая энергия пули при вылете из ствола ружья; W_p₂ — потенциальная энергия пули в момент поднятия на максимальную высоту; W_k₂ = 0 — кинетическая энергия пули в момент поднятия на максимальную высоту.

Внешние силы на пулю не действуют, сопротивление воздуха отсутствует. Поэтому выполняется закон сохранения полной механической энергии:

E₁ = E₂,

или в явном виде

W_p₁ + W_k₁ = W_p₂ + W_k₂.

Отсюда следует, что искомое изменение потенциальной энергии определяется равенством:

∆W_p = W_p₂ − W_p₁ = W_k₁ − W_k₂ = W_k₁,

где $W_{k 1} = \frac{m v_{0}^{2}}{2}$ — кинетическая энергия пули при вылете из ствола ружья; m — масса пули; v₀ — модуль начальной скорости пули.

Таким образом, изменение потенциальной энергии пули

$Δ W_{p} = \frac{m v_{0}^{2}}{2}$ .

Произведем вычисление:

$Δ W_{p} = \frac{10,0 \cdot 10^{- 3} \cdot 500^{2}}{2} = 1,25 \cdot 10^{3} Дж = 1,25$ кДж.

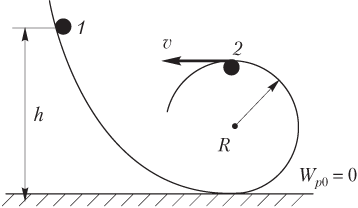
Пример 35. Небольшое тело массой 1,0 кг начинает соскальзывать с высоты 5,0 м по гладкому наклонному желобу, переходящему в «мертвую петлю» радиусом 1,0 м. Определить кинетическую энергию тела в момент прохождения им верхней точки «мертвой петли». Сопротивлением воздуха и силами трения в системе пренебречь.

Решение. На рисунке показаны два положения тела: в начале скольжения по желобу (первое) и в верхней точке «мертвой петли» (второе); также показан нулевой уровень потенциальной энергии.

Полная механическая энергия тела определяется суммой потенциальной и кинетической энергии:

в первом положении

E₁ = W_p₁ + W_k₁;

во втором положении

E₂ = W_p₂ + W_k₂,

где W_p₁ — потенциальная энергия тела в момент начала скольжения по желобу; W_k₁ = 0 — кинетическая энергия тела в момент начала скольжения по желобу; W_p₂ — потенциальная энергия тела в верхней точке «мертвой петли»; W_k₂ — кинетическая энергия тела в верхней точке «мертвой петли».

Внешние силы на тело не действуют, сопротивление воздуха и силы трения в системе отсутствуют. Поэтому выполняется закон сохранения полной механической энергии:

E₁ = E₂,

или в явном виде

W_p₁ + W_k₁ = W_p₂ + W_k₂.

Отсюда следует, что искомое значение кинетической энергии тела в верхней точке «мертвой петли» определяется равенством:

W_k₂ = W_p₁ + W_k₁ − W_p₂ = W_p₁ − W_p₂,

где W_p₁ = mgh — потенциальная энергия тела в момент начала скольжения по желобу; W_p₂ = 2mgR — потенциальная энергия тела в верхней точке «мертвой петли»; m — масса тела; g — модуль ускорения свободного падения; h — высота тела над нулевым уровнем потенциальной энергии в момент начала скольжения по желобу; R — радиус «мертвой петли».

Таким образом, искомая кинетическая энергия тела

W_k₂ = mg(h − 2R).

Вычисление дает ее значение:

W_k₂ = 1,0 ⋅ 10 ⋅ (5,0 − 2 ⋅ 1,0) = 30 Дж.