Предметы

Физика

Законы сохранения

3.6. Превращение механической энергии в теплоту. Выделение теплоты при абсолютно неупругом столкновении

3.6.1. Превращение механической энергии в теплоту. Выделение теплоты при абсолютно неупругом столкновении

Теория Тренинг

Физика

Общий тест

3.6. Превращение механической энергии в теплоту. Выделение теплоты при абсолютно неупругом столкновении

3.6.1. Превращение механической энергии в теплоту. Выделение теплоты при абсолютно неупругом столкновении

Вследствие изменения полной механической энергии системы может выделяться теплота.

Наличие сил трения (сопротивления) между телами замкнутой системы приводит к выделению энергии в виде теплоты:

Q = E₁ − E₂,

где E₁ — полная механическая энергия системы в начальном состоянии; E₂ — полная механическая энергия системы в конечном состоянии.

Если теплота в механической системе выделяется в результате совершения работы силами трения, то количество выделившейся при этом теплоты может быть рассчитано по формуле

$Q = | A_{тр} |$

где A_тр — работа, совершенная силами трения.

Превращение части механической энергии в теплоту происходит при абсолютно неупругом столкновении (ударе) двух и более тел.

Абсолютно неупругий удар — это столкновение тел, в результате которого тела объединяются и продолжают двигаться как единое целое.

Для абсолютно неупругого удара двух тел:

выполняется закон сохранения импульса:

$m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} = (m_{1} + m_{2}) \vec{u}$ ;

не выполняется закон сохранения полной механической (кинетической) энергии:

$\frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} \neq \frac{(m_{1} + m_{2}) u^{2}}{2}$ ,

где m₁ и m₂ — массы соударяющихся тел; ${\vec{v}}_{1}$ и ${\vec{v}}_{2}$ — скорости тел до столкновения; (m₁ + m₂) — масса тела, образовавшегося в результате удара; $\vec{u}$ — скорость тела, образовавшегося в результате удара.

Разность энергий до и после столкновения равна теплоте, выделившейся в процессе столкновения:

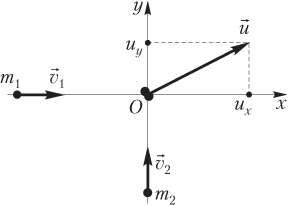
$Q = \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} - \frac{(m_{1} + m_{2}) u^{2}}{2}$ .

Пример 36. Какая доля энергии двух движущихся с равными по модулю скоростями тел, направленными под прямым углом друг к другу, перейдет в теплоту при абсолютно неупругом ударе? Массы тел относятся как 1:2.

Решение. На рисунке показаны два положения системы тел: до удара и сразу после удара. До удара тела движутся: первое — в положительном направлении оси Ox, второе — в положительном направлении оси Oy. Столкновение тел (абсолютно неупругий удар) происходит в начале системы координат. В результате абсолютно неупругого удара тела объединяются и движутся как единое целое со скоростью $\vec{u}$ .

Полная механическая энергия системы является кинетической энергией:

до удара

E₁ = W_k₁ + W_k₂;

после удара

E₂ = W_k,

где $W_{k 1} = \frac{m_{1} v_{1}^{2}}{2}$ — кинетическая энергия первого тела до удара; $W_{k 2} = \frac{m_{2} v_{2}^{2}}{2}$ — кинетическая энергия второго тела до удара; m₁ — масса первого тела; m₂ — масса второго тела; v₁ — модуль скорости первого тела до удара; v₂ — модуль скорости второго тела до удара; $W_{k} = \frac{(m_{1} + m_{2}) u^{2}}{2}$ — кинетическая энергия объединенного тела после удара; (m₁ + m₂) — масса объединенного тела после удара; u — модуль скорости объединенного тела после удара.

Теплота, выделившаяся в результате абсолютно неупругого удара, определяется разностью полных механических энергий системы до удара и после него:

Q = E₁ − E₂.

Для ее вычисления необходимо определить скорость объединенного тела.

Воспользуемся законом сохранения импульса, записав его в виде:

$m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} = (m_{1} + m_{2}) \vec{u}$ ,

или в проекциях на координатные оси,

$\begin{array}{l} O x : m_{1} v_{1} = (m_{1} + m_{2}) u_{x}; \\ O y : m_{2} v_{2} = (m_{1} + m_{2}) u_{y} . \end{array}}$

Выразим отсюда проекции скорости объединенного тела:

$\begin{array}{l} u_{x} = \frac{m_{1} v_{1}}{m_{1} + m_{2}} \\ u_{y} = \frac{m_{2} v_{2}}{m_{1} + m_{2}} \end{array}}$

и подставим их в формулу, определяющую квадрат скорости объединенного тела:

$u^{2} = u_{x}^{2} + u_{y}^{2} = {(\frac{m_{1} v_{1}}{m_{1} + m_{2}})}^{2} + {(\frac{m_{2} v_{2}}{m_{1} + m_{2}})}^{2}$ .

Полная механическая энергия объединенного тела, таким образом, определяется формулой

$E_{2} = \frac{(m_{1} + m_{2}) u^{2}}{2} = \frac{(m_{1} + m_{2})}{2} [{(\frac{m_{1} v_{1}}{m_{1} + m_{2}})}^{2} + {(\frac{m_{2} v_{2}}{m_{1} + m_{2}})}^{2}]$ .

С учетом

равенства модулей скоростей тел до удара:

v₁ = v₂ = v;

соотношения между массами тел:

m₁ = m,

m₂ = 2m,

m₁ + m₂ = 3m,

запишем полные механические энергии системы:

до удара

$E_{1} = \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} = \frac{m v^{2}}{2} + \frac{2 m v^{2}}{2} = \frac{3}{2} m v^{2}$ ;

после удара

$E_{2} = \frac{(m_{1} + m_{2})}{2} [{(\frac{m_{1} v_{1}}{m_{1} + m_{2}})}^{2} + {(\frac{m_{2} v_{2}}{m_{1} + m_{2}})}^{2}] = \frac{5}{6} m v^{2}$ .

Количество теплоты, выделившейся после абсолютно неупругого удара, определяется формулой

$Q = E_{1} - E_{2} = \frac{3}{2} m v^{2} - \frac{5}{6} m v^{2} = \frac{2}{3} m v^{2}$ .

Доля механической энергии, превратившейся в теплоту в результате абсолютно неупругого удара,

$η = \frac{Q}{E_{1}} = \frac{2 m v^{2}}{3} \frac{2}{3 m v^{2}} = \frac{4}{9} \approx 0,44$ .

При абсолютно неупругом ударе двух тел с заданными соотношениями масс и скоростей в теплоту перешло около 44 % механической энергии системы.

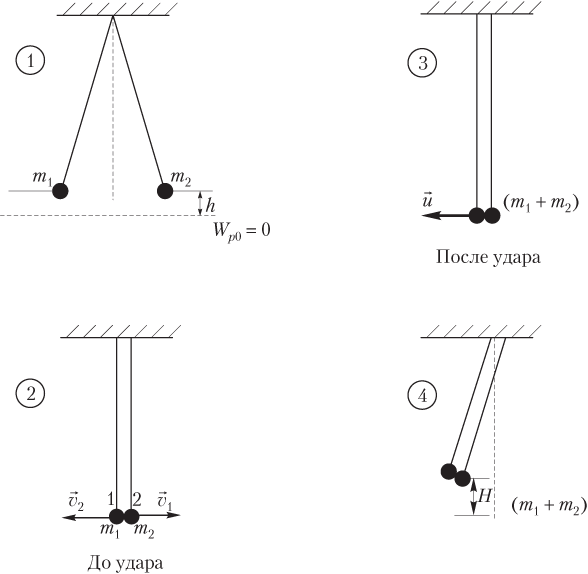
Пример 37. Два пластилиновых шарика, массы которых соотносятся как 1:5, подвешены на нитях одинаковой длины. Шарики симметрично разводят в противоположные стороны и отпускают. Какая часть механической энергии перейдет в теплоту при абсолютно неупругом ударе?

Решение. На рисунке показаны четыре состояния системы тел:

1) шарики симметрично разведены в стороны, при этом они подняты на высоту h над нулевым уровнем потенциальной энергии; полная механическая энергия системы является потенциальной:

E₁ = m₁gh + m₂gh,

или с учетом соотношения масс (m₁ = m, m₂ = 5m):

E₁ = 6mgh,

где g — модуль ускорения свободного падения; h — первоначальная высота шариков над нулевым уровнем потенциальной энергии;

2) шарики подлетают друг к другу (но соударения еще не происходит); полная механическая энергия системы является кинетической:

$E_{2} = \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2}$ ,

или с учетом соотношения масс (m₁ = m, m₂ = 5m):

$E_{2} = \frac{m}{2} (v_{1}^{2} + 5 v_{2}^{2})$ ,

где v₁ — модуль скорости первого шарика; v₂ — модуль скорости второго шарика;

3) шарики после абсолютно неупругого удара объединяются и движутся как единое целое с некоторой скоростью; полная механическая энергия системы является кинетической:

$E_{3} = \frac{(m_{1} + m_{2}) u^{2}}{2}$ ,

или с учетом соотношения масс (m₁ = m, m₂ = 5m):

E₃ = 3mu²,

где u — модуль скорости объединенного тела непосредственно после удара;

4) объединенное тело поднимается на некоторую высоту, полная механическая энергия системы является потенциальной:

E₄ = (m₁ + m₂)gH,

или с учетом соотношения масс (m₁ = m, m₂ = 5m):

E₄ = 6mgH,

где H — максимальная высота, на которую может подняться объединенное тело.

При переходе системы из первого состояния во второе полная механическая энергия сохраняется как для всей системы, так и для каждого шарика в отдельности:

$\begin{array}{l} m_{1} g h = \frac{m_{1} v_{1}^{2}}{2}; \\ m_{2} g h = \frac{m_{2} v_{2}^{2}}{2} . \end{array}}$

Отсюда следует равенство модулей скоростей шариков перед абсолютно неупругим ударом:

$v = v_{1} = v_{2} = \sqrt{2 g h}$ .

С учетом этого равенства полная механическая энергия системы перед ударом определяется формулой

E₂ = 3mv².

При переходе системы из второго состояния в третье полная механическая энергия системы не сохраняется (при абсолютно неупругом ударе часть энергии переходит в теплоту), однако импульс системы сохраняется:

$m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2} = (m_{1} + m_{2}) \vec{u}$ ,

в проекции на направление скорости объединенного тела

$- m_{1} v_{1} + m_{2} v_{2} = (m_{1} + m_{2}) u$ ,

или с учетом соотношения масс (m₁ = m, m₂ = 5m) и равенства модулей скоростей (v = v₁ = v₂):

2v = 3u.

Отсюда найдем отношение модулей скоростей шариков до и после удара:

$\frac{u}{v} = \frac{2}{3}$ .

Искомой величиной является доля механической энергии, которая перейдет в результате абсолютно неупругого удара в теплоту, т.е.

$η = \frac{Q}{E_{2}} = \frac{E_{2} - E_{3}}{E_{2}} = 1 - \frac{E_{3}}{E_{2}}$ ,

где E₂ — полная механическая энергия системы до удара (состояние 2); E₃ — полная механическая энергия системы после удара (состояние 3).

Подстановка в формулу соответствующих энергий и отношения скоростей (u/v) дает искомую долю:

$η = 1 - \frac{3 m u^{2}}{3 m v^{2}} = 1 - \frac{u^{2}}{v^{2}} = 1 - {(\frac{u}{v})}^{2} = 1 - {(\frac{2}{3})}^{2} = \frac{5}{9} \approx 0,56$ .

Таким образом, при абсолютно неупругом ударе шариков с заданным соотношением масс в теплоту превращается около 56 % их суммарной механической энергии.

Пример 38. Тело массой 2,0 кг влетает в вязкую среду со скоростью 10 м/c. Определить кинетическую энергию тела при вылете из среды, если 30 % его механической энергии в среде превращается в теплоту.

Решение. На рисунке показаны два положения тела:

1) перед попаданием в вязкую среду; тело имеет полную механическую (кинетическую) энергию E₁;

2) после вылета из вязкой среды; тело имеет полную механическую (кинетическую) энергию E₂.

Теплота, которая выделяется при движении тела в вязкой среде, определяется разностью

Q = E₁ − E₂,

где Q = 0,3E₁ — по условию задачи.

Выразим искомую кинетическую энергию тела при вылете из вязкой среды:

E₂ = E₁ − Q.

Замена Q = 0,3E₁ преобразует формулу к виду:

E₂ = E₁ − 0,3E₁ = 0,7E₁,

где $E_{1} = \frac{m v_{1}^{2}}{2}$ — кинетическая энергия тела перед его попаданием в вязкую среду; m — масса тела; v₁ — модуль первоначальной скорости тела.

Окончательная формула для расчета искомой кинетической энергии имеет следующий вид:

$E_{2} = \frac{0,7 m v_{1}^{2}}{2} = 0,35 m v_{1}^{2}$ .

Произведем вычисление:

E₂ = 0,35 ⋅ 2,0 ⋅ 10² = 70 Дж.