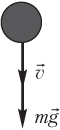Физика

Пример 20. Тело массой 60 г к моменту падения на Землю имеет скорость 5,0 м/с. Определить мощность силы тяжести в этот момент.

Решение. На рисунке показаны направления скорости тела и силы тяжести, действующей на тело.

В задаче задана мгновенная скорость тела; следовательно, мощность, которую необходимо рассчитать, также является мгновенной мощностью. Величина мгновенной мощности силы тяжести определяется формулой

N = mgv cos α,

где mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; v — модуль скорости тела; α = 0° — угол между векторами скорости и силы.

Произведем вычисление:

$N=60\cdot {10}^{-3}\cdot 10\cdot \mathrm{5,0}\cdot 1=\mathrm{3,0}$ Вт.

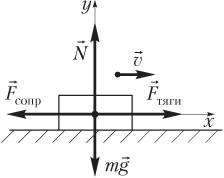
Пример 21. При скорости 36 км/ч мощность двигателя автомобиля равна 2,0 кВт. Считая, что сила сопротивления движению автомобиля со стороны воздуха и дороги пропорциональна квадрату скорости, определить мощность двигателя при скорости 72 км/ч.

Решение. Мощность двигателя автомобиля определяется силой тяги и скоростью:

$N^{\text{*}}=F_{\text{тяги}}v\cos \alpha$,

где F_тяги — величина силы тяги двигателя автомобиля; v — модуль скорости автомобиля при заданной мощности; α = 0° — угол между векторами силы тяги и скорости.

Силы, действующие на автомобиль, направление его скорости и выбранная система координат показаны на рисунке.

Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобиль движется с постоянной скоростью:

${\overrightarrow{F}}_{\text{тяги}}+{\overrightarrow{F}}_{\text{сопр}}+m\overrightarrow{g}+\overrightarrow{N}=0$,

или в проекциях на координатные оси —

$\begin{array}{l}Ox\text{: }{F}_{\text{тяги}}-F_{\text{сопр}}=0;\\ Oy\text{: }N-mg=\mathrm{0,}\end{array}\}$

где F_сопр — модуль силы сопротивления движению автомобиля; N — модуль силы нормальной реакции, действующей на автомобиль со стороны дороги; m — масса автомобиля; g — модуль ускорения свободного падения.

Из первого уравнения системы следует равенство модулей сил тяги и сопротивления:

F_тяги = F_сопр.

По условию задачи сила сопротивления пропорциональна квадрату скорости автомобиля:

F_сопр = kv²,

где k — коэффициент пропорциональности.

Подстановка данного выражения в формулу для силы тяги

F_тяги = kv²,

а затем в формулу для вычисления мощности дает:

$N^{\text{*}}=k{v}^3\cos \alpha$.

Таким образом, мощность двигателя автомобиля определяется формулой:

• при скорости v₁ —

$N_1^{\text{*}}=k{v}_1^3\cos \alpha$;

• при скорости v₂ —

$N_2^{\text{*}}=k{v}_2^3\cos \alpha$,

где v₁ = 36 км/ч — первая скорость автомобиля; v₂ = 72 км/ч — вторая скорость автомобиля.

Отношение

$\frac{N_1^{\text{*}}}{N_2^{\text{*}}}=\frac{k{v}_1^3\cos \alpha }{k{v}_2^3\cos \alpha }={\left(\frac{v_1}{v_2}\right)}^3$

позволяет вычислить искомую мощность автомобиля:

$N_2^{\text{*}}=N_1^{\text{*}}{\left(\frac{v_2}{v_1}\right)}^3=\mathrm{2,0}\cdot {10}^3\cdot {\left(\frac{72}{36}\right)}^3=16\cdot {10}^3\text{ Вт}=16$ кВт.

Пример 22. Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.

Решение. Мощность двигателей автомобилей определяется фор­мулой:

• для первого автомобиля

$N_1^{\text{*}}=F_{\text{тяги}1}{v}_1\cos \alpha$,

• для второго автомобиля

$N_2^{\text{*}}=F_{\text{тяги}2}{v}_2\cos \alpha$,

где F_тяги1 — величина силы тяги двигателя первого автомобиля; v₁ — модуль скорости первого автомобиля; F_тяги2 — величина силы тяги двигателя второго автомобиля; v₂ — модуль скорости второго автомобиля; α = 0° — угол между векторами силы тяги и скорости.

Силы, действующие на первый и второй автомобиль, направление движения и выбранная система координат показаны на рисунке.

Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобили движутся равноускоренно:

• для первого автомобиля

${\overrightarrow{F}}_{\text{тяги}1}+m_1\overrightarrow{g}+{\overrightarrow{N}}_1=m_1{\overrightarrow{a}}_1$,

или в проекциях на координатные оси —

$\begin{array}{l}Ox\text{: }{F}_{\text{тяги}1}=m_1{a}_1;\\ Oy\text{: }{N}_1-m_{1}g=\mathrm{0,}\end{array}\}$

• для второго автомобиля

${\overrightarrow{F}}_{\text{тяги}2}+m_2\overrightarrow{g}+{\overrightarrow{N}}_2=m_2{\overrightarrow{a}}_2$,

или в проекциях на координатные оси —

$\begin{array}{l}Ox\text{: }{F}_{\text{тяги}2}=m_2{a}_2;\\ Oy\text{: }{N}_2-m_{2}g=\mathrm{0,}\end{array}\}$

где m₁ — масса первого автомобиля; m₂ — масса второго автомобиля; g — модуль ускорения свободного падения; N₁ — модуль силы нормальной реакции, действующей на первый автомобиль со стороны дороги; N₂ — модуль силы нормальной реакции, действующей на второй автомобиль со стороны дороги; a₁ — модуль ускорения первого автомобиля; a₂ — модуль ускорения второго автомобиля.

Из записанных уравнений следует, что величины сил тяги первого и второго автомобиля определяются формулами:

• для первого автомобиля

F_тяги1 = m₁a₁,

• для второго автомобиля

F_тяги2 = m₂a₂.

Отношение модулей сил тяги (F_тяги1/F_тяги2) определяется отношением

$\frac{F_{\text{тяги}1}}{F_{\text{тяги}2}}=\frac{m_1{a}_1}{m_2{a}_2}$.

Движение автомобилей происходит равноускоренно без начальной скорости, поэтому их скорость с течением времени изменяется по законам:

• для первого автомобиля

v₁ = a₁t,

• для второго автомобиля

v₂ = a₂t,

где t — время.

Отношение модулей скоростей (v₁/v₂) определяется отношением величин ускорений (a₁/a₂):

$\frac{v_1}{v_2}=\frac{a_1}{a_2}$,

а отношение мощностей —

$\frac{N_1^{\text{*}}}{N_2^{\text{*}}}=\frac{F_{\text{тяги}1}{v}_1\cos \alpha }{F_{\text{тяги}2}{v}_2\cos \alpha }=\frac{F_{\text{тяги}1}}{F_{\text{тяги}2}}\frac{v_1}{v_2}.$

Подставим в полученное отношение выражения для (F_тяги1/F_тяги2) и (v₁/v₂):

$\frac{N_1^{\text{*}}}{N_2^{\text{*}}}=\frac{m_1{a}_1}{m_2{a}_2}\frac{a_1}{a_2}=\frac{m_1}{m_2}{\left(\frac{a_1}{a_2}\right)}^2$.

Преобразование формулы с учетом равенства масс автомобилей (m₁ = m₂ = m) и замены (a₁/a₂ = v₁/v₂) дает искомое отношение мощностей:

$\frac{N_1^{\text{*}}}{N_2^{\text{*}}}={\left(\frac{v_1}{v_2}\right)}^2={\left(\frac{2v_2}{v_2}\right)}^2=2^2=4$.

Таким образом, мощность первого автомобиля в 4 раза больше мощности второго автомобиля.