Предметы

Физика

Законы сохранения

3.3. Работа и мощность механической системы

3.3.1. Работа механической силы

Теория Тренинг

Физика

Общий тест

3.3. Работа и мощность механической системы

3.3.1. Работа механической силы

Сила, приложенная к телу, может совершать работу. Расчет работы силы, приложенной к телу, производится по-разному в зависимости от того, является ли сила постоянной величиной.

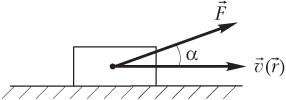
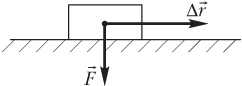
Если сила постоянна на всем перемещении тела, которое происходит под действием этой силы (рис. 3.2),

Рис. 3.2

то работа вычисляется по формуле

$A = (\vec{F}, Δ \vec{r}) = \vec{F} \cdot Δ \vec{r} = F Δ r \cos α$ ,

где α — угол между векторами $\vec{F}$ и $Δ \vec{r}$ ; $\vec{F}$ — сила, приложенная к телу; $Δ \vec{r}$ — перемещение тела.

В Международной системе единиц работа измеряется в джоулях (1 Дж).

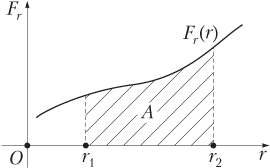
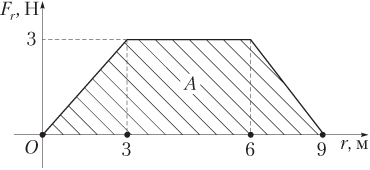
Если сила зависит от перемещения, то ее работа вычисляется графически как площадь под кривой F_r(r) (рис. 3.3). Величина F_r(r) представляет собой проекцию силы, приложенной к телу, на направление перемещения.

Рис. 3.3

Частные случаи расчета работы:

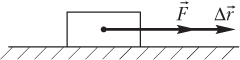
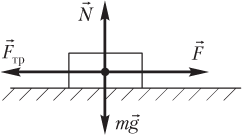
1) если направление силы $\vec{F}$ и направление перемещения $Δ \vec{r}$ совпадают (рис. 3.4), то совершается максимально возможная положительная работа:

A = F∆r cos 0° = F∆r.

Рис. 3.4

В любом случае, когда сила приложена под острым углом к перемещению, совершается положительная работа;

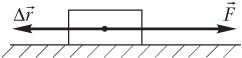
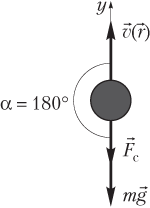
2) если направление силы $\vec{F}$ и направление перемещения $Δ \vec{r}$ противоположны (рис. 3.5), то совершается максимально возможная отрицательная работа:

A = F∆r cos 180° = −F∆r.

Рис. 3.5

В любом случае, когда сила приложена под тупым углом к перемещению, совершается отрицательная работа;

3) если направление силы $\vec{F}$ и направление перемещения $Δ \vec{r}$ взаимно перпендикулярны (рис. 3.6), то работа этой силой не совершается:

A = F∆r cos 90° = 0.

Рис. 3.6

Работа также не совершается, когда под действием силы не происходит перемещения тела по поверхности.

Пример 16. К телу массой 3,0 кг, покоящемуся на горизонтальной поверхности, в горизонтальном направлении прикладывают силу 5,0 Н. Коэффициент трения между телом и поверхностью равен 0,2. Определить работу указанной силы, совершенную за 10 с.

Решение. Силы, приложенные к телу, показаны на рисунке.

Сила $\vec{F}$ является постоянной, поэтому вычисление работы производим по формуле

A = F∆ cos α,

где F — сила, приложенная к телу в горизонтальном направлении; ∆r — модуль перемещения тела под действием указанной силы; α = 0° — угол между направлениями силы и перемещения.

Для вычисления работы по формуле, записанной выше, необходимо рассчитать перемещение за указанное в условии задачи время.

Движение тела начинается, когда величина приложенной силы превышает значение максимальной силы трения покоя:

$F \geq F_{пок}^{\max}$ ,

где $F_{пок}^{\max} = μ N = μ m g$ — модуль максимальной силы трения покоя.

Расчет дает ее величину:

$F_{тр . пок}^{\max} = 0,2 \cdot 3,0 \cdot 10 = 6,0$ Н.

Значение силы, приложенной к телу, меньше величины максимальной силы трения покоя:

$F < F_{пок}^{\max}$ ;

следовательно, тело останется в покое.

Таким образом, под действием указанной силы тело перемещаться не будет (∆r = 0). Поэтому работа этой силы равна нулю:

A = 5,0 ⋅ 0 ⋅ cos 0° = 0.

Пример 17. На тело массой 1,0 кг, брошенное с поверхности Земли вертикально вверх с начальной скоростью 12 м/с, действует постоянная сила сопротивления, равная по модулю 2,0 Н. Определить работу силы тяжести за время подъема тела до максимальной высоты.

Решение. При подъеме тела сила сопротивления его движению направлена вниз. Силы, приложенные к телу, и направление скорости тела (направление перемещения) показаны на рисунке.

Сила тяжести является постоянной величиной, поэтому вычисление ее работы производим по формуле

A = mg∆r cos α,

где mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; ∆r = H — максимальная высота подъема тела, равная модулю его перемещения; α = 180° — угол между направлениями силы тяжести и перемещения.

Для вычисления работы по записанной выше формуле необходимо рассчитать максимальную высоту подъема H. Для этого определим время подъема тела до максимальной высоты из условия:

v_y = v₀ − at_под = 0.

где v_y — проекция скорости на вертикальную ось; v₀ — модуль начальной скорости тела; a — модуль ускорения.

Отсюда следует, что время подъема тела до максимальной высоты (точка остановки) определяется отношением

$t_{под} = \frac{v_{0}}{a}$ .

Подставим полученное выражение в уравнение движения тела:

$y (t_{под}) = v_{0} t_{под} - \frac{a t_{под}^{2}}{2} = \frac{v_{0}^{2}}{2 a}$ .

Таким образом, максимальная высота подъема определяется формулой

$H = \frac{v_{0}^{2}}{2 a}$ .

Для определения модуля ускорения запишем второй закон Ньютона в проекции на ось, направленную вертикально вверх:

−mg − F_сопр = −ma.

Отсюда следует, что модуль ускорения определяется отношением:

$a = \frac{m g + F_{сопр}}{m}$ ,

где F_сопр — модуль силы сопротивления.

Подстановка данного выражения в формулу для расчета максимальной высоты

$H = \frac{m v_{0}^{2}}{2 (m g + F_{сопр})}$ ,

а затем в формулу для вычисления работы дает результат:

$A = - \frac{g m^{2} v_{0}^{2}}{2 (m g + F_{сопр})} = - \frac{10 {(1,0)}^{2} \cdot 12^{2}}{2 (1,0 \cdot 10 + 2, 0)} = - 60$ Дж.

Пример 18. График зависимости проекции силы на направление перемещения от пройденного пути имеет вид трапеции с вершинами в точках (0,0), (3,3), (6,3) и (9,0), где пройденный путь задан в метрах, проекция силы — в ньютонах. Определить работу этой силы за время прохождения 9,0 м пути.

Решение. График зависимости проекции силы на направление перемещения от пройденного пути показан на рисунке.

Сила, под действием которой происходит движение тела, не является постоянной величиной, поэтому работа указанной силы вычисляется как площадь трапеции по формуле

$A = \frac{(6 - 3) + 9}{2} (3 - 0) = 18$ Дж.

Пример 19. Однородный стержень длиной 1,6 м и площадью сечения 1,0 см² плавает в воде в вертикальном положении, погрузившись на 3/4 своей длины. Какую минимальную работу нужно совершить, чтобы утопить стержень, оставляя его при этом в вертикальном положении? Плотность воды равна 1,0 г/см³.

Решение. Сила, под действием которой происходит погружение стержня в воду, не является постоянной величиной; она зависит от действующей на стержень подъемной силы, которая, в свою очередь, определяется объемом погруженной части стержня. Расчет искомой работы будем производить графически.

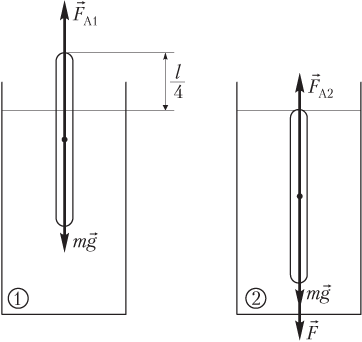
Для этого на рисунке изобразим силы, действующие на стержень, в ситуациях, когда

стержень плавает под действием двух сил: силы Архимеда ${\vec{F}}_{A 1}$ и силы тяжести $m \vec{g}$ ; модули сил равны, поэтому подъемная сила не действует:

F_под1 = F_A1 − mg = 0;

стержень удерживается под водой силой F, равной по величине подъемной силе и приложенной в противоположном направлении:

F = F_под2 = F_A2 − mg,

где m — масса стержня; g — модуль ускорения свободного падения; F_A1 = ρ₀gV₁ — модуль силы Архимеда, действующей на стержень, плавающий в воде; ρ₀ — плотность воды; $V_{1} = \frac{3}{4} V$ — объем погруженной части плавающего стержня; F_A2 = ρ₀gV₂ — модуль силы Архимеда, действующей на стержень, полностью погруженный в воду; V₂ = V = lS — объем стержня; l — длина стержня; S — площадь поперечного сечения стержня.

Установим зависимость величины силы, под действием которой происходит погружение стержня в воду, от глубины дополнительного погружения F(x). Для этого определим

значение силы F при разных значениях x;
вид зависимости F(x).

1. Найдем значение силы F в двух ситуациях:

когда стержень плавает (величина x = 0)

$F_{0} = F_{под 1} = ρ_{0} g V_{1} - m g = 0$ ,

когда стержень полностью погружен в воду (величина $x = \frac{1}{4} l$ )

$F = F_{под 2} = ρ_{0} g V_{2} - m g$ .

Преобразуем последнее равенство, подставляя объемы V₁ и V₂ в систему уравнений:

$\begin{array}{l} 0 = ρ_{0} g V_{1} - m g; \\ F = ρ_{0} g V_{2} - m g, \end{array}}$

т.е.

$\begin{array}{l} m g = \frac{3}{4} ρ_{0} g V; \\ F = ρ_{0} g V - m g . \end{array}}$

Подстановка первого уравнения системы во второе дает выражение для F:

$F = ρ_{0} g V - \frac{3}{4} ρ_{0} g V = \frac{1}{4} ρ_{0} g V = \frac{1}{3} m g$ .

Таким образом, график зависимости F(x) проходит через точки: (0 м; 0 Н) и $(\frac{l}{4} м; \frac{m g}{3} Н)$ .

2. Покажем, что зависимость F(x) является линейной.

Для дополнительного погружения плавающего стержня на глубину x к нему следует приложить силу, величина которой определяется формулой

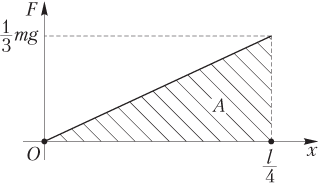
$F (x) = F_{под} = F_{A 1} + ρ_{0} g x S - m g = F_{под 1} + ρ_{0} g x S = ρ_{0} g x S$ .

Изобразим данную зависимость F(x) на рисунке в виде прямой, проходящей через указанные точки, и рассчитаем работу по погружению стержня как площадь треугольника:

$A = \frac{1}{2} \cdot \frac{1}{3} m g \frac{l}{4} = \frac{m g l}{24}$ .

Величина силы тяжести (mg) может быть определена из равенства

$m g = ρ_{0} g V_{1} = \frac{3}{4} ρ_{0} g l S$ .

Таким образом, для полного погружения стержня необходимо совершить минимальную работу, определяемую формулой

$A = \frac{m g l}{24} = \frac{3}{24 \cdot 4} ρ_{0} g l^{2} S = \frac{ρ_{0} g l^{2} S}{32}$ .

Расчет дает значение:

$A = \frac{1,0 \cdot 10^{3} \cdot 10 \cdot {(1,6)}^{2} \cdot 1,0 \cdot 10^{- 4}}{32} = 0,08 Дж = 80$ мДж.