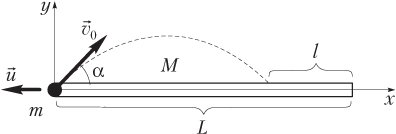Предметы

Физика

Законы сохранения

3.2. Импульс

3.2.5. Закон сохранения импульса

Теория Тренинг

Физика

Общий тест

3.2. Импульс

3.2.5. Закон сохранения импульса

Если импульс равнодействующей всех сил, действующих на тело, равен нулю, то импульс тела сохраняется. Это утверждение носит название закона сохранения импульса и записывается в виде:

$Δ \vec{P} = 0$ , или ${\vec{P}}_{2} = {\vec{P}}_{1}$ ,

где ${\vec{P}}_{1} = m {\vec{v}}_{1}$ — начальный импульс тела; ${\vec{P}}_{2} = m {\vec{v}}_{2}$ — его конечный импульс.

Если одна из проекций импульса равнодействующей всех сил, действующих на тело (например, на ось Ox), равна нулю

I_x = 0,

то сохраняется соответствующая проекция импульса:

∆P_x = 0, или P_x₂ = P_x₁,

где P_x₁ = mv_x₁ — проекция начального импульса тела на ось Ox; P_x₂ = = mv_x₂ — проекция конечного импульса тела на указанную ось; m — масса тела; v_x₁ и v_x₂ — проекции начальной и конечной скоростей на ось Ox.

Это утверждение носит название закона сохранения проекции импульса.

Импульс сохраняется при любых видах столкновений тел (абсолютно упругих, неупругих, абсолютно неупругих):

$\sum \vec{P} = 0$ , или ${\vec{P}}_{2} = {\vec{P}}_{1}$ ,

где P₁ — импульс системы до взаимодействия, P₂ — импульс системы после взаимодействия.

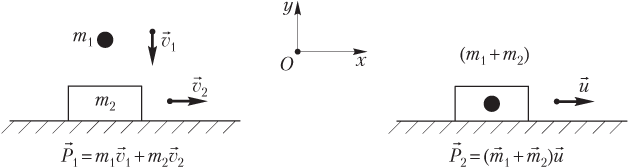
Пример 10. В тележку с песком, движущуюся по горизонтальной поверхности со скоростью 5,5 м/с, попадает вертикально падающее тело и застревает в песке. Определить скорость тележки после попадания тела в песок. Масса падающего тела в 10 раз меньше массы тележки.

Решение. В данной ситуации сохраняется только x-составляющая импульса системы тело — тележка, y-составляющая импульса системы не сохраняется:

${\vec{P}}_{1 x} = {\vec{P}}_{2 x}$ , ${\vec{P}}_{1 y} \neq {\vec{P}}_{2 y}$ ,

где ${\vec{P}}_{1} = m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2}$ — импульс системы до попадания пули в песок; ${\vec{P}}_{2} = (m_{1} + m_{2}) \vec{u}$ — импульс системы после застревания тела в песке; m₁ — масса тела; m₂ — масса тележки; ${\vec{v}}_{1}$ — скорость тела непосредственно перед его попаданием в песок; ${\vec{v}}_{2}$ — скорость тележки; $\vec{u}$ — скорость тележки с застрявшим в песке телом.

На рисунке показаны скорости тела и тележки, а также выбранная система координат.

Запишем закон сохранения импульса системы тело — тележка для оси Ox:

P₁_x = P₂_x,

или в явном виде:

m₂v₂ = (m₁ + m₂)u.

С учетом соотношения масс тела и тележки

m₂ = 10m₁

записанный закон приобретает вид:

10m₁v₂ = (m₁ + 10m₁)u,

или

10v₂ = 11u.

Отсюда — искомая скорость тележки после попадания в нее тела:

$u = \frac{10}{11} v_{2}$ ,

что после расчета дает значение:

$u = \frac{10}{11} \cdot 5,5 = 5,0$ м/с.

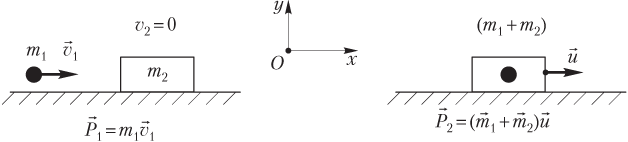
Пример 11. Снаряд массой 25,0 кг, летящий горизонтально со скоростью 800 м/с, попадает в платформу и застревает в ней. Масса платформы 775 кг. Определить скорость, с которой начнет двигаться платформа после попадания в нее снаряда, если скорость снаряда направлена вдоль железнодорожного полотна.

Решение. В данной ситуации импульс системы снаряд — платформа сохраняется:

${\vec{P}}_{1} = {\vec{P}}_{2}$ ,

где ${\vec{P}}_{1} = m_{1} {\vec{v}}_{1}$ — импульс системы до попадания снаряда в платформу; ${\vec{P}}_{2} = (m_{1} + m_{2}) \vec{u}$ — импульс системы после попадания снаряда в платформу; m₁ — масса снаряда; m₂ — масса платформы; ${\vec{v}}_{1}$ — скорость снаряда непосредственно перед его попаданием в платформу; $\vec{u}$ — скорость платформы с застрявшим в ней снарядом.

На рисунке показаны скорости снаряда и платформы, а также выбранная система координат.

Запишем закон сохранения импульса системы снаряд — платформа в явном виде:

m₁v₁ = (m₁ + m₂)u.

Отсюда — искомая скорость платформы после попадания в нее снаряда:

$u = \frac{m_{1} v_{1}}{(m_{1} + m_{2})}$ .

Произведя вычисление, получим значение:

$u = \frac{25,0}{25,0 + 775} \cdot 800 = 25$ м/с.

Пример 12. Лягушка массой 0,10 кг сидит на конце доски, имеющей массу 4,2 кг и длину 1,0 м. Под каким углом в градусах должна прыгнуть лягушка, чтобы оказаться на другом конце доски? Известно, что лягушка совершает прыжок с начальной скоростью 5,0 м/с относительно воды в пруду. Трением доски о воду пренебречь.

Решение. Инерциальную систему отсчета (ИСО) свяжем с водой в пруду.

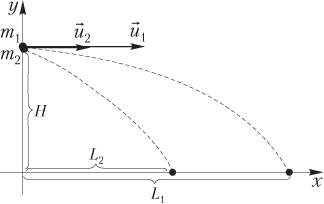
Проиллюстрируем условие задачи рисунком:

доска длиной L расположена вдоль оси Ox системы координат, начало которой совпадает с тем концом доски, на котором сидит лягушка;
лягушка массой m выполняет прыжок из начала системы координат под углом α к положительному направлению оси Ox с начальной скоростью ${\vec{v}}_{0}$ ;
при прыжке лягушки доска массой M испытывает отдачу — движется равномерно со скоростью $\vec{u}$ в отрицательном направлении оси Ox — и за время «полета» лягушки отплывает на расстояние l.

Для того чтобы приземлиться на конце доски, лягушка должна прыгнуть на расстояние

L − l = v₀t₀ cos α,

где t₀ — время полета лягушки; l = ut₀ — расстояние, на которое переместилась доска за время t₀.

Таким образом, дальность полета лягушки определяется формулой

L − ut₀ = v₀t₀ cos α.

Величину скорости движения доски u найдем из закона сохранения x-проекции импульса системы доска — лягушка:

P₁_x = P₂_x,

где P₁_x = 0 — x-проекция импульса системы до прыжка лягушки; $P_{2 x} = (m v_{0} \cos α - M u)$ — x-проекция импульса системы после прыжка лягушки.

Явный вид приведенного равенства:

$m v_{0} \cos α - M u = 0$ , или $M u = m v_{0} \cos α$ .

Время полета t₀ лягушки определяется из условия обращения в ноль y-координаты лягушки в указанный момент времени: y(t₀) = 0, или в явном виде:

$v_{0} t_{0} \sin α - \frac{g t_{0}^{2}}{2} = 0$ ,

где g — модуль ускорения свободного падения.

Решение системы уравнений

$\begin{array}{l} L - u t_{0} = v_{0} t_{0} \cos α, \\ M u = m v_{0} \cos α, \\ v_{0} t_{0} \sin α - \frac{g t_{0}^{2}}{2} = 0 \end{array}}$

дает выражение для вычисления угла α:

$\sin 2 α = \frac{L M g}{v_{0}^{2} (M + m)} = \frac{1,0 \cdot 4,2 \cdot 10}{{5,0}^{2} (4,2 + 0,1)} \approx 0,3907$ .

Искомый угол составляет

$α = \frac{1}{2} arcsin (0,3907) \approx 12 °$ .

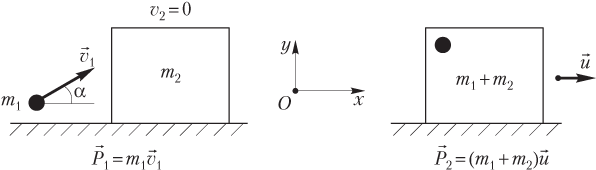
Пример 13. На гладком горизонтальном столе лежит брусок массой 2,0 кг. Пуля массой 9,0 г, летящая со скоростью 800 м/c, в тот момент, когда ее скорость направлена под углом 30° к горизонту, попадает в брусок и застревает в нем. С какой скоростью и в каком направлении стал двигаться брусок?

Решение. В данной ситуации сохраняется только x-составляющая импульса системы пуля — брусок, y-составляющая не сохраняется:

${\vec{P}}_{1 x} = {\vec{P}}_{2 x}$ , ${\vec{P}}_{1 y} \neq {\vec{P}}_{2 y}$ ,

где ${\vec{P}}_{1} = m_{1} {\vec{v}}_{1}$ — импульс системы до попадания пули в брусок; ${\vec{P}}_{2} = (m_{1} + m_{2}) \vec{u}$ — импульс системы после застревания пули в бруске; m₁ — масса пули; m₂ — масса бруска; ${\vec{v}}_{1}$ — скорость пули непосредственно перед ее попаданием в брусок; $\vec{u}$ — скорость бруска с застрявшей в нем пулей.

На рисунке показаны скорости пули и бруска, а также выбранная система координат.

Запишем закон сохранения импульса системы пуля — брусок для оси Ox:

P₁_x = P₂_x

в явном виде:

$m_{1} v_{1} \cos α = (m_{1} + m_{2}) u$ .

Отсюда — искомая скорость бруска после попадания в него пули:

$u = \frac{m_{1} v_{1} \cos α}{(m_{1} + m_{2})}$ .

Расчет дает значение:

$u = \frac{9,0 \cdot 10^{- 3} \cdot 800 \cdot 0,5 \sqrt{3}}{9,0 \cdot 10^{- 3} + 2,0} \cdot 800 \approx 3,1$ м/с.

Брусок с застрявшей в нем пулей движется со скоростью 3,1 м/с в горизонтальном направлении.

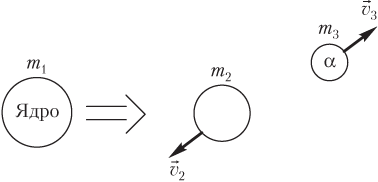
Пример 14. Ядро радона с атомной массой 216 выбрасывает α-частицу с атомной массой 4. Во сколько раз скорость α-частицы превышает скорость ядра, образовавшегося в результате испускания α-частицы?

Решение. При испускании α-частицы ядро радона претерпевает изменение: оно превращается в ядро другого элемента с атомной массой, на 4 атомные единицы меньшей первоначального значения:

A₂ = A₁ − A₃ = 216 − 4 = 212,

где A₁ = 216 — атомная масса (массовое число) радона; A₃ = 4 — атомная масса (массовое число) α-частицы.

Импульс системы ядро — α-частица сохраняется:

${\vec{P}}_{1} = {\vec{P}}_{2}$ ,

где ${\vec{P}}_{1} = 0$ — импульс ядра радона до испускания α-частицы; ${\vec{P}}_{2} = m_{2} {\vec{v}}_{2} + m_{3} {\vec{v}}_{3}$ — импульс системы после испускания ядром радона α-частицы; $m_{2} {\vec{v}}_{2}$ — импульс ядра, образовавшегося из ядра радона в результате испускания α-частицы; m₂ — масса образовавшегося ядра; ${\vec{v}}_{2}$ — скорость образовавшегося ядра; $m_{3} {\vec{v}}_{3}$ — импульс α-частицы; m₃ — масса α-частицы; ${\vec{v}}_{3}$ — скорость α-частицы.

На рисунке показаны скорости образовавшегося ядра и α-частицы.

Запишем закон сохранения импульса для системы ядро — α-частица в явном виде:

$m_{2} {\vec{v}}_{2} + m_{3} {\vec{v}}_{3} = 0$ .

Направления скоростей движения образовавшегося ядра и α-частицы противоположны. Следовательно, в проекции на направление движения α-частицы закон сохранения импульса имеет вид:

$m_{3} v_{3} - m_{2} v_{2} = 0$ .

Отсюда — искомое отношение скоростей:

$\frac{v_{3}}{v_{2}} = \frac{m_{2}}{m_{3}}$ .

Заменим отношение масс образовавшегося ядра и α-частицы (m₂/m₃) соответствующим отношением массовых чисел (A₂/A₃):

$\frac{v_{3}}{v_{2}} = \frac{A_{2}}{A_{3}}$ .

Произведя вычисление, получим значение:

$\frac{v_{3}}{v_{2}} = \frac{212}{4} = 53$ .

Таким образом, скорость испущенной α-частицы в 53 раза превышает скорость ядра, образовавшегося при ее испускании.

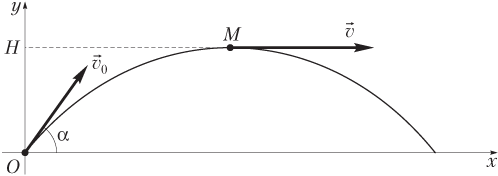
Пример 15. Снаряд массой M, выпущенный из орудия со скоростью v₀ под углом α к горизонту, взрывается в верхней точке траектории и распадается на два осколка. Масса первого осколка составляет m₁, а его скорость сразу после взрыва равна u₁ и направлена так же, как и скорость снаряда в момент взрыва. Найти расстояние L, на котором друг от друга осколки упадут на Землю.

Решение. В момент взрыва скорости снаряда и осколков направлены следующим образом:

скорость снаряда $\vec{v}$ направлена горизонтально, ее модуль определяется выражением

v = v₀ cos α;

скорость первого осколка ${\vec{u}}_{1}$ направлена в положительном направлении оси Ox;
скорость второго осколка ${\vec{u}}_{2}$ может быть направлена как в положительном, так и в отрицательном направлении оси Ox.

Скорости снаряда (начальная скорость ${\vec{v}}_{0}$ и скорость в момент взрыва $\vec{v}$ ) и система координат показаны на рисунке.

Закон сохранения импульса системы снаряд — осколки в проекции на ось Ox

P_x = P₁_x + P₂_x

запишем в виде:

$M v_{0} \cos α = m_{1} u_{1} + m_{2} u_{2 x}$ ,

где P_x = Mv₀ cos α — проекция на указанную ось импульса снаряда в точке взрыва; P₁_x = m₁u₁ — проекция импульса первого осколка; P₂_x = m₂u₂_x — проекция импульса второго осколка; M — масса снаряда; v₀ — модуль начальной скорости снаряда; α — угол, который составляет начальная скорость снаряда с горизонтом; m₁ — масса первого осколка; u₁ — модуль скорости первого осколка; m₂ — масса второго осколка; u₂_x — проекция скорости второго осколка на указанную ось.

Из записанного равенства выразим x-проекцию скорости второго осколка:

$u_{2 x} = \frac{M v_{0} \cos α - m_{1} u_{1}}{m_{2}}$ .

Значение проекции определяется конкретными значениями масс и скоростей; знак проекции скорости второго осколка может быть как положительным, так и отрицательным.

Запишем уравнения движения в проекциях на координатные оси:

для первого осколка

$\begin{array}{l} x_{1} (t) = u_{1} t; \\ y_{1} (t) = H - \frac{g t^{2}}{2}; \end{array}}$

для второго осколка

$\begin{array}{l} x_{2} (t) = u_{2 x} t; \\ y_{2} (t) = H - \frac{g t^{2}}{2}, \end{array}}$

где H — высота, на которой произошел взрыв снаряда; g — модуль ускорения свободного падения.

Для нахождения максимальной высоты подъема снаряда запишем y-проекцию скорости снаряда и уравнение его движения для оси Oy:

$\begin{array}{l} v_{y} (t) = v_{0} \sin α - g t; \\ y (t) = v_{0} t \sin α - \frac{g t^{2}}{2} . \end{array}}$

Данная система позволяет найти максимальную высоту подъема снаряда:

$H = \frac{v_{0}^{2} \sin^{2} α}{2 g}$ .

Время полета каждого из осколков найдем из y-уравнений движения:

$\begin{array}{l} y_{1} (t_{1 пол}) = H - \frac{g t_{1 пол}^{2}}{2} = 0; \\ y_{2} (t_{2 пол}) = H - \frac{g t_{2 пол}^{2}}{2} = 0. \end{array}}$

Отсюда следует, что время полета первого осколка совпадает с временем полета второго осколка:

$t_{1 пол} = t_{2 пол} = t_{пол} = \sqrt{\frac{2 H}{g}}$ .

C учетом выражения для максимальной высоты подъема получим формулу, определяющую время полета, в явном виде:

$t_{пол} = \frac{v_{0} \sin α}{g}$ .

Дальность полета каждого из осколков найдем из x-уравнений движения:

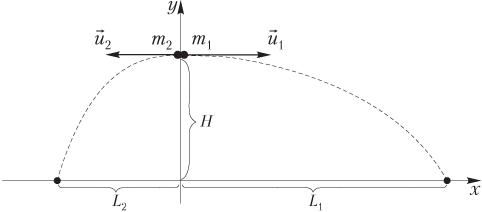
$\begin{array}{l} x_{1} (t_{1 пол}) = u_{1} t_{1 пол} = u_{1} \frac{v_{0} \sin α}{g} = L_{1}; \\ x_{2} (t_{2 пол}) = | u_{2 x} | t_{2 пол} = | u_{2 x} | \frac{v_{0} \sin α}{g} = L_{2} . \end{array}}$

Расстояние между осколками находится по-разному в зависимости от знака проекции скорости u₂_x:

если проекция скорости имеет положительный знак, то второй осколок летит в ту же сторону, что и снаряд в момент взрыва; расстояние между осколками рассчитывается как разность:

$Δ L = | L_{1} - L_{2} |$ ;

если проекция скорости имеет отрицательный знак, то второй осколок летит в сторону, противоположную скорости снаряда во время взрыва; расстояние между осколками рассчитывается как сумма:

∆L = L₁ + L₂.