Физика

В 1913 г. Н. Бор предложил новую модель атома и сформулировал принципиально новые положения, отражающие квантовый характер происходящих процессов, — постулаты Бора.

Согласно первому постулату Бора ( постулату стационарных состояний) атомная система может находиться только в стационарных (неизменяющихся во времени) состояниях, каждому из которых соответствует определенное дискретное значение энергии; в стационарном состоянии атом не излучает электромагнитные волны.

В стационарном состоянии энергия электрона в атоме квантуется, т.е. принимает ряд дискретных (определенных) значений, определяемых формулой

$E_n=-\frac{k^2{Z}^2{e}^{4}m}{2{\hslash }^2{n}^2}$,

где k = 1/4πε₀ ≈ 9 ⋅ 10⁹ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Ф/м; Z — зарядовое число; e — заряд электрона, e = = −1,6 ⋅ 10⁻¹⁹ Кл; m — масса электрона, m = 9,11 ⋅ 10⁻³¹ кг; ℏ — приведенная постоянная Планка, ℏ = h/2π = 1,055 ⋅ 10⁻³⁴ Дж ⋅ с; h — постоянная Планка, h = 6,626 ⋅ 10⁻³⁴ Дж ⋅ с; n — главное квантовое число.

Главное квантовое число n принимает ряд натуральных значений:

1) значение n = 1 соответствует основному состоянию электрона в водородоподобном атоме; энергия основного состояния определяется формулой

$E_1=-\frac{k^2{Z}^2{e}^{4}m}{2{\hslash }^2}$,

где Z — порядковый номер химического элемента в Периодической системе элементов Д.И. Менделеева; для атома водорода (Z = 1) значение энергии основного состояния равно:

$E_1\left({}_1{}^1\text{H}\right)=-\frac{k^2{e}^{4}m}{2{\hslash }^2}=-\mathrm{13,6}$ эВ;

2) значения n = 2, 3, … соответствуют возбужденным состояниям электрона в водородоподобном атоме.

Для упрощения вычислений энергии n-го состояния электрона в атоме применяют формулу

$E\left(\text{эВ}\right)=-\mathrm{13,6}\cdot \frac{Z^2}{n^2}$,

где E(эВ) — значение энергии в электронвольтах; n = 1, 2, 3, … — главное квантовое число.

Полная энергия электрона в атоме согласно модели Резерфорда (планетарной модели) определяется формулой

$E_{\text{полн}}=-\frac{kZ{e}^2}{2r}$,

где k = 1/4πε₀ ≈ 9 ⋅ 10⁹ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Ф/м; Z|e| — заряд ядра; Z — зарядовое число; e — заряд электрона, e = −1,6 ⋅ 10⁻¹⁹ Кл; r — радиус орбиты электрона.

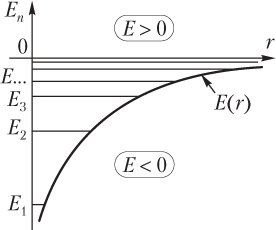
На рис. 13.15 показана соответствующая зависимость E(r).

Согласно модели Бора (квантовой модели) полная энергия электрона в атоме определяется формулой

$E_n=-\frac{k^2{Z}^2{e}^{4}m}{2{\hslash }^2{n}^2}$,

где ℏ — приведенная постоянная Планка, ℏ = h/2π ≈ 1,055 ⋅ 10⁻³⁴ Дж ⋅ с; h — постоянная Планка, h = 6,626 ⋅ 10⁻³⁴ Дж ⋅ с; n — главное квантовое число.

На рис. 13.15 соответствующие уровни энергии показаны горизонтальными линиями.

Знак энергии электрона определяется его состоянием:

• при E < 0 электрон находится в связанном состоянии, т.е. в атоме;
• при E > 0 электрон свободен, т.е. он удален от ядра на расстояние, на котором действием кулоновских сил можно пренебречь;
• при E = 0 имеет место ионизация атома, т.е. «отрыв» электрона от атома (или захват электрона положительным ионом и образование нейтрального атома).

Энергия ионизации атома — работа, которую необходимо совершить, чтобы «оторвать» электрон от атома, т.е. перевести атом в область ионизации (E = 0).

Энергия ионизации равна разности энергий электрона в атоме (рис. 13.16):

E _i = E ₂ − E ₁,

где E ₁ — энергия начального состояния электрона в атоме, равная энергии того состояния, в котором находится электрон, E ₁ = E _n ; E ₂ — энергия конечного состояния, равная нулю, E ₂ = 0.

Энергия ионизации равна модулю энергии состояния, в котором находится электрон в атоме:

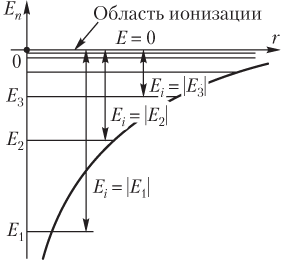
E _i = |E _n |;

является положительной величиной.

Энергия электрона в атоме:

• квантуется, т.е. принимает ряд дискретных значений (энергетический спектр атома является дискретным);
• всегда отрицательна;
• обратно пропорциональна квадрату главного квантового числа;
• возрастает с увеличением номера главного квантового числа;
• минимальна, когда электрон находится в основном энергетическом состоянии (n = 1);
• увеличивается при переходе электрона в возбужденное состояние (n = 2, 3, 4, …);
• максимальна (E = 0), когда атом находится в области ионизации;
• с увеличением номера главного квантового числа возрастает таким образом, что расстояние между двумя соседними энергетическими уровнями уменьшается;
• при больших значениях главного квантового числа (n → ∞) энергетический спектр атома становится сплошным (т.е. значения энергии двух соседних энергетических уровней практически не отличаются друг от друга).