Репетитор-онлайн — подготовка к ЦТ

13.6. Атом по теории Резерфорда

13.6.2. Строение атома (планетарная модель)

Планетарная модель атома предложена Э. Резерфордом в 1911 г.

Согласно планетарной модели атома (рис. 13.14):

в центре атома находится положительно заряженное ядро, размер которого составляет ~10⁻¹² см;
вокруг ядра по круговой орбите радиусом r движется отрицательно заряженный электрон со скоростью $\vec{v}$ ;
масса атома практически полностью сосредоточена в ядре;
движение электрона вокруг ядра происходит под действием кулоновской силы;
атом электрически нейтрален.

Планетарная модель позволяет рассчитать ряд характеристик электрона в водородоподобном атоме, исходя из следующих соображений.

1. Движение электрона вокруг ядра происходит под действием кулоновской силы ${\vec{F}}_{кул}$ , модуль которой определяется законом Кулона:

$F_{кул} = \frac{k Z e^{2}}{r^{2}}$ ,

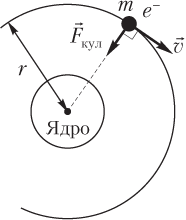Рис. 13.14

где k = 1/4πε₀ = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Ф/м; Z|e| — заряд ядра; Z — зарядовое число; e — заряд электрона, e = −1,6 ⋅ 10⁻¹⁹ Кл; r — радиус орбиты электрона.

2. Кулоновская сила является силой притяжения и направлена к центру ядра, т.е. является центростремительной силой:

F _кул = F _ц.с.

3. Величина центростремительной силы определяется формулой

$F_{ц . с} = \frac{m v^{2}}{r}$ ,

где m — масса электрона, m = 9,11 ⋅ 10⁻³¹ кг; v — модуль скорости электрона.

Записанные выше формулы образуют полную систему уравнений, позволяющую рассчитать ряд характеристик электрона в водородоподобном атоме.

Энергия электрона в атоме складывается из кинетической (энергии движения) и потенциальной (энергии взаимодействия электрона с ядром):

E _полн = W _k + W _p,

где W _k — кинетическая энергия, W _k = mv ²/2; m — масса электрона, m = 9,11 ⋅ 10⁻³¹ кг; v — модуль скорости электрона; W _p — потенциальная энергия.

Потенциальная энергия электрона в атоме является энергией взаимодействия электрона с ядром и соответствует притяжению, так как заряды ядра и электрона имеют разные знаки; поэтому потенциальная энергия отрицательна и определяется формулой

$W_{p} = - \frac{k Z e^{2}}{r} < 0$ ,

где k = 1/4πε₀ ≈ 9 ⋅ 10⁹ Н ⋅ м²/Кл²; ε₀ — электрическая постоянная, ε₀ = 8,85 ⋅ 10⁻¹² Ф/м; Z|e| — заряд ядра; Z — зарядовое число; e — заряд электрона, e = −1,6 ⋅ 10⁻¹⁹ Кл; r — радиус орбиты электрона.

Кинетическая энергия электрона в атоме является положительной величиной и определяется формулой

$W_{k} = \frac{k Z e^{2}}{2 r} > 0$ .

Полная энергия электрона в атоме является суммой потенциальной и кинетической энергий и рассчитывается по формуле

$E_{полн} = W_{k} + W_{p} = - \frac{k Z e^{2}}{2 r}$ .

Для облегчения запоминания формул для расчета энергии электрона в атоме следует помнить:

потенциальная энергия является отрицательной величиной, кинетическая — положительной;
по абсолютному значению потенциальная энергия в 2 раза превышает кинетическую;
полная энергия имеет тот же знак, что и потенциальная (знак «минус»), а ее абсолютное значение совпадает со значением кинетической.

Пример 18. Сила кулоновского взаимодействия электрона в атоме водорода с его ядром равна 1,4 ⋅ 10⁻⁸ Н. Масса электрона составляет 9,1 ⋅ 10⁻³¹ кг, а зарядовое число водорода — 1. Рассчитать скорость движения электрона по орбите.

Решение. Движение электрона вокруг ядра атома водорода происходит под действием кулоновской силы ${\vec{F}}_{кул}$ , модуль которой определяется законом Кулона:

$F_{кул} = \frac{k Z e^{2}}{r^{2}}$ ,

где k = 9,0 ⋅ 10⁹ Н ⋅ м²/Кл²; Z — зарядовое число водорода, Z = 1; e — заряд электрона, e = −1,6 ⋅ 10⁻¹⁹ Кл; r — радиус орбиты электрона.

Кулоновская сила является силой притяжения и направлена к центру ядра, т.е. является центростремительной силой, модуль которой определяется формулой

$F_{ц . с} = \frac{m v^{2}}{r}$ ,

где m — масса электрона, m = 9,1 ⋅ 10⁻³¹ кг; v — модуль скорости электрона; r — радиус орбиты электрона.

Подстановка выражений для F _кул и F _ц.с (с учетом Z = 1) в равенство

F _кул = F _ц.с

дает

$\frac{k e^{2}}{r} = m v^{2}$ .

Выразим отсюда радиус орбиты

$r = \frac{k e^{2}}{m v^{2}}$

и подставим его в выражение для кулоновской силы:

$F_{кул} = \frac{k e^{2} {(m v^{2})}^{2}}{{(k e^{2})}^{2}} = \frac{m^{2} v^{4}}{k e^{2}}$ .

Из полученного равенства выразим искомую скорость

$v = \sqrt[4]{\frac{F_{кул} k e^{2}}{m^{2}}}$ ,

где F _кул — кулоновская сила взаимодействия ядра и электрона, F _кул = = 1,4 ⋅ 10⁻⁸ Н.

Рассчитаем значение скорости электрона на данной орбите:

$v = \sqrt[4]{\frac{1,4 \cdot 10^{- 8} \cdot 9,0 \cdot 10^{9} \cdot {(- 1,6 \cdot 10^{- 19})}^{2}}{{(9,1 \cdot 10^{- 31})}^{2}}} = 1,4 \cdot 10^{6}$ м/с.

Следовательно, по данной орбите электрон движется со скоростью 1,4 ⋅ 10⁶ м/с.

Физика