Физика

Некоторые ядра являются нестабильными и самопроизвольно распадаются с течением времени, превращаясь в ядра других элементов. Такой распад называется радиоактивным.

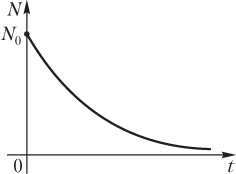
Закон радиоактивного распада: число радиоактивных (нераспавшихся) ядер с течением времени убывает по экспоненциальному закону:

N = N ₀e ^{−λ t} ,

где N — число радиоактивных (нераспавшихся) ядер к моменту времени t; N ₀ — первоначальное количество радиоактивных ядер; λ — постоянная распада (характеристика данного радиоактивного элемента).

График зависимости числа радиоактивных ядер от времени N(t) приведен на рис. 13.8.

Указанный закон может быть записан в другом виде:

$N=N_0{2}^{-\frac{t}{T_{1/2}}}$,

где T _1/2 — период полураспада радиоактивного элемента.

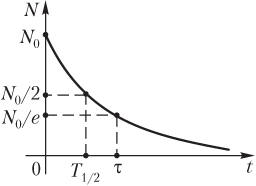
Каждый радиоактивный элемент характеризуется периодом полураспада (T _1/2), средним временем жизни (τ) и постоянной распада (λ).

Период полураспада радиоактивного элемента — время, за которое число радиоактивных ядер убывает вдвое.

Среднее время жизни — время, за которое число радиоактивных ядер убывает в e раз (e — основание натурального логарифма, e = 2,72).

На рис. 13.9 показан график зависимости числа радиоактивных ядер от времени. На графике отмечены моменты времени, соответствующие периоду полураспада и среднему времени жизни радиоактивного изотопа, и соответствующие им количества ядер.

Постоянная распада также является характеристикой данного радиоактивного элемента (справочной величиной); она связана с периодом полураспада и средним временем жизни следующими формулами:

• с периодом полураспада —

$T_{1/2}=\frac{\ln 2}{\lambda }=\frac{\mathrm{0,693}}{\lambda }$;

• со средним временем жизни —

$\tau =\frac{1}{\lambda }$.

В Международной системе единиц период полураспада и среднее время жизни измеряются в секундах (1 с), постоянная распада — в обратных секундах (1 с⁻¹).

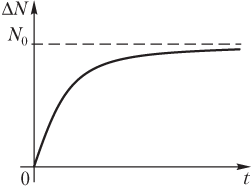
Число ядер, распавшихся к моменту времени t, определяется выражением

$\Delta N=N_0-N=N_0(1-e^{-\lambda t})$,

где ΔN — число ядер, распавшихся за промежуток времени Δt = t − t ₀, ΔN = = N ₀ − N; t ₀ — начальный момент времени, t ₀ = 0; N — число нераспавшихся (радиоактивных) ядер к моменту времени t; N ₀ — первоначальное количество радиоактивных ядер; λ — постоянная распада.

График зависимости числа ядер, распавшихся к моменту времени t, от времени ΔN(t) приведен на рис. 13.10.

Скорость радиоактивного распада характеризуется активностью радиоактивного препарата.

Активность радиоактивного препарата — число распадов, происходящих в единицу времени:

$A=\frac{\Delta N}{\Delta t}$,

где ΔN — число ядер, распавшихся за промежуток времени Δt = t − t ₀, ΔN = N ₀ − N; t ₀ — начальный момент времени, t ₀ = 0; N — число радиоактивных (нераспавшихся) ядер к моменту времени t; N ₀ — первоначальное количество радиоактивных ядер.

Активность радиоактивного изотопа:

• зависит от свойств данного радиоактивного изотопа (постоянной распада λ или периода полураспада T _1/2);
• пропорциональна числу радиоактивных ядер в данный момент времени:

A = λN, или $A=\frac{\ln 2}{T_{1/2}}N$,

где число радиоактивных ядер N определяется законом радиоактивного распада:

N = N ₀e ^{−λ t} , или $N=N_0{2}^{-\frac{t}{T_{1/2}}}$,

где λ — постоянная распада; T _1/2 — период полураспада радиоактивного элемента.

В Международной системе единиц активность радиоактивного препарата измеряется в беккерелях (1 Бк = 1 распад/с).

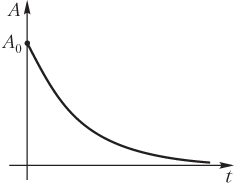
Закон изменения активности радиоактивного препарата с течением времени подобен закону радиоактивного распада:

A = A ₀e ^{−λ t} ,

где A ₀ — активность препарата в начальный момент времени t ₀ = 0, A ₀ = λN ₀; N ₀ — первоначальное количество радиоактивных ядер; A — активность препарата в момент времени t, A = λN; N — число радиоактивных ядер к моменту времени t; λ — постоянная распада (характеристика данного радиоактивного элемента).

График зависимости активности радиоактивного препарата от времени A(t) приведен на рис. 13.11.

Указанный закон может быть записан в другом виде:

$A=A_0{2}^{-\frac{t}{T_{1/2}}}$,

где A — активность препарата в момент времени t; A ₀ — активность препарата в начальный момент времени t ₀ = 0; T _1/2 — период полураспада радиоактивного элемента.